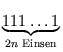
Zeige: Zieht man von einer Zahl, die aus einer geraden Anzahl von Einsen besteht
(z. B. 1111), die Zahl ab, die aus halb so vielen Zweien besteht (in diesem
Beispiel 22), so erhält man stets eine Quadratzahl (im Beispiel
1089 = 332).
Lösung:
Die Zahl, deren Dezimaldarstelleung aus genau 2n Einsen
besteht, ist gerade ein Neuntel der Zahl, die aus genauso vielen Neunen
besteht. Letztere ist aber gerade die Zahl 102n - 1.
Die Zahl, die aus 2n Einsen besteht, ist also
![]() (102n - 1).
(102n - 1).
Genauso sieht man, dass die Zahl, die aus n Zweien besteht, geschrieben
werden kann als
![]() (10n - 1).
(10n - 1).
Die gesuchte Differenz kann man deswegen folgendermaßen umschreiben:
| = | |||
| = | |||
| = |
Die Zahl in Klammern ist nun die mit genau n Dreien geschriebene natürliche Zahl.
Es gilt also stets:
 - -  = =  |
Aufgabe 2
Lisa hat ein kreisrundes Osternest gebastelt. Nun stellt sie fest, dass das
Osternest gerade so groß ist, dass sie genau acht Eier am Rand entlang
aufreihen kann. Die stehenden Eier haben einen kreisrunden Querschnitt von 4
cm Durchmesser (vgl. Skizze).
- a)
- Welchen Durchmesser hat das Osternest?
- b)
- Wenn Lisa acht Ostereier so platziert hat, passen dann noch zwei weitere Eier ins Nest (ohne zu stapeln)?
Lösung:
- a)
- Da alle Eier gleich groß sind und aneinandergereiht sind, bilden die
Mittelpunkte der Querschnitte ein regelmäßiges Achteck. Sei M der
Mittelpunkt des Osternestes und seien A und B die Mittelpunkte zweier
aneinandergrenzender Ostereier (vgl. Skizze). Sei r der Radius eines Eies.
Sei P der in der Skizze eingezeichnete Berührpunkt zweier Kreise und a der Abstand von M zu P. Der Zeichnung kann man die Beziehung a = r + y entnehmen, wobei y die Länge der Seite AN im gleichschenklig rechtwinkligen Dreieck ABN ist. Es gilt also y =
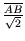 =
= 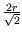 =
= 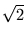 . r und
deswegen
. r und
deswegen
a = r + y = r + 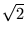 . r = (1 +
. r = (1 + 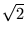 ) . r.
) . r.
Nun kann man im rechtwinkligen Dreieck AMP den Satz des Pythagoras anwenden und findet:x = 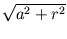 =
= 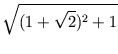 . r =
. r = 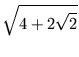 . r.
. r.
Also ist der Durchmesser d des Osternestes:d = 2x + 2r =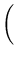 2
2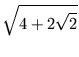 + 2
+ 2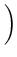 . 2 cm
. 2 cm
Der Durchmesser ist ungefähr d
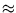 14, 45 cm.
14, 45 cm.
- b)
- Im Folgenden zeigen wir, dass jedes weitere Ei, das in das Osternest gelegt
wird, den Mittelpunkt des Osternestes überdeckt. Dadurch ist gezeigt, dass
keine zwei weiteren Eier mehr ins Nest gelegt werden können.
Ein weiteres Ei liegt möglichst weit vom Mittelpunkt des Nestes entfernt, wenn es wie in Skizze 3 platziert ist (das Ei mit Mittelpunkt Q). Das Dreieck ABQ ist nun ein gleichseitiges Dreieck mit Seitenlänge 2r. Ist R die Mitte der Strecke AB, so ist QR die Höhe des Dreiecks und damit gilt:
Nach Teil a) ist MA = x =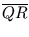 =
= 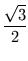 . 2r =
. 2r = 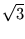 . r.
. r.
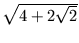 . r und nach dem Satz
des Pythagoras im Dreieck ARM ist:
. r und nach dem Satz
des Pythagoras im Dreieck ARM ist:
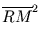
= 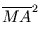 -
- 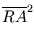
= 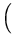 4 + 2
4 + 2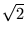
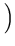 . r2 - r2
. r2 - r2= 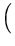 3 + 2
3 + 2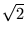
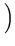 . r2
. r2
Und damit:
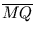
= 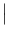
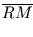 -
- 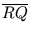
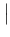 =
= 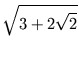 . r -
. r - 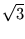 . r
. r= 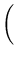
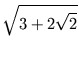 -
- 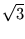
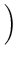 . r
. r
Damit der Mittelpunkt M ,,im Ei liegt``, muss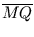 < 1 . r
gelten. Diesen Nachweis bekommt man durch Äquivalenzumformung der Ungleichung:
< 1 . r
gelten. Diesen Nachweis bekommt man durch Äquivalenzumformung der Ungleichung:
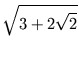 -
- 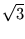
< 1 
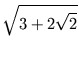
< 1 + 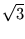 (Quadrieren1)
(Quadrieren1) 3 + 2
3 + 2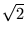
< 1 + 2 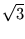 + 3
+ 3 2
2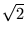
< 1 + 2 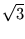
Die letzte Ungleichung ist offensichtlich erfüllt.Bemerkung: Traut man dem Taschenrechner eine gewisse Genauigkeit zu (Achtung: Diese Vorgehensweise ist mathematisch nicht ganz korrekt, da Rundungsfehler das Ergebnis verfälschen könnten), so ist:
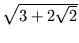 -
- 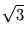
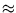 0, 68 < 1 .
0, 68 < 1 .
Aufgabe 3
Zu Ostern möchte Ferdinand Ostereier bemalen. Dazu hat er fünf verschiedene
Farben: Rot, Grün, Gelb, Orange und Blau. Damit die Eier auch schön bunt
werden, bemalt Ferdinand jedes Ei mit genau drei Farben.
- a)
- Wie viele verschiedene Farbkombinationen sind möglich?
- b)
- Zeige, dass es unter sieben bemalten Eiern immer drei gibt, die in mindestens zwei Farben übereinstimmen.
Lösung:
- a)
- Hier muss man also die Anzahl der Möglichkeiten zählen, aus den
fünf gegebenen Farben drei verschiedene auszuwählen.
Für die erste Farbe hat man fünf Möglichkeiten, für die zweite vier und für die dritte dann noch drei Möglichkeiten. Das sind zusammen 5 . 4 . 3 = 60 Möglichkeiten. Dabei wird aber jede Kombination sechsmal gezählt, nämlich in jeder der sechs möglichen Anordnungen dreier Farben.
Daher gibt es genau 10 Farbkombinationen.
Etwas kürzer kann man auch direkt benutzen, dass die gesuchte Anzahl entsprechend der Definition des Binomialkoeffizienten gerade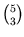 = 10 ist.
= 10 ist.
- b)
- (Lösung von Jannis Klaus, Klasse 9)
Es gibt zehn mögliche verschiedene Farbenpaare unter den fünf Farben. Auf einem Ei sind stets drei verschiedene Farbenpaare vertreten, auf sieben Eiern insgesamt also 21 Farbenpaare.
Da es aber nur zehn verschiedene gibt, muss nach Schubfachprinzip eines der Paare mindestens dreimal vorkommen. Da jedes Ei mit drei verschiedenen Farben bemalt ist, liegen diese Paare auf drei unterschiedlichen Eiern. Es gibt also drei Eier, die in wenigstens zwei Farben übereinstimmen.
Aufgabe 4
Firma Superei stellt Sicherheits-Eier her, die Stürze
aus größeren Höhen überstehen. Die Firma hat nun zwei Probe-Eier nach
einem neuen Verfahren hergestellt und möchte ihre Stabilität testen. Dazu
werden die Eier aus verschiedenen Stockwerken ihres 20-stöckigen
Firmengebäudes fallen gelassen. Wie viele Versuche
werden maximal gebraucht, um festzustellen, bis zu welcher Höhe genau (in
Stockwerken) ein Ei einen Sturz auf das Pflaster übersteht? Bedenke: Wenn ein
Ei einen Sturz überstanden hat, kann es für einen weiteren Versuch verwendet
werden, sonst natürlich nicht. Am Ende dürfen beide Eier kaputt sein.
Wem das zu einfach sein sollte: Wie viele Versuche sind es maximal, wenn die Firma gleich drei (oder noch mehr) Probe-Eier herstellt?
Lösung:
Wir lösen die Aufgabe gleich ganz allgemein, indem wir bestimmen, wie viele
Stockwerke (bzw. Stabilitätsgrade von Eiern) man mit einer gegebenen Zahl von
Probe-Eiern und einer gegebenen Zahl von Versuchen
auseinanderhalten kann. Diese Zahl bezeichnen wir mit s(v, e); dabei steht v
für die Anzahl der Versuche, e für die Anzahl der Probe-Eier.
Wenn man nur ein Ei zur Verfügung hat, ist die Antwort einfach, da das Ei ja erst kaputtgehen darf, wenn man schon weiß, dass es beim Fall aus dem direkt darunterliegenden Stockwerk nicht kaputtgeht. Also muss man beim ersten Stockwerk anfangen; wenn es heil bleibt, versucht man es mit den zweiten Stockwerk usw. Damit kommt man mit v Versuchen bis zum v-ten Stockwerk, es gilt also
Hat man mehr als ein Ei und mehr als einen Versuch, startet man in einem (noch zu bestimmenden) Stockwerk n. Bleibt das Ei heil, weiß man, dass es auch bei Würfen von den darunterliegenden Stockwerken heil bleibt. Man muss demnach nur noch oberhalb des n-ten Stockwerkes suchen. Dafür hat man nach wie vor e Eier und einen Versuch weniger zur Verfügung.
Geht das Ei kaputt, muss man in den Stockwerken unter dem n-ten suchen und hat dafür sowohl ein Ei als auch einen Versuch weniger. Es ist also für e, v > 1:
| Eier | ||||||||||
| Versuche | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 4 | 4 | 10 | 14 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| 5 | 5 | 15 | 25 | 30 | 31 | 31 | 31 | 31 | 31 | 31 |
| 6 | 6 | 21 | 41 | 56 | 62 | 63 | 63 | 63 | 63 | 63 |
| 7 | 7 | 28 | 63 | 98 | 119 | 126 | 127 | 127 | 127 | 127 |
| 8 | 8 | 36 | 92 | 162 | 218 | 246 | 254 | 255 | 255 | 255 |
| 9 | 9 | 45 | 129 | 255 | 381 | 465 | 501 | 510 | 511 | 511 |
| 10 | 10 | 55 | 175 | 385 | 637 | 847 | 967 | 1012 | 1022 | 1023 |
Daraus ergibt sich, dass man für 20 Stockwerke und zwei Eier maximal sechs Versuche benötigt. Hat man drei Eier, braucht man nur höchstens fünf Versuche.
Mit ein wenig Überlegung kann man aus der Tabelle auch entnehmen, wie man im konkreten Fall vorgehen muss, um die Belastbarkeit zu ermitteln. In unserem Fall muss der erste Versuch im 5. oder 6. Stockwerk erfolgen, denn es muss ein Stockwerk im Intervall [20 - s(5, 2), s(5, 1) + 1] sein, damit man mit den restlichen Versuchen noch in jedem Fall auskommt.
Zum Beispiel kann man nach folgendem Schema vorgehen, links für zwei, rechts
für drei Eier (Zu deuten ist das Schema
so: bleibt das Ei heil, muss man beim folgenden Versuch in das nächsthöher
gelegene Stockwerk der folgenden Spalte gehen, ansonsten - sofern man noch
nicht die Lösung hat - zum nächstniedriger
gelegenen. [Diese Darstellung ist der Lösung von Helmut Grohne entlehnt.]):
| Mit 2 Eiern: | ||||||
| Stock- | Versuch | |||||
| werk | 1. | 2. | 3. | 4. | 5. | 6. |
| 20 | X | |||||
| 19 | X | |||||
| 18 | X | |||||
| 17 | X | |||||
| 16 | X | |||||
| 15 | X | |||||
| 14 | X | |||||
| 13 | X | |||||
| 12 | X | |||||
| 11 | X | |||||
| 10 | X | |||||
| 9 | X | |||||
| 8 | X | |||||
| 7 | X | |||||
| 6 | X | |||||
| 5 | X | |||||
| 4 | X | |||||
| 3 | X | |||||
| 2 | X | |||||
| 1 | X | |||||
| Mit 3 Eiern: | |||||
| Stock- | Versuch | ||||
| werk | 1. | 2. | 3. | 4. | 5. |
| 20 | X | ||||
| 19 | X | ||||
| 18 | X | ||||
| 17 | X | ||||
| 16 | X | ||||
| 15 | X | ||||
| 14 | X | ||||
| 13 | X | ||||
| 12 | X | ||||
| 11 | X | ||||
| 10 | X | ||||
| 9 | X | ||||
| 8 | X | ||||
| 7 | X | ||||
| 6 | X | ||||
| 5 | X | ||||
| 4 | X | ||||
| 3 | X | ||||
| 2 | X | ||||
| 1 | X | ||||
Dass oberhalb der Diagonale in der Tabelle der Werte s(v, e) Zweierpotenzen weniger eins stehen, ist übrigens kein Zufall: Wenn man mehr Eier als Versuche hat, ist man nicht mehr durch die Nebenbedingung des möglichen Verlusts von Eiern beeinflusst. Dann kann man die Suche so gestalten, dass man immer v-mal probieren muss, bis man zu einem Ergebnis kommt. Den 2v möglichen Ausgängen dieser Versuche entsprechen die 2v möglichen Ergebnisse ,,Ei hält keinen Sturz aus``, ,,Ei hält Sturz bis genau zum 1. Stockwerk aus`` usw. bis ,,Ei hält Sturz bis genau zum (2v - 1)-ten Stockwerk aus``.
Man kann sogar eine geschlossene Formel für die Einträge in der Tabelle angeben, ohne dass wir sie hier beweisen wollen. Sie lautet:
Fußnoten
- ...
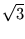 1
1 - Im Allgemeinen ist Quadrieren keine Äquivalenzrelation
(
(- 1)2 = 12, aber -1
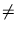 1)!
Hier rechnen wir aber nur mit positiven Zahlen.
1)!
Hier rechnen wir aber nur mit positiven Zahlen.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File

![\includegraphics[width=3cm]{osternest.eps}](img13.png)
![\includegraphics[width=4.5cm]{osternestloes3.eps}](img24.png)
![\includegraphics[width=4.5cm]{osternestloes2.eps}](img25.png)