Beispiellösungen zu Aufgabenblatt 1

aktualisiert: 18. April 2000

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1



Herr Schulze fährt jeden Tag per Bahn zur Arbeit in die Stadt und kehrt jeden Abend mit demselben Zug zurück, der um 17 Uhr ankommt. Dort am Bahnhof kommt jeden Tag zu genau dieser Zeit auch Herrn Schulzes Chauffeur an, um ihn sofort abzuholen und wieder nach Hause zu fahren.
Eines schönen Tages nimmt Herr Schulze nun einen früheren Zug, der schon um 16 Uhr ankommt. Weil er nicht warten will, geht er seinem Chauffeur entgegen und trifft diesen auch unterwegs, steigt ein, fährt mit ihm nach Hause und kommt dort 20 Minuten früher an als gewöhnlich.
Eines anderen schönen Tages nimmt Herr Schulze einen anderen früheren Zug, der um 16.30 Uhr ankommt. Genau wie beim letzten Mal läuft er seinem Chauffeur schon entgegen, trifft ihn, steigt ein und kommt wieder früher als gewöhnlich zu Hause an. Wieviel früher?
(Bemerkung: Es wird natürlich vorausgesetzt, dass sowohl der Chauffeur als auch Herr Schulze stets mit derselben konstanten Geschwindigkeit fahren bzw. laufen.)



Behauptung: Herr Schulze kommt unter den gegebenen Voraussetzungen genau 10 Minuten früher an als gewöhnlich!


Erster Beweis (rechnerisch): In der ersten Situation kommen die beiden 20 Minuten früher an, also hat der Chauffeur auf jedem seiner beiden Fahrwege (hin und zurück) genau 10 Minuten gespart. Insbesondere trifft er Herrn Schulze schon um 16.50 Uhr. Herr Schulze ist also in den 50 Minuten ab 16.00 Uhr genau den Weg gelaufen, den der Chauffeur in 10 Minuten gefahren wäre. Daraus folgt aber, dass der Chauffeur 5-mal so schnell ist wie Herr Schulze.
In der zweiten Situation, in der Herr Schulze 30 Minuten früher ankommt, treffen sich die beiden t Minuten vor 17.00 Uhr irgendwo zwischen Bahnhof und zu Hause. Herr Schulze läuft also 30 - t Minuten. Da er 5-mal so langsam ist wie der Chauffeur, gilt

30 - t = 5t     $\displaystyle \Rightarrow$    t = 5    

Der Chauffeur spart auf jedem Weg 5 Minuten, Herr Schulze kommt also 10 Minuten früher an.


Zweiter Beweis (grafisch): Man kann sich die Bewegungen von Herrn Schulze und seinem Chauffeur in einem sogenannten Weltliniendiagramm veranschaulichen. Dieses ist ein Koordinatensystem, auf dessen x-Achse die Zeit und auf dessen y-Achse der Ort eingetragen wird. Für eine Bewegung kann man nun zu jeder Zeit den Ort feststellen und man erhält eine Kurve. Bei Bewegungen mit konstanter Geschwindigkeit sind dies Geraden. Je schneller eine solche Bewegung verläuft, umso steiler verlaufen die Geraden. In Abbildung [*] sind die Weltlinien von Herrn Schulze und seinem Chauffeur dargestellt. Im Normalfall fährt der Chauffeur bei O los, trifft am Bahnhof bei B1 auf Herrn Schulze und fährt nach A1 zurück. In den beiden speziellen Situationen trifft Herr Schulze schon bei B3 bzw. B2 am Bahnhof ein, läuft los, begegnet dem Chauffeur bei C3 bzw. C2 und kommt dementsprechend bei A3 bzw. A2 zu Hause an. Da sich Herr Schulze und sein Chauffeur stets mit der gleichen Geschwindigkeit bewegen, sind ihre Weltlinien parallel, also B3C3 || B2C2 und B1A1 || C2A2 || C3A3. Nach Voraussetzung ist nun $ \overline{{B_3B_2}}$ = $ \overline{{B_2B_1}}$. Daraus folgt dann nach Strahlensatz auch $ \overline{{C_3C_2}}$ = $ \overline{{C_2B_1}}$ und hieraus ebenfalls nach Strahlensatz $ \overline{{A_3A_2}}$ = $ \overline{{A_2A_1}}$. Da aber der Strecke A3A1 nach Voraussetzung 20 Minuten entsprechen, entspricht der Strecke A2A1 genau die Hälfte, also 10 Minuten. Das war zu zeigen.



\includegraphics[width=\textwidth]{loes01a}

-.5cm 23.5cm

Aufgabe 2



Eine Schokoladentafel einer bekannten Marke besteht aus 4×4 quadratischen Stücken. Sie soll unter 16 Personen aufgeteilt werden, so dass jeder genau ein solches Quadrat bekommt. Dazu muss die Schokolade natürlich in die kleinen Teile zerbrochen werden. Dies soll nun folgendermaßen geschehen: Man nimmt einen vorhandenen Teil der Schokolade, der noch aus mehr als einem einzelnen Quadrat besteht, und macht einen beliebigen Schnitt entlang der Quadratkanten, so dass der Teil in zwei Teile auseinanderbricht. Eine Möglichkeit für den ersten Schnitt wäre also folgende:

\includegraphics[width=10cm]{schoko}

Für das Auseinanderbrechen hat man nun eine Reihe von Möglichkeiten. Wieviel Schnitte muss man dabei mindestens machen? Man versuche die Antwort zu begründen!



Die Lösung stammt von Julian Vogel aus dem Felix-Klein-Gymnasium in Göttingen:
,, Bei jeder Teilung wird das Schokoladenstück, das gerade geteilt wird, in zwei Teile geteilt. Nach einem Schnitt gibt es also genau 1 Schokoladenteil mehr als vorher. Will man also aus dem anfangs vorhandenen Schokoladenteil 16 machen, so ist 15-mal eine Erhöhung der Anzahl um 1 nötig, es muss also genau 15-mal geschnitten werden.``
Noch eine Anmerkung: Für die Lösung der Aufgabe war es (wie bei vielen Aufgaben) entscheidend, den Aufgabentext genau zu lesen und dabei zu verstehen, was mit einem ,,Schnitt`` gemeint ist. Dort stand, dass bei einem Schnitt immer ein Teil genommen wird und in zwei Teile zerbrochen wird, deshalb hat man nach jedem Schnitt genau ein Teil mehr. Es ist also völlig egal, wie man schneidet und welche Form die Schnitte haben, man braucht immer genau 15 Schnitte. Es geht nicht mit weniger, aber auch nicht mit mehr.



Aufgabe 3



Es gibt Zahlen, die sich nicht ändern, wenn man sie rückwärts liest. So sind zum Beispiel 52325 und 88 oder natürlich auch 3 solche sogenannten Spiegelzahlen oder Palindrome. Schreibt man alle Palindrome auf, die kleiner als 150 sind, so sieht die Liste folgendermaßen aus:

1, 2, 3, 4, 5, 6, 7, 8, 9
11, 22, 33, 44, 55, 66, 77, 88, 99
101, 111, 121, 131, 141

Dies sind genau 23 Stück. Mit P(N) sei nun die Anzahl aller Palindrome bezeichnet, die kleiner oder gleich N sind. Also ist zum Beispiel P(11) = 10 und P(150) = 23. Man versuche eine Formel für P(N) zu finden und berechne P(1234567890)! Außerdem zeige man, dass stets P(N) > 2$ \sqrt{{N}}$ - 3 gilt!



Lösung: Zunächst einmal gibt es zwei Möglichkeiten, Palindrome zu erzeugen.
Variante 1: Man kann sich m Stück unter den Ziffern 0, 1, ..., 9 wählen (durchaus auch einige mehrfach oder gar nicht) und diese dann in umgekehrter Reihenfolge noch einmal hinten anfügen. Hierbei sind führende Nullen zu streichen; hat man also etwa für m = 3 die Ziffern 014 gewählt, so wird daraus 1441, nicht etwa 014410 (=14410, was ja kein Palindrom wäre). Somit entstehen hierbei alle Palindrome mit einer geraden Stellenzahl, die kleiner oder gleich 2m ist.
Variante 2: Man wählt sich m Ziffern und fügt an die m-te die (m - 1)-te, dann die (m - 2)-te usw. bis zur ersten noch einmal an (wiederum ohne führende Nullen). Hierbei entstehen alle Palindrome mit einer ungeraden Stellenzahl, die kleiner oder gleich 2m - 1 ist.

Abbildung: Variante 1

\includegraphics[width=9cm]{loes01b.eps}
Abbildung: Variante 2
\includegraphics[width=9cm]{loes01c.eps}

Man habe nun eine Zahl N mit n Stellen gegeben und außerdem sei zunächst n = 2k eine gerade Zahl. Nach Variante 2 kann man dann mit m = k alle Palindrome mit ungerader Stellenzahl kleiner oder gleich N erzeugen. Hierzu wählt man sich wie beschrieben k-mal eine der 10 Ziffern. Dazu hat man genau
  $\displaystyle \underbrace{{10\cdot 10 \cdot \ldots \cdot 10}}\,$ = 10k  
  k-mal    

Möglichkeiten. Die Null, die hierbei auch als Palindrom entsteht, soll dabei nicht mitgezählt werden (ist keine natürliche Zahl), also ist die Anzahl U(N) dieser ungeradzahlstelligen Palindrome

U(N) = 10k - 1.    

Nun fehlen noch die Palindrome mit gerader Stellenzahl. Diese werden nach Variante 1 mit m = k erzeugt. Man muss hierbei jedoch aufpassen, dass die entstehenden Palindrome kleiner bleiben als N. Dies ist auf jeden Fall dann der Fall, wenn die aus den ersten m Ziffern von N gebildete Zahl $ \hat{{N}}$ größer ist als die Zahl Z, die aus den bei Variante 1 gewählten m Ziffern gebildet wird. Für die Wahl dieser Ziffern (bzw. der Zahl Z) hat man also hier

G(N) = $\displaystyle \hat{{N}}$ - 1    

Möglichkeiten. Bilden die gewählten m Ziffern genau die Zahl $ \hat{{N}}$, so muss man schauen, ob das entstehende Palindrom wirklich kleiner als N ist. Ist zum Beispiel N = 1947, so hat man $ \hat{{N}}$ = 19 und das zu dieser Ziffernwahl gehörige Palindrom 1991. Dieses dürfte nicht mitgezählt werden, da es größer als N ist. Für N = 1999 hingegen ist ebenfalls $ \hat{{N}}$ = 19, und weil 1991 $ \leq$ 1999, wird dieses Palindrom noch mitgezählt. Je nachdem, ob dieses bei dem gegebenen N klappt oder nicht, muss man also noch ein Palindrom mehr zählen oder nicht. Man setzt hierfür V(N) = 1, wenn es klappt, oder V(N) = 0 sonst (,,V`` steht für ,,vielleicht noch eines``). Zusammen ergibt dies dann

P(N) = U(N) + G(N) + V(N) = 10k - 1 + $\displaystyle \hat{{N}}$ - 1 + V(N). (1)

Genauso geht man vor, wenn N eine ungerade Stellenzahl n = 2k + 1 hat. Dann gibt es von den geradzahlstelligen Palindromen kleiner als N gerade G(N) = 10k - 1 Stück (gebildet nach Variante 1 mit m = k). Bei den Palindromen ungerader Stellenzahl gebildet nach Variante 2 (mit m = k + 1) muss man wieder aufpassen, dass die aus den ersten (k + 1) Stellen von N gebildete Zahl $ \hat{{N}}$ größer ist als die aus den gewählten Ziffern gebildete Zahl Z, also U(N) = $ \hat{{N}}$ - 1. Ebenso hat man wieder das V(N). Zusammen ergibt sich genau wieder Formel ([*]). Damit ist man eigentlich fertig.


Um nun noch die beiden Fälle (n gerade oder ungerade) unter einen Hut zu bringen, kann man die sogenannte Gaußklammer-Funktion $ \lfloor$.$ \rfloor$ benutzen. Bei positiven Zahlen tut sie nichts weiter, als alle Nachkommastellen zu streichen, wie zum Beispiel $ \lfloor$2, 31$ \rfloor$ = 2, $ \lfloor$9, 9$ \rfloor$ = 9 oder $ \lfloor$6$ \rfloor$ = 6.
Unter anderem gilt dann für n = 2k und n = 2k + 1:

$\displaystyle \lfloor$$\displaystyle {\frac{{n}}{{2}}}$$\displaystyle \rfloor$ = k.    

Um $ \hat{{N}}$ zu erhalten, muss man in beiden Fällen die letzten k Stellen der Zahl N streichen. Dies gelingt durch

$\displaystyle \hat{{N}}$ = $\displaystyle \lfloor$$\displaystyle {\frac{{N}}{{10^k}}}$$\displaystyle \rfloor$.    

(Zum Beispiel ist bei N = 1943 die Zahl k = 2, also $ {\frac{{N}}{{10^2}}}$ = 19, 43. Das heißt aber $ \lfloor$$ {\frac{{N}}{{10^k}}}$$ \rfloor$ = $ \lfloor$19, 43$ \rfloor$ = 19 = $ \hat{{N}}$.) Setzt man diese beiden Ergebnisse noch in Gleichung ([*]) ein, so bekommt man die für alle N gültige Formel1

P(N) = 10$\scriptstyle \lfloor$$\scriptstyle {\frac{{n}}{{2}}}$$\scriptstyle \rfloor$ + $\displaystyle \lfloor$$\displaystyle {\frac{{N}}{{10^{\lfloor\frac{n}{2}\rfloor}}}}$$\displaystyle \rfloor$ - 2 + V(N).    

Hiermit kann man nun rechnen, zum Beispiel P(150) = 10 + 15 - 2 + 0 = 23 wie in der Aufgabe angegeben. Oder aber auch P(1234567890) = 105 + 12345 - 2 + 1 = 112344. Um die geforderte Ungleichung zu beweisen kann man nun $ \lfloor$x$ \rfloor$ > x - 1 benutzen. Damit gilt nämlich
P(N) = 10$\scriptstyle \lfloor$$\scriptstyle {\frac{{n}}{{2}}}$$\scriptstyle \rfloor$ + $\displaystyle \lfloor$$\displaystyle {\frac{{N}}{{10^{\lfloor\frac{n}{2}\rfloor}}}}$$\displaystyle \rfloor$ - 2 + V(N)  
  > 10$\scriptstyle \lfloor$$\scriptstyle {\frac{{n}}{{2}}}$$\scriptstyle \rfloor$ + $\displaystyle {\frac{{N}}{{10^{\lfloor\frac{n}{2}\rfloor}}}}$ - 3 + V(N)  
  $\displaystyle \geq$ 10$\scriptstyle \lfloor$$\scriptstyle {\frac{{n}}{{2}}}$$\scriptstyle \rfloor$ + $\displaystyle {\frac{{N}}{{10^{\lfloor\frac{n}{2}\rfloor}}}}$ - 3  
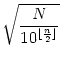  = $\displaystyle \left(\vphantom{\sqrt{10^{\lfloor\frac{n}{2}\rfloor}} - \sqrt{ \frac{N}{10^{\lfloor\frac{n}{2}\rfloor}} }}\right.$$\displaystyle \sqrt{{10^{\lfloor\frac{n}{2}\rfloor}}}$ - $\displaystyle \sqrt{{ \frac{N}{10^{\lfloor\frac{n}{2}\rfloor}} }}$$\displaystyle \left.\vphantom{\sqrt{10^{\lfloor\frac{n}{2}\rfloor}} - \sqrt{ \frac{N}{10^{\lfloor\frac{n}{2}\rfloor}} }}\right)^{2}_{}$ + 2$\displaystyle \sqrt{{N}}$ - 3  
  $\displaystyle \geq$ 2$\displaystyle \sqrt{{N}}$ - 3  

Das war zu zeigen. Ein genauerer Vergleich der beiden Funktionen zeigt, dass sie sich an unendlich vielen Stellen N sehr nahe kommen, nämlich an allen Zahlen N = 9999...998 mit einer geraden Anzahl von Stellen. Dies kann man auch anhand obiger Abschätzung beweisen.
Abbildung: Vergleich von P(N) mit 2$ \sqrt{{N}}$ - 3
\includegraphics[width=10cm]{loes01d.eps}



Aufgabe 4



Familie Wurm (Papa, Mama, Kind) hat ein Problem: die Bettdecke von Kindwurm hat einen Riss, und es muss eine neue angeschafft werden. Die Decke soll natürlich die Eigenschaft haben, dass, egal wie sich Kindwurm mit seiner stolzen Länge von genau einem Meter auch räkelt, Kindwurm mit ihr zugedeckt werden kann.

Eine solche Decke könnte zum Beispiel die Form eines Kreises mit Durchmesser 2 m haben (siehe Bildchen). Denn egal wie Würmchen auch liegt, legt man den Mittelpunkt dieser Decke auf Würmchens eines Ende, so bleibt Wurm vollständig unter der Decke (er ist ja genau einen Meter lang, also so lang wie der Radius der Decke!). \includegraphics[height=30mm]{wurm}



Damit wäre das Problem der Familie Wurm gelöst, wenn nicht Bettdeckenstoff im Wurmland so unglaublich teuer wäre. Langer Rede kurzer Sinn: Familie Wurm will eine Decke mit möglichst kleiner Fläche! Obige Decke hätte nun eine Fläche von ungefähr 3, 141593 m2. Kann man das noch verbessern? Jeder Quadratmillimeter zählt, also lohnt es sich, nach kleineren Decken zu suchen! Man versuche eine möglichst kleine Decke zu finden, die aber immer noch Würmchen in jeder Lage abdeckt!



PS: Eine optimale Lösung ist wohl noch nicht bekannt, allerdings ist es nicht allzu schwer, bessere Decken als obige zu finden.



Lösung: Vorweg: Einige von euch haben den Vorschlag gemacht, für Kindwurm einen Schlafsack zu nähen. Ein Wurm ist ja recht dünn (sagen wir mal, er habe einen kreisförmigen Querschnitt mit Radius r), und ein zylinderförmiger Schlafsack hat ja nur eine Oberfläche von 2$ \pi$r (Einheiten wie m2 werden hier der Einfachheit halber meist weggelassen). Selbst für r = 0, 1 (dann wäre Würmchen schon ziemlich dick) wären das nur 0, 2 . $ \pi$, also nur ein Fünftel unseres Vorschlages. Wenn man aber so anfängt, muss man auch bedenken, dass der Schlauch an einem Ende geschlossen werden muss, was noch etwas mehr Stoff sowie mehr Nähgeschick erfordert, außerdem ist das Hineinkriechen recht unangenehm, Reißverschlüsse sind jedoch fast unerschwinglich ...Und schließlich ist Deckenstoff im Wurmland deswegen so teuer, weil es ein besonders gut warm haltender Stoff ist (für Wurmkinder sogar gesetzlich vorgeschrieben), der allerdings den Nachteil hat, dass er sich sehr schlecht biegen lässt. (Man hätte ja sonst auch einen recht dünnen Streifen Stoff von einem Meter Länge nehmen und ihn so zurechtbiegen können, dass er die Form der Wurms nachvollzieht. Da wir den Wurm als vernachlässigbar dünn annehmen wollen, bräuchte man also im Prinzip gar keinen Stoff!)
So war das natürlich nicht gemeint, und fast alle haben das ja auch erkannt. Die meisten von euch haben auch die naheliegendste recht gute Lösung angegeben:

Abbildung: Decke mit r = 1/2
41mm
\includegraphics[height=24mm]{loewu1}
Eine Kreisscheibe mit Radius 1/2 reicht ebenfalls aus, um Kindwurm zu bedecken . Das sieht man am besten folgendermaßen ein: Wenn man die Decke so auf den Wurm legt, dass ihr Mittelpunkt auf der Mitte des Wurms zu liegen kommt, so ist kein Punkt des Wurms mehr als einen halben Meter von diesem Mittelpunkt entfernt, daher liegt er vollständig innerhalb der Kreisscheibe (bzw. ggf. auf deren Rand, der aber zur Kreisscheibe gehören soll). Leider haben viele von euch nicht begründet, warum man Kindwurm mit so einer Decke in jedem Fall zudecken kann; das hätte zur Lösung natürlich eigentlich dazugehört. Das Ergebnis ist auf jeden Fall, dass man für diese Decke nur (1/2)2 . $ \pi$ m2 $ \approx$ 0, 785 m2 Stoff benötigt, also nur ein Viertel im Vergleich zu der von uns angegebenen Decke.

Will man noch bessere Ergebnisse erzielen, muss man mehr Überlegungen anstellen. Auf den Bildern [*] und [*] seht ihr mögliche andere Deckenformen.

Abbildung: Ein Wurmende fest
43mm
\includegraphics[height=23.4mm]{loewu2}
Man kann sich den Wurm (nur gedanklich!) in einzelne Abschnitte unterteilen und sich überlegen, welche Form man braucht, um einen dieser Abschnitte bei einer vorgegebenen Lage der beiden oder eines Endpunkte(s) zu überdecken. Der Fall, dass man die Lage nur eines Endpunktes als fix betrachtet, ist oben bzw. auf dem Aufgabenblatt schon gelöst worden: Geht von einem Punkt A ein Wurmstück der Länge l aus, so liegt dieses garantiert vollständig in einer Kreisscheibe um A mit dem Radius l.

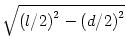Etwas kniffliger wird es, wenn man die Lage beider Endpunkte A und B, die einen Abstand d voneinander haben mögen, gegeben hat: Dann liegt das Wurmstück (wieder mit der Länge l) garantiert in einer Ellipsenscheibe mit den Brennpunkten A und B und mit großer Halbachse l /2. Daraus ergibt sich nach Pythagoras eine kleine Halbachse der Länge $ \sqrt{{\left(l/2\right)^2-\left(d/2\right)^2}}$. Mit diesem Wert lässt sich nicht mehr so schön rechnen, aber für unsere Abschätzungen reicht es zu wissen, dass die kleine Halbachse nicht länger als l /2 ist. Man denke sich nun die Punkte des Wurmes bei einem Viertel (A) sowie bei drei Vierteln (B) seiner Länge markiert und lege den Wurm so auf eine gegebene Achse, dass A auf dem (selbst gewählten) Nullpunkt der Achse liegt, B rechts davon ebenfalls auf der Achse.

Abbildung: Beide Wurmenden fest
\includegraphics[height=25mm]{loewu3}
Abbildung: Wurm bei 1/4 und 3/4 fest
\includegraphics[height=24mm]{loewu4}
Dann liegt der Wurm garantiert in der Figur, die durch die Überlagerung zweier Kreisscheiben mit Radius 1/4 um A und B sowie der Ellipsenscheibe mit den Brennpunkten A und B und der großen Halbachse 1/4 entsteht. Man beachte, dass die Ellipse rechts und links nicht aus den Kreisscheiben ,,herausstoßen`` kann, da ihr Mittelpunkt zwischen A und B liegt und die große Halbachse nur genauso groß wie die Kreisradien ist. Ebenso liegt kein Punkt der Ellipse weiter als 1/4 von der Achse entfernt, weil die kleine Halbachse kleiner oder gleich 1/4 ist. In den beiden Extremfällen sind A und B gleich bzw. liegen im Abstand von 1/2 zueinander.

Abbildung: Decke mit A $ \approx$ 0, 446
50mm
\includegraphics[height=25mm]{loewu5}

Das bedeutet aber, dass man den Wurm, egal wie er sich gekrümmt hat, vollständig von der Figur in Abbildung [*] bedecken kann, da in ihr alle möglichen oben konstruierten Kreis-Ellipse-Kreis-Gebilde (also für jeden möglichen Abstand zwischen A und B) enthalten sind: Ein Quadrat mit der Seitenlänge 1/2, daran anliegend an zwei gegenüberliegenden Seiten je ein Halbkreis mit Radius 1/4. Der Flächeninhalt dieser Figur beträgt $ \left(\vphantom{ 0,5 }\right.$0, 5$ \left.\vphantom{ 0,5 }\right)^{2}_{}$ + 2 . 0, 5 . $ \pi$$ \left(\vphantom{ 0,25 }\right.$0, 25$ \left.\vphantom{ 0,25 }\right)^{2}_{}$ $ \approx$ 0, 446, was noch deutlich besser ist als der kleinere Kreis. Bis zu welcher Länge der kleinen Halbachse (bei großer Halbachse 1/2) eine reine Ellipsenform eine mögliche Lösung ist, ist uns nicht bekannt. Zumindest geht es noch für 0, 319, weil dann noch der unten vorgestellte Halbkreis in der Figur enthalten ist. Ein Vorschlag eines Teilnehmers war, für die kleine Halbachse die Länge 1/(2$ \pi$)( $ \approx$ 0, 159) zu nehmen. (In diese Ellipse würde der Wurm immerhin genau hineinpassen, wenn er sich zu einem Kreis rollt.) Wer Lust hat, kann versuchen, sich zu überlegen, dass dies zu klein ist. (Tipp: Der Wurm kann nicht überdeckt werden, wenn er sich zu einem rechten Winkel mit zwei Schenkeln der Länge 1/2 legt.)
Die beste uns bekannte Lösung ist genau halb so groß wie der Kreis mit Radius 1/2, es ist nämlich genau ein Halbkreis davon. Der Beweis, dass dies reicht, benutzt wie oben die Prinzipien der Kreis- bzw. der Ellipsenscheibe.

Abbildung: Kleinste uns bekannte Decke, A $ \approx$ 0, 393
65mm
\includegraphics[height=21mm]{loewu6}

Eine Gerade, die den Wurm berührt, aber nicht schneidet, heiße Stützgerade. Wenn es nur Stützgeraden gibt, die den Wurm in genau einem Punkt berühren, so liegt dieser in der Form einer konvexen Schleife mit eventuell zusätzlich nach innen hin liegenden Abschnitten, also mit einem Umfang kleiner gleich 1. Man wähle sich eine der Stützgeraden aus, und der Berührpunkt heiße K. Jeder Punkt des Wurms hat einen Abstand von kleiner oder gleich 1/2 von K. (Man kann sich einem Punkt auf dem Rand ja nach Belieben von beiden Seiten nähern und den kürzeren Weg wählen; für innere Punkte ist die Aussage dann klar.) Damit liegt Kindwurm in einem Kreis um K mit Radius 1/2. Da er aber vollständig auf einer Seite der Geraden liegt, liegt er auch in einem Halbkreis mit Radius 1/2.
Wenn der eben behandelte Fall nicht eintritt, gibt es eine Stützgerade g, die den Wurm in zwei Punkten P und Q (und eventuell noch weiteren) berührt. Diese teilen ihn der Reihe nach in drei Teilstücke A, B und C mit den Längen a, b und c (mit a + b + c = 1) ein. Der Abstand d zwischen P und Q ist offensichtlich d$ \le$b. Den oben durchgeführten Überlegungen entsprechend liegt A in einem Kreis um P mit Radius a. Da A aber auf nur einer Seite von g liegt, liegt es auch in einem Halbkreis um P mit Radius a. Genauso liegt C in einem Halbkreis (auf der gleichen Seite von g wie der andere) um Q mit Radius c. Und genauso entsprechend liegt B in einer halben Ellipse mit den Brennpunkten P und Q und großer Halbachse b.

Abbildung: Zum Beweis, das Würmchen immer unter die Mini-Decke passt
65mm
\includegraphics[height=22mm]{loewu7_n}

Der ganze Wurm liegt also innerhalb einer Figur, die aus der Überlappung zweier Halbkreise und einer Halbellipse entsteht. Seien X und Y die Extremalpunkte dieser Figur auf g. Da die Halbellipse die Breite b hat und die Halbkreise die Radien a und c, ist der Abstand zwischen X und Y kleiner gleich a + b + c = 1. Nun ist die Halbellipse ,,flacher`` als ein Halbkreis der gleichen Breite, und alle Halbkreise haben einen Radius kleiner als 1/2, daher liegt die gesamte Figur in einem Halbkreis mit Durchmesser 1, was zu beweisen war.
Wer sich noch mehr für dieses Thema interessiert, kann in dem Buch ,,Spiel, Satz, Sieg für die Mathematik`` von Ian Stewart weiterlesen.


Fußnoten

... Formel1
Diese kann man natürlich noch ,,verbessern``, indem man zum Beispiel n = 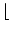$ \lfloor$log10N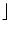$ \rfloor$ + 1 einsetzt. Sogar für V(N) kann man eine nur von N abhängige Formel finden, aber der Aufwand hiefür ist groß und bringt nicht viel.
drucken Zum Ausdrucken als pdf-File oder als ps-File