Beispiellösungen zu Aufgabenblatt 4

aktualisiert: 13. September 2002

Aufgabe 1

Für ein Verbrechen gibt es vier Verdächtige und jeder von ihnen macht eine Aussage:

Alfred: ,,Carlo ist es gewesen!``
Benno: ,,Ich war's nicht!``
Carlo: ,,Ede hat's getan!``
Ede: ,,Carlo hat gelogen, als er sagte, ich wäre es gewesen!``

Angenommen, nur genau einer der vier hat die Wahrheit gesagt. Wer hat dann das Verbrechen begangen? Und angenommen, nur einer der vier hat gelogen, wer war es dann?

Lösung:

1. Fall: Genau einer der vier hat die Wahrheit gesagt:

Wir gehen von den letzten beiden Aussagen aus. Carlo und Ede widersprechen sich, d. h. wenn Carlo die Wahrheit sagt, so lügt Ede und umgekehrt. Da es insgesamt nur eine wahre Aussage gibt, ist sie unter diesen beiden und Benno lügt. Also kann höchstens Benno der Täter sein.

Damit haben wir aber noch nicht alle Informationen ausgewertet und wissen somit noch nicht, ob das Problem überhaupt eine Lösung besitzt. Deshalb machen wir eine Probe: Wenn Benno der Täter ist, so lügen Alfred, Benno und Carlo. Ede sagt dann als einziger die Wahrheit.

2. Fall: Genau einer der vier hat gelogen:

Da Carlo und Ede sich widersprechen, sagt genau einer von ihnen die Wahrheit und der andere lügt. Da es insgesamt nur einen Lügner gibt, sagen die anderen beiden die Wahrheit. Also kann nur Carlo der Bösewicht sein.

Auch hier muss wieder eine Probe gemacht werden: Wenn Carlo der Bösewicht ist, so sagen Alfred, Benno und Ede die Wahrheit, Carlo jedoch lügt.

Aufgabe 2

Die Pfadfindergruppe Fähnlein Fieselschweif wandert in einer 1 km langen Schlange mit konstanter Geschwindigkeit durch das Göttinger Umland. Während die Schlange sich so weiterbewegt, läuft Fähnleinführer Tick (mit einer größeren konstanten Geschwindigkeit) einmal vom Ende der Schlange bis zur Spitze, um seine Mannen durchzuzählen, und wieder an seinen Platz am Ende der Gruppe zurück. Als er wieder hinten ankommt, ist die Schlange genau einen Kilometer weiter gewandert. Wie weit ist Tick gelaufen?

Lösung:

Bei solchen Aufgaben ist es nützlich, ein sogenanntes Weltliniendiagramm zu erstellen, ähnlich wie auf Blatt 1. Dies ist ein Koordinatensystem, auf dessen x-Achse die Zeit und auf dessen y-Achse der Ort aufgetragen wird. Der Schluss der Schlange befindet sich gemäß Aufgabenstellung zum Zeitpunkt Start am Ort 0 km, zum Zeitpunkt Ende am Ort 1 km, die entsprechenden Punkte A und B werden ins Diagramm eingezeichnet. Gleichförmige Bewegungen (d.h. solche mit konstanter Geschwindigkeit) entsprechen Geraden im Weltliniendiagramm. Verbindet man also die Punkte A und B im Diagramm, so kann man die Position des Schlusses der Schlange zu jedem Zeitpunkt zwischen Start und Ende ablesen.
Genauso zeichnet man die Punkte C und D ein, die die Position der Spitze der Schlange beschreiben. Nachdem man beide Punkte durch eine Gerade (gleichförmige Bewegung !) verbunden hat, hat das Weltliniendiagramm die Gestalt in Abbildung 1.

**Abbildung 1:** Weltliniendiagramm mit Spitze und Schluss der Schlange
$\includegraphics[]{tickv.eps}$

Jetzt muss noch die Weltlinie von Tick eingezeichnet werden. Diese wird durch drei Punkte bestimmt: den Punkten A und B, bei denen Tick zum selben Zeitpunkt am selben Ort ist wie der Schluss der Schlange, und einem Punkt U auf der Weltlinie der Spitze der Schlange, dessen Position zunächst unbestimmt ist. Die zu U gehörige Zeit wird mit Umkehr bezeichnet, der Ort mit x. Man erhält Abbildung 2.

**Abbildung 2:** Weltliniendiagramm mit Schlangenenden und Tick
$\includegraphics[]{tickd.eps}$

Wo genau liegt nun der Punkt U auf $\overline{{CD}}$ ? Nun, es gibt noch eine Bedingung: Tick läuft stets mit der (betragsmäßig) gleichen Geschwindigkeit, nur vor und nach der Umkehr in entgegengesetzte Richtungen. Der Anstieg von $\overline{{AU}}$ ist somit gleich dem negativen Anstieg von $\overline{{UB}}$ , als Gleichung:

$\displaystyle {\frac{{x}}{{t_{\text{Umkehr}} - t_{\text{Start}}}}}$ = - $\displaystyle {\frac{{-\left(x - 1\right)}}{{t_{\text{Ende}} - t_{\text{Umkehr}}}}}$ = $\displaystyle {\frac{{x - 1}}{{t_{\text{Ende}} - t_{\text{Umkehr}}}}}$

Ebenso erhält man aus der Weltlinie der Spitze der Schlange, deren Anstieg vor und nach dem Treffen gleich ist, eine Gleichung:

$\displaystyle {\frac{{x-1}}{{t_{\text{Umkehr}} - t_{\text{Start}}}}}$ = $\displaystyle {\frac{{2 - x}}{{t_{\text{Ende}} - t_{\text{Umkehr}}}}}$

Setzt man beide Gleichungen zusammen, so erhält man

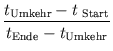$\displaystyle {\frac{{x}}{{x-1}}}$ = $\displaystyle {\frac{{t_{\text{Umkehr}} - t_{\text{ Start}}}}{{t_{\text{Ende}} - t_{\text{Umkehr}}}}}$ = $\displaystyle {\frac{{x-1}}{{2-x}}}$

Damit erhält man eine quadratische Gleichung für x:

x $\displaystyle \left(\vphantom{2-x}\right.$ 2 - x $\displaystyle \left.\vphantom{2-x}\right)$ = $\displaystyle \left(\vphantom{x-1)}\right.$ x - 1) $\displaystyle \left.\vphantom{x-1)}\right($ x - 1) $\displaystyle \Leftrightarrow$ 2x - x² = x² - 2x + 1 $\displaystyle \Leftrightarrow$ 0 = 2x² - 4x + 1

Diese Gleichung hat die zwei Lösungen

x_{1, 2} = 1± $\displaystyle \sqrt{{\frac 1 2}}$ ,

wie man dem Diagramm aber entnimmt, liegt x zwischen 1 und 2, also kommt nur die Lösung x₁ = 1 + ${\frac{1}{{\sqrt 2}}}$ in Betracht.
Jetzt ist es nicht mehr schwer, Ticks Weglänge s zu bestimmen. Denn es gilt

s = x + (x - 1) = 2x - 1 = 2 $\displaystyle \left(\vphantom{1+\frac 1{\sqrt 2}}\right.$ 1 + $\displaystyle {\frac{1}{{\sqrt 2}}}$ $\displaystyle \left.\vphantom{1+\frac 1{\sqrt 2}}\right)$ - 1 = 1 + $\displaystyle {\frac{{2}}{{ \sqrt{2}}}}$ = 1 + $\displaystyle \sqrt{2}$ $\displaystyle \approx$ 2, 41.

Tick legt also eine Wegstrecke von ca. 2,41 Kilometern zurück.

Aufgabe 3

Jemand zeichnet ein Dreieck ABC und auf jeder der Dreicksseiten noch einen Punkt P, Q bzw. R.

Als nun aber noch die drei Umkreise der drei Dreiecke ARQ, BPR und CQP eingezeichnet werden, stellt dieser jemand überrascht fest, dass sich diese Kreise in einem gemeinsamen Punkt M schneiden. Man wiederhole diese Prozedur an einem eigenen Beispiel noch einmal und versuche zu beweisen, dass sich die erwähnten Kreise immer in einem gemeinsamen Punkt schneiden müssen!

$\includegraphics[width=40mm]{aufg04_03.eps}$

Lösung:

Verwendet wird der (unter anderem vom letzten Musterlösungsblatt) bekannte Satz vom Sehnenviereck, nach dem die vier Ecken eines Vierecks genau dann auf einem Kreis liegen, wenn gegenüberliegende Innenwinkel zusammen 180^o ergeben.
Sei nun M der Schnittpunkt der Umkreise von Dreieck ARQ und Dreieck BPR. Wenn man zeigen kann, dass M auch auf dem dritten Umkreis liegt, ist die Aufgabe gelöst.

$\includegraphics[width=7cm]{loes04_03.eps}$

Abbildung 1

Es gilt aber nach dem eben erwähnten Sehnenvierecksatz:

$\displaystyle \alpha$ + $\displaystyle \alpha{^\prime}$ = 180^o (1)

und

$\displaystyle \beta$ + $\displaystyle \beta{^\prime}$ = 180^o (2)

Deswegen gilt auch:

$\displaystyle \gamma{^\prime}$ = 360^o - $\displaystyle \alpha{^\prime}$ - $\displaystyle \beta{^\prime}$ = 360^o - (180^o - $\displaystyle \alpha$ ) - (180^o - $\displaystyle \beta$ ) = $\displaystyle \alpha$ + $\displaystyle \beta$ (3)

Weil die Innenwinkelsumme im Dreieck ABC auch 180^o ist, folgt schließlich

$\displaystyle \gamma{^\prime}$ = 180^o - $\displaystyle \gamma$ (4)

Somit ist das Viereck MPCQ ein Sehnenviereck und der Umkreis von PCQ geht auch durch M.

Aufgabe 4

Ein Kohlenkeller hat die Form eines Quadrates der Seitenlänge 1. Drei Familien wollen diesen durch den Einbau von Trennwänden in drei flächengleiche Teile zerlegen. Eine Möglichkeit hierzu ist zum Beispiel die folgende:

$\includegraphics[width=35mm]{aufg04_04.eps}$

Die Gesamtlänge der eingebauten Wände ist hierbei 2. Trennwände sind nun aber ziemlich teuer und deswegen sollte man versuchen, die Gesamtlänge der Trennwände so kurz wie möglich zu wählen.
Man finde eine solche möglichst kurze Variante! (Die Trennwände müssen hierbei keineswegs immer gerade verlaufen!)

Lösung:

Bei dieser Experimentieraufgabe ging es wieder in erster Linie darum, dass man sich ein wenig mit dem Problem beschäftigt und vielleicht ein gewisses Gefühl dafür bekommt, worauf es bei der Aufgabe ankommt. -- Abbildung 4 zeigt die optimale Einteilung des Kellers:

**Abbildung 4:** Die optimale Einteilung
$\includegraphics[width=40mm]{kk3opt.eps}$

**Abbildung:** Die beste Einteilung mit nur geraden Wänden
$\includegraphics[width=40mm]{kk3idger.eps}$

Sie benötigt eine Wandlänge von ${\frac{{2}}{{3}}}$ + ${\frac{{\pi}}{{6}}}$ + ${\frac{{\sqrt{3}}}{{4}}}$ = 1,623278... (wenn die Seitenlänge des Quadrats gleich 1 ist). Wie kommt man auf so eine schöne, aber etwas willkürlich erscheinende Formel für die Länge? Sie ergibt sich aus den Konstruktionsmerkmalen der Figur: Sie ist symmetrisch (womit die mittlere Linie schon einmal ein Geradenstück ist), und die beiden seitlichen Linienzüge sind Kreisbögen, und zwar so, dass sie im rechten Winkel auf die Seitenwand stoßen und in der Mitte mit 120-Grad-Winkeln ankommen. Dabei ergibt sich nebenbei gesagt auch, dass der Radius der Kreisbögen genau 1 ist. Übrigens ist erwiesen, dass bei derlei Problemen nur Strecken und Kreisbögen zum Einsatz kommen und dass sie rechtwinklig auf Seitenwände stoßen müssen. Ein allgemeiner Beweis für das 120-Grad-Aufeinandertreffen von drei Linienzügen ist uns nicht bekannt, es erscheint aber aus verschiedenen Gründen recht logisch zu sein.

Will man nur gerade Mauern zulassen (etwa weil der Maurer keine Kurven mauern möchte), so ist die Einteilung in Abbildung 5 die beste; sie ist wiederum symmetrisch und hat eine Mauerlänge von ${\frac{{2}}{{3}}}$ + ${\frac{{\sqrt{15}}}{{4}}}$ = 1,634912...

Das herauszufinden erfordert einigen Aufwand. Vielleicht fällt einem eher die Einteilung in Abbildung 6 ein, die mit einer Wandlänge von 1 ${\frac{{2}}{{3}}}$ = 1,666... im Vergleich noch ganz gut da steht. Für's Auge hübsch, aber nicht ganz so sparsam sind auch noch die Einteilungen in Abbildung 7 mit Gesamtlängen von 1,75 bzw. 2.

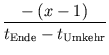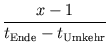
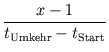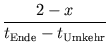
$\includegraphics[width=30mm]{kk3t.eps}$

Abbildung 2

**Abbildung:** Auch ganz hübsch
$\includegraphics[width=30mm]{kk3y.eps}$ $\includegraphics[width=30mm]{kk3a.eps}$

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File