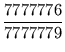Beispiellösungen zu Aufgabenblatt 5

aktualisiert: 1. November 2002

Aufgabe 1 Welche der beiden Zahlen ist die größere:

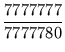$\displaystyle {\frac{{7777776}}{{7777779}}}$ oder $\displaystyle {\frac{{7777777}}{{7777780}}}$ ?

Hinweis: Die Benutzung von Taschenrechner bzw. Computer verstößt gegen die Mathematikerehre!

Lösung: Die zweite Zahl ist die größere.

Wie fast alle bemerkt hatten, kann man eine allgemeinere Aussage beweisen. Es gilt nämlich für alle natürlichen Zahlen n:

$\displaystyle {\frac{{n}}{{n+3}}}$ < $\displaystyle {\frac{{n+1}}{{n+4}}}$

Wie beweist man dies?
Dazu gehen wir von einer ,,offensichtlich`` wahren Aussage aus, die für alle natürlichen Zahlen n gilt:

n + 3 < n + 4

Multiplizieren wir beide Seiten mit -1, so kehrt sich das Relationszeichen um (da -1 < 0):

- (n + 3) > - (n + 4)

Jetzt dividieren wir beide Seiten durch n + 3, dabei bleibt das Relationszeichen erhalten, da n + 3 > 0 für alle natürlichen Zahlen n gilt:

-1 > - $\displaystyle {\frac{{n+4}}{{n+3}}}$

Jetzt teilen wir beide Seiten durch n + 4, dabei bleibt das Relationszeichen wieder erhalten, da auch n + 4 > 0:

- $\displaystyle {\frac{{1}}{{n+4}}}$ > - $\displaystyle {\frac{{1}}{{n+3}}}$

Wir multiplizieren beide Seiten mit 3:

- $\displaystyle {\frac{{3}}{{n+4}}}$ > - $\displaystyle {\frac{{3}}{{n+3}}}$

Nun muss man noch auf beiden Seiten 1 addieren, auch dies ändert an der Relation nichts:

1 - $\displaystyle {\frac{{3}}{{n+4}}}$ > 1 - $\displaystyle {\frac{{3}}{{n+3}}}$

Voilà! Sieht man genau hin, so erkennt man darin die gesuchte Ungleichung. Denn nach Erweitern gilt:

$\displaystyle {\frac{{n+4}}{{n+4}}}$ - $\displaystyle {\frac{{3}}{{n+4}}}$ > $\displaystyle {\frac{{n+3}}{{n+3}}}$ - $\displaystyle {\frac{{3}}{{n+3}}}$

und damit

$\displaystyle {\frac{{n+1}}{{n+4}}}$ > $\displaystyle {\frac{{n}}{{n+3}}}$

Jetzt setzt man noch n = 7777776 und hat das gesuchte Ergebnis.
Wer die allgemeinen Umformungen anzweifelt, der kann die Rechnung auch nachvollziehen, indem er überall n = 7777776 einsetzt, das reicht ja zur Lösung der Aufgabenstellung.

-.5cm 23.5cm

Aufgabe 2

Man finde die kleinste natürliche Zahl n mit folgender Eigenschaft:
Streicht man die letzte Ziffer von n und setzt sie vor die erste Ziffer, so entsteht eine Zahl, die genau viermal so groß ist wie n.

Lösung: Die natürliche Zahl n habe in Dezimalschreibweise die Ziffern a_k, a_k-1, $\hdots$ a₀ in dieser Reihenfolge (wobei a_k $\neq$ 0 sein soll), so dass also

n = a_k^.10^k + a_k-1^.10^k-1 + $\displaystyle \hdots$ a₁^.10 + a₀

gilt. Für die Zahl m, die aus n durch Streichen der letzten Ziffer a₀ und Voranstellen dieser Ziffer entsteht, gilt dann:

m = a₀^.10^k + a_k^.10^k-1 + $\displaystyle \hdots$ a₂^.10 + a₁

und die Bedingung der Aufgabe heißt dann m = 4^.n. Setzt man hier die Darstellungen für m und n ein, so folgt:

a₀^.10^k + a_k^.10^k-1 + $\displaystyle \hdots$ a₂^.10 + a₁ = 4^. $\displaystyle \left(\vphantom{a_k\cdot 10^k+a_{k-1}\cdot 10^{k-1}+\hdots a_1\cdot 10+a_0 }\right.$ a_k^.10^k + a_k-1^.10^k-1 + $\displaystyle \hdots$ a₁^.10 + a₀ $\displaystyle \left.\vphantom{a_k\cdot 10^k+a_{k-1}\cdot 10^{k-1}+\hdots a_1\cdot 10+a_0 }\right)$

oder umgeformt

$\displaystyle \left(\vphantom{10^k-4}\right.$ 10^k - 4 $\displaystyle \left.\vphantom{10^k-4}\right)$ ^.a₀ = 39^.a₁ + 390^.a₂ + $\displaystyle \hdots$ + $\displaystyle \left(\vphantom{39\cdot10^{k-1}}\right.$ 39^.10^k-1 $\displaystyle \left.\vphantom{39\cdot10^{k-1}}\right)$ ^.a_k

Auf der rechten Seite kann man 39 = 3^.13 ausklammern:

$\displaystyle \left(\vphantom{10^k-4}\right.$ 10^k - 4 $\displaystyle \left.\vphantom{10^k-4}\right)$ ^.a₀ = 3^.13^. $\displaystyle \left(\vphantom{ a_1+10\cdot a_2+\hdots+10^{k-1}\cdot a_k}\right.$ a₁ + 10^.a₂ + $\displaystyle \hdots$ + 10^{k-1 .}a_k $\displaystyle \left.\vphantom{ a_1+10\cdot a_2+\hdots+10^{k-1}\cdot a_k}\right)$

Da 13 eine Primzahl und a₀ eine Ziffer zwischen 0 und 9 ist, muss 13 also 10^k - 4 teilen. Geht man der Reihe nach die ersten Möglichkeiten für k durch, so findet man, dass 13 keine der Zahlen 6, 96, 996, 9996 teilt. Es gilt aber 13^.7692 = 99996 = 10⁵ - 4. Der kleinstmögliche Wert für k ist also 5. Setzt man dies in die letzte Gleichung ein, so folgt:

7692^.a₀ = 3^. $\displaystyle \left(\vphantom{ a_1+10\cdot a_2+\hdots+10^{4}\cdot a_5}\right.$ a₁ + 10^.a₂ + $\displaystyle \hdots$ + 10^{4 .}a₅ $\displaystyle \left.\vphantom{ a_1+10\cdot a_2+\hdots+10^{4}\cdot a_5}\right)$

oder, weil 3^.2564 = 7692 ist:

2564^.a₀ = a₁ + 10^.a₂ + $\displaystyle \hdots$ + 10^{4 .}a₅

Der kleinstmögliche Wert für a₀, für den 2564^.a₀ eine fünfstellige Zahl ist, ist a₀ = 4. Damit ist dann

a₁ + 10^.a₂ + $\displaystyle \hdots$ + 10^{4 .}a₅ = 4^.2564 = 10256

Deswegen ist der kleinstmögliche Wert, den ein n mit den geforderten Bedingungen annehmen kann, n = 102564.

Die (an dieser Stelle wichtige) Probe zeigt, dass diese Zahl wegen 4^.102564 = 410256 auch wirklich die gesuchte ist.

Ein kleiner Trick kann bei dieser Aufgabe hilfreich sein. Man denke sich nämlich die Zahl x als diejenige rationale Zahl, die die Ziffern unserer gesuchten Zahl n als Periode hat. Also

x = 0,a_ka_k-1 $\displaystyle \hdots$ a₁a₀a_ka_k-1 $\displaystyle \hdots$ a₁a₀ $\displaystyle \hdots$ = 0, $\displaystyle \overline{{a_ka_{k-1}\hdots a_1a_0}}$

Dann kann man zunächst

x + a₀ = a₀,a_ka_k-1 $\displaystyle \hdots$ a₁a₀a_ka_k-1 $\displaystyle \hdots$ a₁a₀ $\displaystyle \hdots$ = a₀, $\displaystyle \overline{{a_ka_{k-1}\hdots a_1a_0}}$

berechnen. Dividiert man diese Zahl durch 10, so verschiebt sich das Komma um eine Stelle, also:

y : = $\displaystyle {\frac{{1}}{{10}}}$ (x + a₀) = 0,a₀a_ka_k-1 $\displaystyle \hdots$ a₁a₀a_ka_k-1 $\displaystyle \hdots$ a₁a₀ $\displaystyle \hdots$ = 0, $\displaystyle \overline{{a_0a_ka_{k-1}\hdots a_1}}$

Diese Zahl y hat also die Ziffern der Zahl m = 4n als Periode, so dass nach Bedingung der Aufgabe y = 4^.x folgt. Setzt man die Gleichung für y hier ein, so findet man:

$\displaystyle {\frac{{1}}{{10}}}$ (x + a₀) = 4^.x

oder umgeformt nach x:

x = $\displaystyle {\frac{{a_0}}{{39}}}$

Da n nicht mit einer Ziffer 0 beginnen darf, muss die Periode von x auch mit einer von 0 verschiedenen Ziffer beginnen. Die kleinste Möglichkeit hierfür ergibt sich im Fall a₀ = 4, nämlich:

x = $\displaystyle {\frac{{4}}{{39}}}$ = 0, 102564102564102564 $\displaystyle \hdots$

Dies führt ebenfalls zur Lösung n = 102564.

Aufgabe 3

Eine Frauenstammtischrunde bestehend aus n Personen kommt jeden Freitag zusammen. Jede einzelne von ihnen spielt nun samstags Lotto und man kann natürlich nicht bis zum nächsten Freitag warten, um die Gewinnnachrichten der anderen zu erfahren. So vereinbart man, sich noch am selben Samstagabend über E-Mail auszutauschen, und zwar so, dass in jeder E-Mail die Absenderin alle Informationen weitergibt, die sie bisher erhalten hat. Eine Möglichkeit dazu wäre nun, dass jede jeder genau einmal eine E-Mail schreibt. Man will aber Telefonkosten sparen, also einigt man sich vorher, in welcher Reihenfolge wer wem eine E-Mail schreibt. Was ist die kleinstmögliche Anzahl von zu schreibenden E-Mails, bei der jede der Frauen vom Glück oder Pech jeder anderen erfährt?

Behauptung: Die kleinstmögliche Anzahl an E-Mails, bei der jede der Frauen alles erfährt, ist 2(n - 1).

Beweis: Eine mögliche Strategie (es gibt auch andere!):
Eine Frau wird zur Chefin gewählt. Am Samstagabend schicken alle anderen Frauen ihre Gewinnmeldung an die Chefin. Nach diesen n - 1 E-Mails weiß die Chefin alles. Sie schreibt alle Informationen in einer E-Mail zusammen, die sie nacheinander den anderen n - 1 Frauen schickt. Insgesamt sind dann 2(n - 1) E-Mails versendet worden.

Da dies aber nur einer von vielen denkbaren Wegen ist, bleibt die Frage: Kommt man auch mit weniger E-Mails aus?

Wir gehen davon aus, dass keine zwei E-Mails gleichzeitig abgesendet werden. Dann gibt es einen Zeitpunkt x, zu dem erstmalig eine Frau alle Informationen erhalten hat. Dazu muss aber jede der anderen ihre Meldung mindestens einmal verschickt haben, d.h. es sind mindestens schon n - 1 E-Mails verschickt worden. Da aber pro E-Mail jeweils nur eine Frau etwas dazuerfahren kann, muss nach dem Zeitpunkt x jede der anderen n - 1 Frauen noch mindestens eine weitere E-Mail erhalten.

Also müssen insgesamt mindestens 2(n - 1) E-Mails verschickt werden.

Aufgabe 4

Auf kariertem Papier ist folgende Figur aufgemalt:

Wenn man sich einmal die Mühe macht, die Kästchen in der Figur auszuzählen, so stellt man fest, dass es genau 64 sind. Das sind bekanntlich 8^.8, also sollte es doch möglich sein, die Figur entlang der Kästchenkanten so in genau zwei Teile zu zerteilen, dass man aus ihnen ein Quadrat der Seitenlänge 8 zusammenlegen kann, oder?

$\includegraphics[width=50mm]{aufg05_04.eps}$

Lösung: jaja Allen anders lautenden Behauptungen zum Trotz: Es gibt eine Lösung. Zum Beweis geben wir ganz einfach den entsprechenden Schnitt an. Der rechte Teil ist um den eingezeichneten Punkt um 90 Grad im Uhrzeigersinn zu drehen, dann passt er genau an den linken und es entsteht ein Quadrat.

$\includegraphics[width=50mm]{loes05_04a.eps}$ $\includegraphics[width=50mm]{loes05_04b.eps}$

Warum stellen wir eine solche Aufgabe in unserem Mathezirkel? Weil man die Aufgabe nicht nur durch Probieren, sondern auch durch logisches Denken lösen und dabei gleichzeitig beweisen kann, dass es nur diese eine Lösung gibt. (Als Mathematiker möchte man ja immer alles sehr genau wissen...)
Um es ganz formal zu beginnen: Wir nehmen einmal an, dass es eine Lösung gibt. (Diese formelle Annahme hat einen Vorteil: Sollten wir jetzt nach einigen logischen Folgerungen zu einem Widerspruch kommen, so muss unsere Annahme falsch sein. Und das bedeutet dann, dass wir bewiesen haben, dass es keine Lösung gibt.)

Zunächst schauen wir uns die rechte Spitze der Figur an, in der linken Zeichnung unten mit Ziffer 1 markiert. Sie gehört zu dem einen Teil (er heiße A), den wir durch einen Schnitt aus der Figur erhalten. Da in einem 8×8-Quadrat keine zwei kleinen Quadrate mehr als sieben Schritte in eine Richtung voneinander entfernt sind, gehören alle mit einer 2 bezeichneten Quadrate zu dem anderen Teil, B. Schaut man sich nun z. B. die linke untere Ecke an, so merkt man entsprechend, dass alle mit 3 bezeichneten Felder zu A gehören.

$\includegraphics[width=50mm]{loes05_04c.eps}$ $\includegraphics[width=50mm]{loes05_04d.eps}$

Da Teil B nun schon acht Felder hoch ist, kann Teil A nur rechts oder links daran angelegt werden. Auf der linken Seite geht das aber nicht, da A dann rechteckig sein müsste. Jetzt kann man sich überlegen, wie A wohl gedreht werden kann, damit es an die rechte Seite von B passt. Wir lassen B so liegen, wie es ist. A muss die rechte obere Ecke des Quadrats stellen, weil dort noch nichts ist, deswegen kann es weder nur verschoben werden noch um 90 Grad gegen den Uhrzeigersinn gedreht werden, weil dann die kleine 2×1-,,Spitze``über den Rand herausragt.

Soll A um 180 Grad gedreht werden, muss das Feld mit der Nummer 4 die rechte obere Ecke werden, weil einerseits B mindestens drei Felder breit ist und A daher maximal fünf Felder breit sein darf, andererseits ja A im dann oberen Teil mindestens vier Kästchen breit sein muss. Da die Felder 5 und 6 von A überdeckt würden, dürfen sie nicht zu B gehören, machen andererseits damit A zu breit - Widerspruch!

Also wird A um 90 Grad um Uhrzeigersinn gedreht. Jetzt nehmen wir schließlich an, Feld 5 gehöre zu B. Dann kann A in der nach der Drehung rechten Spalte nicht mehr volle acht Kästchen hoch sein; da es aber die rechte obere Ecke belegen muss, muss Feld 7 zu B gehören. Felder 6 und 8 auch, weil sonst A über den oberen Rand hinausragen würde. Felder 9 können nicht mehr zu A gehören, weil sie nur noch an Felder grenzen, die bereits zu B gehören. Damit kann A aber nicht mehr die fünf Kästchen breit sein, die es schon sicher breit ist (Felder 3) - Widerspruch!

Damit muss Feld 5 zu A gehören, das dann die rechte obere Ecke bilden wird. Nun werden langsam die Bezeichnungen unübersichtlich, daher gilt jetzt die rechte Figur. Weil A die 3×4 - Lücke oben füllen muss, gehören die Felder 6 und a zu A. Die Felder b können von A nicht bedeckt werden, sie gehören zu B. Weil 5 und 6 in B ,,fehlen``, müssen Felder c auch zu A gehören. Schließlich bleiben noch die Felder d bei B und e bei A.

Damit haben wir aus der Annahme, es gebe (irgendeine) Einteilung, genau die oben angegebene Schnittweise hergeleitet, somit also bewiesen, dass es genau diese eine Lösung gibt.

Völlig richtig wurde von einer Teilnehmerin angemerkt, dass es nicht bei jeder Figur mit 64 Kästchen möglich ist, sie mit einem Schnitt in zwei Teile zu zerlegen, die zusammengelegt ein Quadrat ergeben. Das dürfte sogar nur in den wenigsten Fällen machbar sein. Wir haben die Aufgabe in diesem Punkt etwas ,,vorlaut`` formuliert.

Allen anders lautenden Behauptungen zum Trotz: Es gibt eine Lösung. Allerdings auch nur genau eine, die man mit etwas systematischem Probieren finden kann.
Da es langweilig wäre, wenn wir die Lösung einfach verraten würden, empfehlen wir, ruhig noch ein bisschen weiter zu probieren. Es ist kein Trick dabei. Wichtig ist, dass man die Figur geeignet in genau zwei Teile zerlegt. Dann dreht man eines der Teile und setzt die beiden Teile zum gesuchten Quadrat zusammen.
Wer es trotzdem nicht erwarten kann, der sollte mal auf unsere Homepage (siehe Fußnote) schauen, dort findet man bald die Lösung.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File