Beispiellösungen zu Aufgabenblatt 7

aktualisiert: 26. Januar 2001

Aufgabe 1

Die handelsüblichen Papierformate DIN A0, DIN A1 usw. haben folgende praktische Eigenschaften:

Die Seitenverhältnisse verschiedener Formate sind immer dieselben. Das heißt, wenn zum Beispiel a₃ und b₃ (mit a₃ > b₃) die Seitenlängen eines DIN-A3-Blattes sind und a₅ und b₅ (mit a₅ > b₅) die Seitenlängen eines DIN-A5-Blattes, so verhält sich a₃ zu b₃ wie a₅ zu b₅.
Halbiert man ein Blatt vom Format DIN A(k), so erhält man zwei Blätter vom Format DIN A(k + 1) (das k ist hierbei ein Platzhalter für die Zahlen 0, 1, 2, 3 usw.).
Ein Blatt vom Format DIN A0 hat eine Fläche von genau einem Quadratmeter.

Bestimme aus diesen Angaben das Seitenverhältnis im DIN-Format, die Seitenlängen eines DIN-A0-Blattes und die Seitenlängen eines DIN-A4-Blattes. Überprüfe das letzte Ergebnis durch direktes Nachmessen!

Lösung:

Wie in der Aufgabe seien a_n und b_n (mit a_n > b_n) die Seitenlängen des DIN-A(n)-Blattes (ohne Angabe der Einheiten).

Die erste Bedingung sagt, dass für alle n

$\displaystyle {\frac{a_{n}}{b_{n}}}$ = $\displaystyle {\frac{a_{n+1}}{b_{n+1}}}$

(1)

gilt. Die zweite Bedingung lautet

a_{n + 1} = b_n und b_{n + 1} = $\displaystyle {\textstyle\frac{1}{2}}$ a_n .

(2)

Setzt man (2) in (1) ein, so erhält man

$\displaystyle {\frac{a_n}{b_n}}$ = $\displaystyle {\frac{a_{n+1}}{b_{n+1}}}$ $\displaystyle \;\stackrel{(2)}{=}\;$ $\displaystyle {\frac{b_n}{\frac{1}{2}a_n}}$ = 2 $\displaystyle {\frac{b_n}{a_n}}$ .

Multiplizieren mit a_n und mit b_n liefert

a_n² = 2b_n² .

Da alle Zahlen positiv sind, liefert Wurzelziehen

a_n = $\displaystyle \sqrt{2}$ b_n .

Damit ergibt sich für die Seitenverhältnisse

$\displaystyle {\frac{a_n}{b_n}}$ = $\displaystyle \sqrt{2}$ .

Mit der dritten Bedingung

a₀b₀ = 1

(3)

kann man noch die Seitenlängen ausrechnen:

1 ^. $\displaystyle \sqrt{2}$ = a₀b₀ $\displaystyle \sqrt{2}$ = a₀ $\displaystyle {\frac{1}{\sqrt{2}}}$ a₀ $\displaystyle \sqrt{2}$ = a₀² ,

also

a₀ = $\displaystyle \sqrt[4]{2}$ und b₀ = $\displaystyle {\frac{1}{a_0}}$ = $\displaystyle {\frac{1}{\sqrt[4]{2}}}$ .

Die Seiten des DIN-A0-Blattes sind also $\sqrt[4]{2}$ m $\approx$ 1,1892 m und ${\frac{1}{\sqrt[4]{2}}}$ m $\approx$ 0,8409 m lang.

Es gilt außerdem

a₄ $% latex2html id marker 765 $\displaystyle \;\stackrel{(\ref{2})}{=}\;$$ b₃ $% latex2html id marker 766 $\displaystyle \;\stackrel{(\ref{2})}{=}\;$$ $\displaystyle {\textstyle\frac{1}{2}}$ a₂ $% latex2html id marker 768 $\displaystyle \;\stackrel{(\ref{2})}{=}\;$$ $\displaystyle {\textstyle\frac{1}{2}}$ b₁ $% latex2html id marker 770 $\displaystyle \;\stackrel{(\ref{2})}{=}\;$$ $\displaystyle {\textstyle\frac{1}{4}}$ a₀ = $\displaystyle {\textstyle\frac{1}{4}}$ $\displaystyle \sqrt[4]{2}$

und zusammen mit den ausgerechneten Seitenverhältnissen auch

b₄ = $\displaystyle {\frac{1}{\sqrt{2}}}$ a₄ = $\displaystyle {\textstyle\frac{1}{4}}$ $\displaystyle {\frac{1}{\sqrt{2}}}$ a₀ = $\displaystyle {\textstyle\frac{1}{4}}$ b₀ = $\displaystyle {\textstyle\frac{1}{4}}$ $\displaystyle {\frac{1}{\sqrt[4]{2}}}$ .

Damit sind die Seiten des DIN-A4-Blattes ${\frac{1}{4}}$ $\sqrt[4]{2}$ m $\approx$ 29,73 cm und ${\frac{1}{4}}$ ${\frac{1}{\sqrt[4]{2}}}$ m $\approx$ 21,02 cm lang.

Aufgabe 2

Zwei Bauarbeiter schaufeln Sand. Schaufelt jeder von ihnen nacheinander die Hälfte des Sandes, so benötigen sie dafür insgesamt 25 Stunden. Wenn sie aber gleichzeitig schaufeln, so schaffen sie diese Arbeit in nur 12 Stunden.
Wie lange würde jeder der beiden allein für den gesamten Haufen benötigen?

Lösung:

Es seien a₁ und a₂ Zahlen, die die Arbeitsleistungen der Bauarbeiter widerspiegeln, und zwar in der Weise, dass a_i ^.t angibt, welchen Anteil des Sandberges Arbeiter Nr. i in der Zeit t wegschaufelt. Wenn t₁ und t₂ die Zeit darstellen, die die Arbeiter jeweils brauchen, um den Sandberg alleine wegzuschaufeln, gilt also

t₁a₁ = 1 und t₂a₂ = 1 .

(4)

Nach der zweiten Voraussetzung der Aufgabenstellung gilt, weil beide zusammen den gesamten Haufen in genau 12 Stunden abtragen:

12 ^.(a₁ + a₂) = 1 .

(5)

Die erste Voraussetzung besagt dann:

$\displaystyle {\frac{t_1}{2}}$ + $\displaystyle {\frac{t_2}{2}}$ = 25 .

(6)

Unter Verwendung von (4) kann man (5) schreiben als

12 ^. $\displaystyle \left(\vphantom{ \frac{1}{t_1} + \frac{1}{t_2} }\right.$ $\displaystyle {\frac{1}{t_1}}$ + $\displaystyle {\frac{1}{t_2}}$ $\displaystyle \left.\vphantom{ \frac{1}{t_1} + \frac{1}{t_2} }\right)$ = 1

und mit weiteren Umformungen erhält man: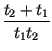

1 = 12 ^. $\displaystyle \left(\vphantom{ \frac{1}{t_1} + \frac{1}{t_2} }\right.$ $\displaystyle {\frac{1}{t_1}}$ + $\displaystyle {\frac{1}{t_2}}$ $\displaystyle \left.\vphantom{ \frac{1}{t_1} + \frac{1}{t_2} }\right)$ = 12 ^. $\displaystyle {\frac{t_2+t_1}{t_1t_2}}$ $% latex2html id marker 812 $\displaystyle \;\stackrel{(\ref{s3})}{=}\;$$ $\displaystyle {\frac{600}{t_1 t_2}}$ , .

also

t₁t₂ = 600 .

Das liefert zusammen mit (6) ( t₂ = 50 - t₁):

t₁² - 50t₁ + 600 = 0 .

Bisher war in keiner Weise unterschieden, welcher Arbeiter wie schnell schaufelte. Daher müssen die beiden Lösungen der quadratischen Gleichung -- t₁ = 25± $\sqrt{25^2-600}$ = 25±5 -- auch schon die beiden gesuchten t_i's sein; bestimmt man Arbeiter Nr. 1 zum schnelleren, bekommt man demnach:

t₁ = 20 sowie t₂ = 30 .

Sie brauchen also 20 bzw. 30 Stunden, wenn sie den Sand alleine wegschaufeln.

Aufgabe 3

Auf einem Zahlenstrahl sitzt ein n-Frosch (das ist ein Frosch mit einer besonderen Vorliebe für die Zahl n).
Er bewegt sich auf dem Zahlenstrahl nach folgender Regel:
Sitzt ein n-Frosch auf der Zahl m und ist m > n, so macht der n-Frosch einen n-Sprung nach links und landet auf der Zahl m - n. Ist aber m < n, so ändert der Frosch seine Vorliebe, wird zum m-Frosch und springt zum Abschied auf die Zahl n. Ist schließlich irgendwann m = n, so ist der n-Frosch glücklich und bleibt sitzen.

Beschreibe den Weg eines 21-Frosches, der zu Beginn auf der Zahl 12 sitzt, und den eines 35-Frosches, der auf der 11 startet!
Versuche noch weitere Beispiele und stelle eine Vermutung auf, wo ein a-Frosch landet, wenn er auf b startet! Beweise diese Vermutung!
Wo also landet ein 1000000-Frosch, wenn er zu Beginn auf 123456789 steht?

Lösung:

Zunächst einmal kann man, wie in der Aufgabe gefordert, feststellen, dass ein auf 12 beginnender 21-Frosch letztlich auf der 3 landet und der 35-Frosch, der auf 11 beginnt, am Ende auf der 1 sitzt.
Nach einer Reihe weiterer Beispiele stellt man schließlich fest, dass der Frosch jedes Mal nach einiger Hüpferei auf einer Zahl sitzen bleibt. Das ist von vornherein keineswegs offensichtlich, schließlich macht der Frosch gelegentlich auch auf dem Zahlenstrahl ziemlich weite Sprünge in Richtung größerer Zahlen. Man muss also erst einmal beweisen, dass der Frosch in jedem Fall irgendwann zur Ruhe kommt. Dies könnte man wie folgt tun:
Man gibt einem m-Frosch auf dem Feld n einen gedanklichen Wert m + n und überlegt sich, wie sich dieser Wert des Frosches bei seinem Gehüpfe ändert. Im Fall m < n springt der Frosch nach links und landet auf n - m, dann ist sein Wert auf m + (n - m) = n geschrumpft. Ist jedoch m > n, so springt der Frosch nach rechts zum Feld m, wird dafür aber zum n-Frosch; sein Wert bleibt also gleich m + n. Im nächsten Schritt allerdings springt er dann als n-Frosch nach m - n und sein Wert wird kleiner. Man sieht also: Bei fortwährender Springerei wird der Wert des Frosches wenigstens jeden zweiten Schritt kleiner. Da der Frosch am Anfang nur einen endlichen Wert hat, und der Wert (offensichtlich) nicht negativ werden kann, muss der Frosch nach einiger Zeit aufhören zu springen -- was er genau dann tut, wenn m = n ist.
Aber wo hört er auf?
Hier hilft nur, durch viele Beispiele Ideen zu sammeln. Mit der richtigen Idee ist es dann nicht schwer, Folgendes zu beweisen:
Steht ein m-Frosch vor Beginn eines Schrittes auf n und ist nach diesem Schritt zum m'-Frosch geworden (das kann sich ja geändert haben) und steht auf n', so gilt in jedem Fall ggT(n, .m) = ggT(n', .m').
Hierbei steht ggT(a, .b) für den größten gemeinsamen Teiler der Zahlen a und b.
Der Beweis hierzu ist nicht schwer. Ist m > n, so tauschen m und n nur die Rollen und es ist klar, dass ggT(m, .n) = ggT(n, .m) = ggT(m', .n') gilt. Ist m = n, so bleibt der Frosch sitzen, und dann ändert sich auch am ggT nichts. Der einzig interessante Fall ist m < n. Dann ist zu zeigen, dass ggT(m,n) = ggT(m,n - m) gilt. Das gilt aber, denn ist t ein Teiler von m und n, so ist n = n₁ ^.t, m = m₁ ^.t, also n - m = (n₁ - m₁) ^.t. Damit ist t auch ein Teiler von n - m. Ist umgekehrt t Teiler von n - m und m, also n - m = u ^.t und m = v ^.t, so ist n = (n - m) + m = (u + v) ^.t, folglich teilt t auch n. Man sieht daher, dass die gemeinsamen Teiler von n und m genau die gemeinsamen Teiler von m und n - m sind. Also ist auch der größte gemeinsame Teiler derselbe.
Hört der Frosch nun irgendwann als m-Frosch auf einem Feld n auf zu springen (und das tut er, wie oben bewiesen!), so ist n = m. Ist der Frosch ursprünglich als a-Frosch bei b gestartet, so ist dann ggT(a,b) = ggT(m,n) = ggT(n,n) = n.
Der Frosch landet also in jedem Fall auf dem Feld ggT(a,b).
Da 1000000 nur die Primfaktoren 2 und 5 hat, die 123456789 sicherlich nicht hat, landet der 1000000-Frosch, der bei 123456789 startet, letztendlich bei ggT(1000000,123456789) = 1.

PS: Vielleicht kennt der eine oder die andere den Euklidischen Algorithmus zur Bestimmung des größten gemeinsamen Teilers zweier natürlicher Zahlen -- der Frosch führt im Prinzip genau diesen Algorithmus aus!

Aufgabe 4

Lege auf einen Tisch von den Spielkartenfarben Karo, Herz, Pik und Kreuz jeweils den Buben, die Dame, den König und das Ass.
Ist es möglich, diese Karten quadratisch so anzuordnen, dass in jeder Reihe und in jeder Spalte jede Farbe und jedes Bild genau einmal vorkommt?

Lösung:

Das Problem wurde schon im 18. Jh. von Leonhard Euler unter dem Namen der orthogonalen Lateinischen Quadrate untersucht. Ihm zu Ehren wird heute eine Lösung auch als Eulersches Quadrat bezeichnet.
Eine Möglichkeit, die 16 Karten anzuordnen, ist in der Abbildung dargestellt. Man kann leicht überprüfen, dass in keiner Zeile oder Spalte eine Farbe oder ein Bild doppelt vorkommt und dass jede Karte genau einmal verwendet wurde.

Zwar gibt es viele andere mögliche Lösungen, aber sie lassen sich alle auf diese eine zurückführen. Zum einen ist es nämlich so, dass eine Lösung schon eindeutig durch fünf geeignet gewählte Karten festgelegt ist. (Das ist nicht offensichtlich und der Beweis ist auch recht lang, deshalb verzichten wir hier darauf.) Aber daran liegt es, dass man beim Suchen einer Lösung leicht auf Schwierigkeiten stößt, denn wenn man dann bei der sechsten Karte nicht zufällig die richtige legt, kann man keine Anordnung mehr finden und stößt früher oder später auf einen Widerspruch.
Andererseits erhält man aus einer beliebigen Lösung wieder eine Lösung, wenn man Zeilen, Spalten oder auch Farben oder Bilder untereinander vertauscht. Durch diese ,,Umformungen`` kann man aus einer beliebigen Lösung eine Lösung erzeugen, die mit der Abbildung in den fünf oben gewählten Karten übereinstimmt.(Auch dies soll hier nicht bewiesen werden.) Und dann stimmt sie auch mit der gesamten Abbildung überein, denn es gibt ja wie oben gesagt nur eine Lösung mit diesen fünf Karten an diesen Stellen.

Die Aufgabe kann verallgemeinert werden, indem man n² Karten mit n verschiedenen Werten aus einem Spiel mit n verschiedenen Farben nimmt. Damit hat sich L. Euler beschäftigt und 1779 vermutet, dass es für n = 6 keine Lösung gibt. Das wurde 1900 bewiesen. Eulers Vermutung, dass es für alle durch 2, aber nicht durch 4 teilbaren Zahlen keine Lösung gibt, war allerdings ziemlich falsch: Seit Mitte des 20. Jh. weiß man, dass es außer für n = 2 und n = 6 für alle natürlichen Zahlen n eine Lösung gibt.

Wenn ihr Lust habt, könnt ihr mal ein Computerprogramm schreiben, das dieses Problem untersucht und zu gegebener Kartenanzahl eine oder alle Lösungen ermittelt.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File