Beispiellösungen zu Aufgabenblatt 22

aktualisiert: 13. November 2002

Aufgabe 1


Leonard zeichnet mehrere gerade Linien auf ein Blatt Papier, jeweils von einer Kante des Blattes zu einer anderen. Bei näherem Hinschauen sieht er, dass er die Linien so gezeichnet hat, dass jede Linie jede andere schneidet und keine drei Linien sich in einem Punkt schneiden. Er zählt nun nach, dass auf diese Weise das Blatt in 22 Teile aufgeteilt wurde.

a)
Wie viele Linien hat Leonard gezeichnet?

b)
Erhält man immer 22 Teile, wenn man genauso viele Linien wie Leonard zeichnet, die sich auf dieselbe Weise schneiden?

c)
(Zusatzfrage) Wie lautet die Antwort bei mehr oder weniger Linien? Versuche eine Formel anzugeben, um die Anzahl der Teile zu berechnen.


Lösung:


Wir beantworten zuerst die Zusatzfrage c), wonach sich die anderen Antworten leicht geben lassen.
Gehen wir davon aus, Leonard habe schon n - 1 Linien ( n $ \in$ $ \mathbb {N}$) wie in der Aufgabe angegeben gezeichnet. Nun wird gezählt, wie viele Flächenstücke hinzukommen, wenn Leonard die n-te Linie zeichnet. Angefangen beim Blattrand beginnt er, die erste Fläche in zwei Teile zu zerlegen. Sobald er auf eine andere Linie trifft, hat er die erste Fläche zerlegt und beginnt eine neue zu zerlegen. Nach Voraussetzung trifft er auf n - 1 Linien, und zwar jede an einer anderen Stelle, d. h. er hat insgesamt n - 1 + 1 = n Flächenstücke zerlegt.
Wenn Leonard also die n-te Linie gezeichnet hat, hat sich die Zahl der Flächenstücke um n erhöht.
Wir können also eine rekursive Formel für die Anzahl A(n) der Flächenstücke bei n Linien angeben:

A(n) = A(n - 1) + n

Außerdem gilt:    A(0) = 1     (wenn keine Linie eingezeichnet ist, haben wir eine große Fläche.)
Daraus erhält man:
A(n) = A(n - 1) + n = A(n - 2) + (n - 1) + n = ...  
  = A(0) + 1 + 2 + ... + (n - 1) + n  
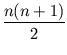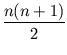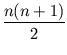    und mit der Summenformel: 1 + ... + n = $\displaystyle {\frac{{n(n+1)}}{{2}}}$  
A(n) = A(0) + $\displaystyle {\frac{{n(n+1)}}{{2}}}$ = 1 + $\displaystyle {\frac{{n(n+1)}}{{2}}}$  

Da an keiner Stelle die genaue Lage der Linien benutzt wurde, hängt die Anzahl der Flächenstücke nur von der Anzahl der Linien ab, weshalb die Frage b) mit ,,Ja`` zu beantworten ist.
Probiert man für n die Zahlen 1, 2, 3,... durch, so erhält man schließlich wegen 1 + $ {\frac{{6 \cdot 7}}{{2}}}$ = 22, dass Leonard 6 Linien gezeichnet hat.


Aufgabe 2


Für Lenas Glückszahl x gilt

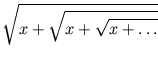
3 = $\displaystyle \sqrt{{x+\sqrt{x+\sqrt{x+\dots}}}}$

Welche Zahl bringt Lena Glück?


Lösung:


Lenas Glückszahl hat eine schöne Eigenschaft. Es gilt

3 = 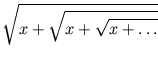$\displaystyle \sqrt{{x+\sqrt{x+\sqrt{x+\dots}}}}$  
9 = x + 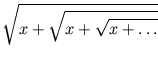$\displaystyle \sqrt{{x+\sqrt{x+\sqrt{x+\dots}}}}$  
  = x + 3.  

Also ist x = 9 - 3 = 6.

Bemerkung: Wenn es nicht vorausgesetzt wäre, dass mindestens eine Zahl existiert, die die Gleichung erfüllt, so müsste diese Existenz noch gezeigt werden.


Aufgabe 3


Bauer Hauser hat 4 Söhne, unter denen er sein großes Feld, das die Form eines konvexen Vierecks hat, aufteilen möchte. Hierzu verwendet er folgende Methode (Bezeichnungen wie in der Skizze): Er misst die Mitten Ma bis Md der Seiten und die Mitte M der Diagonale $ \overline{{BD}}$ ab. Der erste Sohn bekommt dann das Viereck AMaMMd, der zweite das Viereck BMbMMa, der dritte CMcMMb und der vierte DMdMMc.

\includegraphics[width=5cm]{feld.eps}

Ist diese Aufteilung gerecht, bzw. unter welchen Umständen wird welcher Sohn bevorteilt?


Lösung:


Je nach Gestalt des Feldes wird entweder der erste oder der dritte Sohn bevorteilt und der andere benachteiligt. Der zweite und der vierte Sohn bekommen auf jeden Fall je ein Viertel der Gesamtfläche.

Betrachten wir getrennt die Dreiecke ABD und BCD.
Im Dreieck ABD sind Ma und M nach Aufgabenstellung die Seitenmitten der Seiten $ \overline{{AB}}$ bzw. $ \overline{{BD}}$, d. h. bei zentrischer Streckung um B mit Faktor $ {\frac{{1}}{{2}}}$ geht das Dreieck ABD in das Dreieck MaBM über. Die Fläche des Dreiecks MaBM ist also gerade $ \left(\vphantom{\frac{1}{2}}\right.$$ {\frac{{1}}{{2}}}$$ \left.\vphantom{\frac{1}{2}}\right)^{2}_{}$ = $ {\frac{{1}}{{4}}}$ -mal so groß wie die Fläche des Dreiecks ABD. Entsprechend geht bei zentrischer Streckung um D mit Faktor $ {\frac{{1}}{{2}}}$ das Dreieck ABD in das Dreieck MdMD über, weshalb auch dessen Fläche gerade $ {\frac{{1}}{{4}}}$ -mal so groß ist wie die des Dreiecks ABD.
Die gleiche Überlegung im Dreieck BCD liefert, dass die Flächen der Dreiecke BMbM und MMcD gerade $ {\frac{{1}}{{4}}}$-mal so groß ist wie die des Dreiecks BCD.
Daraus erhält man nun folgende Flächengrößen: Der erste Sohn bekommt die Hälfte der Fläche des Dreiecks ABD (zwei Viertel der Dreiecksfläche fehlen) und der dritte Sohn bekommt die Hälfte der Fläche des Dreiecks BCD. Für die anderen beiden Söhne bleibt je ein Viertel des Dreiecks ABD und ein Viertel des Dreiecks BCD, also gerade ein Viertel der gesamten Fläche.
Somit wird der erste Sohn bevorteilt, wenn das Dreieck ABD eine größere Fläche hat als das Dreieck BCD, und der dritte Sohn wird bevorteilt, wenn die Fläche des Dreiecks ABD kleiner ist. Nur wenn beide Flächen gleich sind, ist die Aufteilung gerecht.

Bemerkung: Ist P der Schnittpunkt der Diagonalen $ \overline{{AC}}$ und $ \overline{{BD}}$ des Vierecks ABCD, so treten die verschiedenen Fälle ein, wenn | AP| > | PC| bzw. | AP| < | PC| bzw. | AP| = | PC| gilt.


Aufgabe 4


Monika rechnet etwas mit Zahlen herum. Sie geht dabei folgendermaßen vor:
Sie beginnt mit vier natürlichen Zahlen (alle größer als 0). Sie bildet alle möglichen Paare dieser Zahlen (erste und zweite Zahl, erste und dritte Zahl, ..., vorletzte und letzte Zahl). Falls die Zahlen eines Paares verschieden sind, subtrahiert sie die kleinere von der größeren. Alle erhaltenen Differenzen schreibt sie auf ein neues Blatt Papier.

Mit den Zahlen dieses neuen Blattes geht sie nun genauso vor: Paare bilden, Differenzen ausrechnen, Differenzen auf ein neues Blatt schreiben.

Dies macht sie so lange, bis auf einem Blatt entweder nur noch genau eine Zahl oder gar keine Zahl mehr steht.

a)
Zeige, dass Monika nur endlich viele Blatt Papier verwenden muss.

b)
Gibt es Anfangszahlen, bei denen am Schluss eine Zahl übrig bleibt, oder endet Monikas Prozedur immer mit einem leeren Blatt?


Beispiel für Monikas Rechnung:
Sie beginnt mit den Zahlen 2, 5, 5 und 8 und erhält als Differenzen: 5 - 2 = 3, 5 - 2 = 3, 8 - 2 = 6 , 8 - 5 = 3 und 8 - 5 = 3 ( 5 und 5 sind nicht verschieden; das Paar (5, 5) wird also nicht weiter betrachtet). Auf dem neuen Blatt Papier stehen also die Zahlen 3, 3, 3, 3 und 6.
Nach erneuter Ausführung der Prozedur stehen auf dem dritten Blatt die Zahlen 3, 3, 3 und 3.
In allen sechs Paaren (jeweils bestehend aus 3 und 3) dieser Zahlen sind die beiden Zahlen gleich. Somit bleibt das nächste Blatt leer und Monika kann nicht mehr weiterrechnen.


Lösung:


a)
Auf Monikas erstem Blatt (dies sei das mit den Anfangszahlen) gibt es eine größte Zahl, n (evtl. in mehrfacher Ausführung). Alle Differenzen, die mit ihr gebildet werden, werden mit natürlichen Zahlen gebildet, die größer als null sind. Daher sind diese Differenzen und damit offensichtlich auch alle anderen gebildeten Differenzen kleiner oder gleich n - 1. Dieselbe Argumentation gilt natürlich weiter für alle anderen Blätter, womit folgt, dass auf dem k-ten Blatt alle Zahlen kleiner oder gleich n - (k - 1) sind. Da keine Zahlen kleiner gleich 0 vorkommen können, ist spätestens mit dem (n + 1)-ten Blatt Schluss.

b)
Nein, es kann nicht vorkommen, dass Monika am Ende genau eine Zahl auf einem Blatt stehen hat. Zum Beweis sei angenommen, dies sei doch der Fall. Dann müssen auf dem vorletzten Blatt genau zwei, und zwar voneinander verschiedene Zahlen gestanden haben. 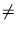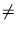(Denn wenn die Zahlen alle gleich gewesen wären, wäre keine Differenz ungleich null gewesen, so dass nichts notiert worden wäre; wären es mehr als zwei Zahlen gewesen, die nicht alle gleich sind, so wären darin also mindestens drei Zahlen a, b, c mit a $ \neq$ b $ \neq$ c (evtl. a = c) enthalten. Diese hätten jedoch mindestens die beiden Zahlen | a - b| und | b - c| für den letzten Zettel geliefert.)

Um zwei verschiedene Zahlen zu erhalten, müssen auf dem drittletzten Zettel mindestens drei verschiedene Zahlenwerte gestanden haben, a > b > c Diese bilden jedoch drei von null verschiedene Differenzen, a - b, a - c und b - c, was zum Widerspruch führt. Daher ist die Annahme zu Beginn falsch, der genannte Fall kann also nicht vorkommen.


Für die richtige Lösung ist wichtig, dass gleiche Differenzen, wenn sie mehrfach auftreten, auch wie angegeben mehrfach notiert werden. Andernfalls wird immer das Ende mit einer verbleibenden Zahl eintreten, wie man sich klarmachen kann.

drucken Zum Ausdrucken als pdf-File oder als ps-File