Wir betrachten zwei verschiedene Punktmengen in der (x, y)-Ebene: Zum einen
die Menge aller Punkte, die die Gleichung
x2 + y2 = 1 erfüllen, zum
anderen diejenigen Punkte, die die Gleichung
y = x2 + t mit einem frei
bestimmbaren Parameter t erfüllen.
Für welche Werte von t haben die beiden Mengen genau einen Punkt gemeinsam?
Rechnerische Lösung:
Da die x-Koordinate der Punkte in beiden Gleichungen nur zum Quadrat
vorkommt, gilt für jeden Punkt (x, y), der im Schnitt der beiden Mengen
liegt, dass auch der Punkt (- x, y) im Schnitt liegt. Sollen also beide Mengen
genau einen Punkt gemeinsam haben, so muss für diesen Punkt x = 0 gelten.
Damit gilt für die y-Koordinate: y2 = 1 und y = t.
Somit gilt: t2 = 1, d. h. t = 1 oder t = - 1.
Die einzigen möglichen Werte von t sind also 1 und -1.
Berechnen wir für diese beiden Werte alle Punkte, die die zwei Mengen
gemeinsam haben.
Fall t = 1: Aus x2 + y2 = 1 und y = x2 + 1 folgt y - 1 + y2 = 1.
| y2 + y - 2 = 0 | |||
y1, 2 = - 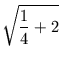 |
|||
| y1 = 1 und y2 = - 2 |
Für y1 = 1 erhält man durch Einsetzen in die erste Gleichung wie gewünscht x = 0 und eine Probe zeigt, dass der Punkt (0, 1) wirklich beide Gleichungen erfüllt. Für y2 = - 2 erhält man x2 = - 3, d. h. keine Lösung.
Somit ist t = 1 ein gesuchter Wert.
Fall t = - 1: Aus x2 + y2 = 1 und y = x2 - 1 folgt y + 1 + y2 = 1.
| y2 + y = 0 | |||
| y(y + 1) = 0 | |||
| y1 = 0 und y2 = - 1 |
Für y1 = 0 erhält man nun x2 = 1, d. h. x = 1 oder x = - 1. Eine Probe zeigt, dass die beiden Punkte (- 1, 0) und (1, 0) tatsächlich beide Bedingungen erfüllen. Somit liegen schon zwei Punkte im Schnitt der beiden Mengen und t = - 1 ist somit keiner der gesuchten Werte.
Also ist t = 1 der einzige Wert, bei dem die beiden Mengen genau einen Punkt gemeinsam haben.
Geometrische Lösung:
Die Gleichung x2 + y2 = 1 beschreibt einen Kreis mit Radius 1 um den Ursprung (0, 0) der Ebene; y = x2 + t ist eine um t auf der y-Achse verschobene (nach oben geöffnete) Normalparabel. Auch hier sieht man sofort, dass beide Figuren symmetrisch zur y-Achse sind (d. h. im Vergleich zu ersten Lösung: mit (x, y) ist auch (- x, y) Schnittpunkt). Ein einfacher Schnittpunkt kann also nur auf der y-Achse (s. o. x = 0) liegen und muss somit der Scheitelpunkt (0, t) der Parabel sein. Auch hier bleiben nur die beiden Schnittpunkte des Kreises mit der y-Achse, nämlich (0, 1) und (0, - 1), zu betrachten.
Für t = 1 ist sofort ersichtlich, dass es keinen weiteren Schnittpunkt geben kann, denn die anderen Punkte der Parabel liegen alle oberhalb dieses Schnittpunktes, die des Kreises unterhalb.
Für t = - 1 müssen wir ein wenig mehr überlegen. Anschaulich sieht man, dass der Kreis in seinem ,,Südpol`` flacher als die Parabel ist, so dass die Parabel sich zunächst im Inneren des Kreises bewegt und es noch einen weiteren Schnittpunkt geben muss.
Mathematisch korrekter ist aber sicherlich, weitere Schnittpunkte (die sich von einer Zeichnung gut erraten lassen), nämlich (- 1, 0) und (1, 0), anzugeben.
![\includegraphics[width=10cm]{kreisparabel.eps}](img4.png)
Also ist t = 1 der einzige Wert, bei dem die beiden Mengen genau einen Punkt gemeinsam haben.
Aufgabe 2
Prinz Siegfried soll zwei Drachen töten, um die schöne Prinzessin zu
bekommen.
Beide Drachen haben 1000 Köpfe. Siegfried kann ihnen mit einem Hieb seines
Schwertes Excalibur wahlweise genau
13, 17, 20 oder 5 Köpfe abschlagen,
woraufhin aber sofort 22, 2, 14 bzw. 17 Köpfe nachwachsen (bei 13
abgeschlagenen wachsen also 22 nach, bei 17 abgeschlagenen wachsen 2 nach
usw.).
Es ist überliefert, dass der eine Drache genau dann stirbt, wenn er (nach
dem Nachwachsen) genau 333 Köpfe hat; der andere stirbt, wenn ihm alle
Köpfe abgeschlagen wurden (in diesem Fall wächst keiner mehr nach).
Welche(n) der Drachen kann Siegfried jemals töten, und wenn ja, wie, bzw. wenn nein, warum nicht?
Lösung:
Siegfried wird die Prinzessin nicht bekommen, denn er kann nur den zweiten
Drachen töten. Beim ersten müht er sich vergeblich.
Um dies einzusehen, überlegt man sich zunächst, wie sich die Anzahl der
Köpfe nach einem Schlag und dem anschließenden Nachwachsen ändert. Da bei
13 abgeschlagenen Köpfen 22 nachwachsen, ändert sich die Kopfzahl
hierbei insgesamt um +9, genauso sieht man, dass ein Abschlagen von 17, 20
bzw. 5 Köpfen zu einer Nettoänderung der Kopfzahl von -15, -6 und
+12 führt.
Die wichtige Beobachtung ist nun, dass all diese Nettoänderungen durch 3
teilbar sind. Die Gesamtzahl der Köpfe ändert sich also stets um Vielfache
von 3 und daher bleibt der Rest, den die Kopfzahl bei Division durch 3
lässt, unverändert. Zu Beginn hat der Drachen 1000 Köpfe, was bei
Division durch 3 den Rest 1 lässt. Also können nie 333 Köpfe
erreicht werden, weil 333 durch 3 teilbar ist, also den Rest 0 lässt.
Der zweite Drachen hat nicht soviel Glück. Ihm kann Siegfried zunächst
47-mal 20 Köpfe abschlagen, worauf jeweils wieder 14 nachwachsen. Die
Gesamtzahl an Köpfen beträgt danach
1000 - 47 . 20 + 47 . 14 = 718. Danach
kann er ihm wieder 47-mal 17 Köpfe abschlagen, jedesmal wachsen dem
Drachen dann sofort 2 Köpfe nach und es verbleiben ihm
718 - 47 . 17 + 47 . 2 = 13 Köpfe. Die letzten 13 Köpfe entfernt Siegfried dann mit
einem Hieb.
Zur vollständigen Lösung muss noch geprüft
werden, ob Siegfried jeden Hieb auch ausführen kann (bei einer rechnerischen
Lösung, die nur mit den Netto-Änderungen arbeitet, kann es passieren, dass
Siegfried z. B. 20 Köpfe abschlagen soll, obwohl nur noch 19 vorhanden
sind). Dies macht hier jedoch keine Probleme: Im ersten Durchgang werden
47 . 20 = 940, also insgesamt weniger als 1000 Köpfe abgeschlagen. Vor dem
vorletzten Hieb muss der Drache noch
13 + (17 - 2) = 28 Köpfe haben. Somit
hat Siegfried noch reichliche Auswahlmöglichkeiten, 17 Köpfe zu entfernen,
erst recht bei den anderen 17er-Hieben zuvor.
Aufgabe 3
Yvonne wirft sechsmal eine 1-Euro-Münze und Zacharias wirft dieselbe
Münze siebenmal.
Wie groß ist die Wahrscheinlichkeit dafür, dass Zacharias öfter ,,
Zahl`` wirft als Yvonne?
Lösung:
Der einfachste Ansatz wäre sicherlich, die
Möglichkeiten zu zählen, die zum Gewinn von Zacharias führen, und
durch die Anzahl aller Wurfmöglichkeiten zu teilen. Je nach Methode kann dies
aber schnell unübersichtlich werden. Eleganter finden wir die folgende
Argumentation:
Um die gesuchte Wahrscheinlichkeit zu berechnen, betrachten wir zusätzlich auch den Fall, dass Zacharias öfter als Yvonne ,,Adler`` wirft.
Da Zahl und Adler gleich häufig sind, ist die Wahrscheinlichkeit, dass Zacharias öfter als Yvonne Zahl wirft, genauso groß wie die Wahrscheinlichkeit, dass er öfter als Yvonne Adler wirft.
Wie wir gleich zeigen werden, sind diese beiden Ereignisse komplementär
zueinander (d. h. der eine Fall tritt genau dann ein, wenn es der andere nicht
tut). Damit ist die Wahrscheinlichkeit jeweils
![]() .
.
Da Zacharias öfter als Yvonne die Münze wirft, muss er eine der beiden
Münzseiten (Zahl oder Adler) auch öfter erhalten. Da er aber nur einmal mehr
wirft, kann nur eine der beiden Seiten bei ihm öfter als bei Yvonne vorkommen.
Es tritt also tatsächlich genau einer der beiden Fälle (entweder
Zahl oder Adler öfter) ein.
Aufgabe 4
Eine Einbahnstraße wird von einer nicht abbrechenden Folge von Autos
befahren. Die Autos haben jeweils die Breite 2 m und die Länge 5 m und fahren
im Normalverkehr mit der Geschwindigkeit 10 m/s und mit einem Abstand von
jeweils 10 m zueinander, im Berufsverkehr nur mit der
Geschwindigkeit 1, 5 m/s und mit einem Abstand von 5 m zueinander am
rechten Straßenrand.
Peter überquert die Straße senkrecht mit der Geschwindigkeit 2 m/s, ohne auf
den Verkehr zu achten.
- Wie groß ist in beiden Fällen die Wahrscheinlichkeit dafür, daß Peter die Straße unverletzt überquert?
- Kann Peter diese Wahrscheinlichkeit vergrößern (und wenn ja, um wie viel), indem er in anderer als senkrechter Richtung (aber weiterhin geradlinig) die Straße überquert?
(Was hier beschrieben wird, ist natürlich ganz und gar nicht im Sinne eines vernünftigen Verhaltens im Verkehr. Daher bitte ,,rein mathematisch`` betrachten und nicht selbst ausprobieren!)
Lösung:
- Peter braucht genau eine Sekunde, um den 2 m breiten Gefahrenbereich mit
seiner Geschwindigkeit von 2 m/s zu durchqueren. Die effektive Breite der
Lücke zwischen den Autos, d. h. die Breite des Bereiches, in dem er bei
Eintritt in den Fahrbahnbereich die Straße heil überquert, berechnet sich aus
der tatsächlichen Breite (10 m bzw. 5 m) minus der Strecke, die die Autos in
einer Sekunde zurücklegen. Denn Peter muss zum einen natürlich die Straße
betreten, wenn gerade kein Auto vor seiner Nase ist, und er muss nach links
noch so viel Platz haben, wie ein Auto in der Zeit zurücklegt, die er zum
Überqueren braucht, sonst wird ihn das nächste Auto erfassen.
Die Wahrscheinlichkeit ergibt sich dann aus dem Quotienten der effektiven Breite, sofern diese größer gleich null ist, und der Länge eines ,,repräsentativen Bereichs``, d. h. der Länge von einem Auto plus einer Lücke. Ist die effektive Breite kleiner als null, ist die Wahrscheinlichkeit offensichtlich null.
Das ergibt für den Normalverkehr eine Wahrscheinlichkeit von
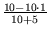 = 0 und für den Berufsverkehr von
= 0 und für den Berufsverkehr von
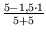 = 0, 35.
= 0, 35.
- Wir können den Fall ignorieren, dass Peter den Autos entgegenläuft -
seine Chancen würden nur schlechter werden. Wir betrachten seine
Geschwindigkeit in die beiden Komponenten vs senkrecht zur und vp
parallel zur Fahrtrichtung aufgeteilt.
![\includegraphics[width=6cm]{vgeteilt.eps}](img8.png)
Es gilt vs2 + vp2 = v2 = 4. Peter braucht jetzt t =
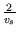 Sekunden, um die Straße zu überqueren. Da er aber ein wenig nach rechts geht,
hat die effektive Breite der Lücke den Wert
Sekunden, um die Straße zu überqueren. Da er aber ein wenig nach rechts geht,
hat die effektive Breite der Lücke den Wert
lLücke - t . vAuto + t . vp = lLücke - 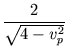 . vAuto +
. vAuto + 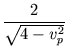 . vp,
. vp,
sofern dies nicht größer als die Breite der Lücke lLücke wird - das hieße nämlich, dass Peter dann von hinten in ein Auto hineinrennt.Für den Normalverkehr ergibt sich als optimaler Wert (aus der Bestimmung der Nullstelle der Ableitung) vp = 0, 4 (mit
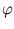
 11, 5o) und
damit eine Wahrscheinlichkeit von
11, 5o) und
damit eine Wahrscheinlichkeit von
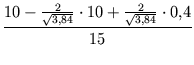
 0, 0135.
0, 0135.
Im Berufsverkehr geht Peter sogar schneller als die Autos. Damit kann er vp = vAuto erreichen (mit
 48, 6o), so dass er die
volle Lücke zwischen den Autos ausnutzen kann. Hier ist die Wahrscheinlichkeit
also
48, 6o), so dass er die
volle Lücke zwischen den Autos ausnutzen kann. Hier ist die Wahrscheinlichkeit
also
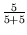 =
= 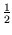 .
.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
