Beispiellösungen zu Aufgabenblatt 30

aktualisiert: 2. November 2003

Aufgabe 1


Auf einem quadratischen Schachbrett mit 121 Feldern steht auf jedem Feld eine Spielfigur. Nachdem jemand das Brett versehentlich umgestoßen hat, stellt er die Figuren erneut auf. Kann es passieren, dass dabei jede Figur auf ein Feld gestellt wird, das zu dem Feld, auf dem sie vorher stand, benachbart ist?


Lösung:


Nein, das kann nicht passieren.
Färbt man die Felder des Brettes wie üblich abwechselnd schwarz und weiß, wobei man mit schwarz in einer Ecke beginnt, so sieht man, dass es insgesamt 61 schwarze und 60 weiße Felder gibt. Die Nachbarfelder von schwarzen Feldern sind dabei stets weiße Felder und umgekehrt. Die 61 Spielfiguren, die zu Beginn auf den schwarzen Feldern stehen, können demnach nach dem erneuten Aufstellen nicht alle auf (weißen) Nachbarfeldern landen.


Aufgabe 2


Nina denkt sich drei aufeinander folgende Zahlen, deren Summe ungerade ist, und bildet deren Produkt. Michael, der weder die drei Zahlen noch deren Produkt kennt, möchte möglichst viele Teiler des Produktes erraten.
Welche Teiler kann Michael auf jeden Fall nennen?


Lösung:


Nina kann sich zum Beispiel die drei Zahlen 2, 3, 4 denken. Deren Produkt ist 24 und deswegen kann Michael in keinem Fall andere Teiler als die Teiler von 24, nämlich 1, 2, 3, 4, 6, 8, 12, 24, nennen.

Andererseits müssen, damit die Summe der drei von Nina gedachten Zahlen ungerade ist, genau zwei der drei Zahlen gerade sind. Dies sind dann die erste und die letzte Zahl. Von zwei aufeinander folgenden geraden Zahlen ist aber eine sogar durch 4 teilbar. Damit ist das Produkt in jedem Fall durch 8 teilbar. Da unter drei aufeinander folgenden Zahlen auch stets eine durch 3 teilbar ist (und 3 und 8 teilerfremd sind), muss das Produkt der von Nina gedachten Zahlen stets durch 24 teilbar sein. Michael kann also in der Tat in jedem Fall die Teiler 1, 2, 3, 4, 6, 8, 12, 24 nennen (und wie oben gesehen auch keine anderen).


Aufgabe 3


Sechs Studenten gehen in die Mensa. Jedes der drei angebotenen Essen haben sie genau zweimal geholt. Wie viele Möglichkeiten gibt es, die sechs Studenten so an einen runden Tisch mit sechs Stühlen zu setzen, dass diejenigen mit gleichem Essen nicht nebeneinander sitzen? Anordnungen, die sich nur durch eine Drehung unterscheiden, sollen als gleich gelten.


Lösung:


Eine Person sitze auf einem fest gewählten Platz. Ihr ,,Partner`` (mit gleichem Essen) kann ihr nun gegenübersitzen (1. Fall; eine Möglichkeit) oder aber mit genau einem Platz Abstand (2. Fall; zwei Möglichkeiten [rechts oder links]) von ihr Platz nehmen.

Im ersten Fall kann man auf einen festen der übrigen Plätze einen der vier übrigen Studenten setzen. Dessen Partner hat dann noch zwei Möglichkeiten und die übrigen beiden Studenten können sich dann noch auf zwei verschiedene Arten setzen. Das ergibt 4 . 2 . 2 = 16 Varianten.

Im zweiten Fall hat man für den Platz zwischen den beiden zuerst betrachteten Studenten noch vier Möglichkeiten, ihn zu besetzen, gegenüber diesem Platz muss dann aber der Partner dazu sitzen, damit die restlichen beiden nicht nebeneinander sitzen. Diese können aber noch untereinander tauschen, was noch einen Faktor 2 ergibt. Das sind hier also nur 4 . 2 = 8 Möglichkeiten. Dies müssen wir aber mal 2 nehmen, da es zwei Möglichkeiten für den 2. Fall gab, so dass wir insgesamt auf 16 + 2 . 8 = 32 Möglichkeiten kommen.


Anmerkung: Es war offenbar nicht ganz klar, dass wir jeweils zwischen den beiden Studenten mit gleichem Essen unterscheiden wollten. Tut man dies nicht (betrachtet man also nur die Anordnungen der Essen), so erhält man im ersten Fall (die beiden Leute eines fest gewählten Essens sitzen sich gegenüber) drei Möglichkeiten (zwei dafür, dass sich die anderen auch gegenüber sitzen, bei einer sitzen sie sich nicht gegenüber) und im zweiten Fall noch zwei Möglichkeiten (zwischen links und rechts wird nicht mehr unterschieden, aber man kann wählen, welches der Essen sich gegenüber sitzen soll), insgesamt also fünf Möglichkeiten.


Aufgabe 4


Lisa hat fleißig quadratische Tischdeckchen mit 40 cm Seitenlänge für ihren Kaffeetisch gehäkelt. Leider ist ihr Tisch nur 79,5×79,5 cm2 groß. Wie viele ihrer neuen Deckchen bekommt sie auf ihren Tisch, ohne dass diese aufeinander liegen oder über die Tischkante ragen?


Lösung:


Wir betrachten zunächst nur ein einziges auf dem Tisch liegendes Deckchen und zeigen folgende Hilfsaussage:

Behauptung: Wenn eines der beschriebenen Häkeldeckchen auf dem Tisch liegt, dann wird der Mittelpunkt des Tisches von dem Deckchen bedeckt, und zwar liegt er nicht nur auf dem Rand des Deckchens (d. h.: der Mittelpunkt liegt im Inneren des Quadrates, das das Deckchen darstellt).

Zum Beweis nehmen wir das Gegenteil an: dass wir ein Deckchen so hingelegt haben, dass der Tischmittelpunkt M nicht in dessen Innerem liegt.

Verlängert man die vier Kanten der Deckchenquadrats zu Geraden, so muss es mindestens eine geben, bezüglich der M auf der anderen Seite als das Deckchenquadrat liegt - oder im Grenzfall auf ihr liegt. Wir drehen den Tisch so, dass ABCD links unterhalb dieser Geraden liegt (bzw. bei seitenparalleler Auflage des Deckchens unterhalb davon) und führen Bezeichnungen ein, die sich aus der folgenden Skizze ergeben:

\includegraphics[height=6.8cm]{loes30_4_1.eps}
Was wäre, wenn ...


Nach Wahl der Lagebeziehungen können wir die Decke noch so weit wie möglich nach links und nach unten verschieben, ohne dass M unter die Decke gerät. Wir können also annehmen, dass D auf PQ und C auf PS liegt.

Zur Vereinfachung der Notation werde die Seitenlänge der Decke mit l = 40cm bezeichnet.

Nun werden Koordinaten eingeführt: P liege im Ursprung, D auf (a, 0) und C auf (0, b). Dann hat A die Koordinaten (a + b, a) und B die Koordinaten (b, a + b). Dabei gilt nach der Dreiecksungleichung: a + b $ \geq$ l > 0 und außerdem a2 + b2 = l2. Die Geradengleichung der Geraden (AB) lautet y = (x - b) . (- b)/a + (a + b).

\includegraphics[height=7.35cm]{loes30_4_2.eps}

Der Schnittpunkt dieser Geraden mit der Diagonalen x = y berechnet sich aus:

  x = (x - b) . (- b)/a + a + b
$\displaystyle \Leftrightarrow$ ax = - b(x - b) + a2 + ab
$\displaystyle \Leftrightarrow$ (a + b)x = a2 + ab + b2 = 1/2 . (a2 + 2ab + b2   +  a2 + b2)
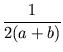$\displaystyle \Leftrightarrow$ x = $\displaystyle {\frac{{1}}{{2(a+b)}}}$((a + b)2 - 2(a + b)l + l2   +  2(a + b)l )
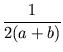    = $\displaystyle {\frac{{1}}{{2(a+b)}}}$(a + b - l )2 + l
    $\displaystyle \geq$ l.

Der Schnittpunkt S hat also Koordinaten (s, s) mit s $ \geq$ l. M hat die Koordinaten (l - 0, 25cm, l - 0, 25cm). Das heißt, dass S gleichzeitig weiter von P entfernt sein soll als M und auf der Geraden (AB) liegen soll, bezüglich der P und M nicht auf derselben Seite liegen (allenfalls liegt M auf (AB), dann müssten M und S zusammenfallen) - ein Widerspruch. Damit ist unsere Annahme falsch und die Behauptung bewiesen.


Nun ist der Rest einfach: Jede ordnungsgemäß platzierte Tischdecke muss also den Mittelpunkt des Tisches echt überdecken. Damit würde aber eine zweite Decke eine erste überdecken, was nicht sein soll, und somit kann Lisa immer nur eine Decke auflegen.

drucken Zum Ausdrucken als pdf-File oder als ps-File