Zu Ehren des 39. Aufgabenblattes betrachten wir alle Vielfachen der Zahl 39.
Was ist die Menge aller Quersummen dieser Zahlen?
Lösung:
Als Quersummen kommen genau die Vielfachen von 3 vor:
3, 6, 9, 12,...
(Um Missverständnissen vorzubeugen: In dieser Aufgabe verstehen wir unter den
natürlichen Zahlen
![]() N die positiven ganzen Zahlen ohne Null, und ebenso
betrachten wir die Zahl Null nicht als Vielfaches einer natürlichen Zahl.)
N die positiven ganzen Zahlen ohne Null, und ebenso
betrachten wir die Zahl Null nicht als Vielfaches einer natürlichen Zahl.)
Da
39 = 3 . 13 ist, sind alle Vielfachen von 39 auch Vielfache von
3, ihre Quersumme ist also jeweils durch 3 teilbar.
Umgekehrt kommen auch alle Vielfachen von 3 als Quersumme eines Vielfachen von 39 vor:
Es ist 10101 = 39 . 259 ein Vielfaches von 39, das die Quersumme 3 hat. Mit seiner Hilfe können wir nun systematisch alle Vielfachen von 3 als Quersumme eines Vielfachen von 39 erzeugen. Indem wir die 10101 zweimal hintereinander schreiben, erhalten wir eine Zahl 1010110101 mit Quersumme 6, die ebenfalls ein Vielfaches von 39 ist:
| 1010110101 | = 1010100000 + 10101 = 10101 . 105 + 10101 | |
| = 39 . 259 . 105 + 39 . 259 = 39 . (259 . 105 + 259). |
Genauso hat 101011010110101 die Quersumme 9 und ist Vielfaches von 39:
| 101011010110101 | = 10101 . 105 . 2 + 10101 . 105 + 10101 | |
| = 39 . (259 . 105 . 2 + 259 . 105 + 259). |
Setzen wir das so fort, erhalten wir, dass k . 3 Quersumme der Zahl
| 10101 . 105 . (k-1) + 10101 . 105 . (k-2) +...+ 10101 . 105 . 1 + 10101 | |||
| = 39 . (259 . 105 . (k-1) + 259 . 105 . (k-2) +...+ 259 . 105 . 1 + 259) |
ist, also ebenfalls Quersumme eines Vielfachen von 39.
Ein paar Anmerkungen zur Aufgabe (und zur Zahl 39):
Vielfache von 39 mit Quersummen 6 und 9 - und damit nach dem oben beschriebenen Prinzip des Voreinandersetzens auch mit allen größeren durch 3 teilbaren Zahlen - finden sich mit 312 und 117 recht schnell, die 10101 als kleinstes Vielfaches mit Quersumme 3 zugegebenermaßen nicht.
Wie findet man so ein Vielfaches mit kleiner Quersumme im Allgemeinen? Ganz kurz gesagt: Man muss die Reste betrachten, die die Potenzen von 10 beim Teilen durch die zu untersuchende Zahl lassen, und dann schauen, ob man es schafft oder nicht, wenige dieser Reste zu einer durch die Zahl teilbaren Summe zu addieren. (Das Addieren der Reste entspricht dem Erhöhen der entsprechenden Ziffern!)
Und wie sieht die (Gesamt-)Lösung dieser Aufgabe im Allgemeinen aus? Das ist
schwierig. Klar ist sofort: Für eine durch 9 teilbare
Zahl kommen nur Zahlen aus
9![]() N in Frage (also Vielfache von 9), für eine
durch 3, aber nicht durch 9 teilbare Zahl nur Zahlen aus
3
N in Frage (also Vielfache von 9), für eine
durch 3, aber nicht durch 9 teilbare Zahl nur Zahlen aus
3![]() N. Für alle
anderen Zahlen hat man, wenn man nur Teilbarkeit durch 3 betrachtet, keine
Einschränkung.
N. Für alle
anderen Zahlen hat man, wenn man nur Teilbarkeit durch 3 betrachtet, keine
Einschränkung.
Jedoch ergibt sich schnell eine andere Einschränkung, indem man sich Folgendes
überlegt: Eine Quersumme 1 kann nur eine Zahl der Form 10k haben. Und diese
Zahlen können nur Vielfache von Zahlen sein, die von der Form 2i5j mit
i, j ![]()
![]() N0 sind. Weitere Einschränkungen zu finden ist schon schwieriger und
geht mehr oder weniger in die Tiefen der Zahlentheorie.
N0 sind. Weitere Einschränkungen zu finden ist schon schwieriger und
geht mehr oder weniger in die Tiefen der Zahlentheorie.
Es gibt anscheinend (so genau wissen wir das im Allgemeinen auch nicht) viele
Zahlen, bei denen in der Tat die Menge der Quersummen
ihrer Vielfachen eine der sich aus dem oben Gesagten ergebenden Mengen
![]() N,
N,
![]() N
N ![]() {1},
3
{1},
3![]() N oder
9
N oder
9![]() N ist.
Jedoch gibt es auch viele, die nicht alle diese Zahlen als
Quersummen ihrer Vielfachen zulassen, z. B. die 11: Sie hat nur Vielfache mit
Quersummen aus der Menge
{2, 4, 6, 8, 10, 11, 12, 13,...}. Oder die 33:
Bei ihr ist es die Menge
{6, 12, 15, 18, 21,...}. Schließlich hat
41 die 5 als kleinste Quersumme eines Vielfachen, danach kommt erst die 10 und
dann alle weiteren natürlichen Zahlen. (Zum Teil ist dies sogar nicht allzu
schwer einzusehen - sei dies eine Aufforderung, sich damit auseinanderzusetzen
...)
N ist.
Jedoch gibt es auch viele, die nicht alle diese Zahlen als
Quersummen ihrer Vielfachen zulassen, z. B. die 11: Sie hat nur Vielfache mit
Quersummen aus der Menge
{2, 4, 6, 8, 10, 11, 12, 13,...}. Oder die 33:
Bei ihr ist es die Menge
{6, 12, 15, 18, 21,...}. Schließlich hat
41 die 5 als kleinste Quersumme eines Vielfachen, danach kommt erst die 10 und
dann alle weiteren natürlichen Zahlen. (Zum Teil ist dies sogar nicht allzu
schwer einzusehen - sei dies eine Aufforderung, sich damit auseinanderzusetzen
...)
Es gibt sogar Zahlen, bei denen eine beliebig vorgegebene Anzahl von den ersten natürlichen Zahlen in dieser Liste fehlt! Andererseits ist für jede Zahl in der Liste der Quersummen der Vielfachen ab irgendeinem Wert jeder größere Wert vorhanden, bzw. je nach Teilbarkeit durch 3 jeder größere durch 3 bzw. 9 teilbare Wert.
Im ,,Lexikon der Zahlen``1 steht unter dem Stichwort 39: ,,Anscheinend die erste uninteressante Zahl (was diese Zahl natürlich besonders interessant macht, weil sie die erste Zahl mit dieser Eigenschaft ist).`` Da nun die Menge der Quersummen gleich der nach recht einfachen Überlegungen maximal möglichen Menge ist, ist die 39 auch unter diesem Gesichtspunkt nicht sonderlich interessant; allenfalls ist bemerkenswert, dass man für keine andere durch 3 und nicht durch 9 teilbare Zahl kleiner 57 so weit suchen muss, um ein Vielfaches mit Quersumme 3 zu finden. Das aber rechtfertigt sicherlich nicht einen Eintrag in besagtem Buch. Tut uns Leid für die 39; immerhin hat sie jetzt hier Beachtung gefunden.
Aufgabe 2
Katrin und Wolfgang spielen folgendes Spiel: Sie markieren auf einem Blatt
Papier die Ecken eines regelmäßigen 2004-Ecks. Nun dürfen sie
abwechselnd ziehen, wobei ein Zug darin besteht, zwei Ecken, die bisher noch
nicht benutzt worden sind, durch eine Strecke zu verbinden. Dabei darf diese
Strecke allerdings keine der bisher schon gezeichneten Strecken schneiden.
Verloren hat, wer keinen erlaubten Zug mehr machen kann. Wenn Katrin den ersten
Zug macht, wer kann dann den Gewinn erzwingen?
Lösung:
Katrin kann den Sieg erzwingen.
Als Erstes verbindet sie zwei diametral gegenüberliegende Ecken, d. h. wenn wir die Ecken reihum von 1 bis 2004 durchnummerieren, so verbindet sie die Ecken 1 und 1003. Damit hat sie die Figur in zwei gleich geformte 1003-Ecke zerlegt, die wie Spiegelbilder zueinander sind. Alle weiteren Strecken müssen entweder in der einen oder in der anderen Hälfte gezogen werden, denn keine neue Strecke darf die erste schneiden.
Wenn Wolfgang dann einen Zug macht (er ist nach Katrins erstem Zug dran), kann Katrin denselben Zug in der anderen Hälfte ausführen, nur spiegelbildlich. Da danach die beiden Teile wieder Spiegelbilder voneinander sind (mitsamt allen eingezeichneten Strecken), kann Katrin auch weiterhin Spiegelbilder von Wolfgangs Zügen malen. Irgendwann kann dann Wolfgang keinen Zug mehr machen und hat verloren.
Aufgabe 3
Auf einem Holzbrett sind n Nägel eingeschlagen (n ![]() 2). Jemand möchte
ein geschlossenes Gummiband so entlang der Nägel spannen, dass jeder Nagel
vom Gummiband berührt wird und sich das Band nirgends selbst überkreuzt.
2). Jemand möchte
ein geschlossenes Gummiband so entlang der Nägel spannen, dass jeder Nagel
vom Gummiband berührt wird und sich das Band nirgends selbst überkreuzt.
Ist dies stets möglich oder gibt es ungünstige Verteilungen der Nägel,
bei denen das nicht der Fall ist?
Lösung:
Es ist immer möglich, ein Gummiband so zu spannen, dass es alle Nägel berührt.
![\includegraphics[height=35mm]{nagel1.eps}](img5.png)
![\includegraphics[height=35mm]{nagel2.eps}](img6.png)
![\includegraphics[height=35mm]{nagel3.eps}](img7.png)
Zum Beweis dieser Aussage geben wir zunächst ein Verfahren an, welches in
jedem Fall eine gesuchte Umspannung erzeugt
und zeigen anschließend, dass dieses Verfahren auch wirklich
stets zum gewünschten Ergebnis führt.
Zunächst sei also das Verfahren beschrieben (man verfolge die Beschreibung am
besten anhand der Abbildungen). Die Nagelpositionen seien durch eine Menge M
von Punkten gegeben.
Im ersten Schritt betrachte man die konvexe Hülle von M. Die konvexe
Hülle ist die kleinste konvexe2 Menge, die alle Punkte von M
enthält.
Da M eine endliche Menge von Punkten ist, ist dies hier
ein konvexes k-Eck mit
2 ![]() k
k ![]() n (damit wir nicht umständlich Fälle
unterscheiden müssen, bezeichnen wir für k = 2 eine Strecke als Zweieck).
Sei E1 die Menge derjenigen Punkte aus M, die auf
dem Rand dieses k-Ecks liegen (das können durchaus mehr als nur die Ecken
des k-Ecks sein!).
n (damit wir nicht umständlich Fälle
unterscheiden müssen, bezeichnen wir für k = 2 eine Strecke als Zweieck).
Sei E1 die Menge derjenigen Punkte aus M, die auf
dem Rand dieses k-Ecks liegen (das können durchaus mehr als nur die Ecken
des k-Ecks sein!).
Wähle nun zwei beliebige, auf dem Rand des k-Ecks im Uhrzeigersinn
benachbarte Punkte A1 und B1 aus E1 und spanne das (bisher offene)
Gummiband zunächst entlang des k-Ecks von B1 nach A1. Dabei berührt
das Gummiband alle Punkte aus E1. Gibt es nun weitere, noch unberührte
Punkte, ist also
M ![]() E1 nicht leer, so fahre man im zweiten Schritt
mit der Restmenge an Punkten
M2 = (M
E1 nicht leer, so fahre man im zweiten Schritt
mit der Restmenge an Punkten
M2 = (M ![]() E1)
E1) ![]() {A1, B1} fort.
{A1, B1} fort.
Allgemein verfährt man nun im i-ten Schritt (i ![]() 2) folgendermaßen:
Betrachte alle
Punkte Ei auf dem Rand der konvexen Hülle von Mi. Insbesondere sind
Ai-1 und Bi-1 auf dem Rand. Wähle zwei im Uhrzeigersinn
benachbarte Punkte Ai und Bi auf diesem Rand, wobei
{Ai, Bi}
2) folgendermaßen:
Betrachte alle
Punkte Ei auf dem Rand der konvexen Hülle von Mi. Insbesondere sind
Ai-1 und Bi-1 auf dem Rand. Wähle zwei im Uhrzeigersinn
benachbarte Punkte Ai und Bi auf diesem Rand, wobei
{Ai, Bi} ![]() {Ai-1, Bi-1} sein soll. Dies ist stets möglich,
weil der
Rand von Mi mehr als zwei Punkte enthält. Spanne das Gummiband weiter von
Bi-1 entlang des Randes der konvexen Hülle von Mi bis zum Punkt Ai
und
(das andere offene Ende des Bandes) gegen den Uhrzeigersinn von
Ai-1 bis Bi.
Gibt es jetzt noch weitere, unberührte Punkte,
so fahre im nächsten Schritt mit der Menge
Mi+1 = (Mi
{Ai-1, Bi-1} sein soll. Dies ist stets möglich,
weil der
Rand von Mi mehr als zwei Punkte enthält. Spanne das Gummiband weiter von
Bi-1 entlang des Randes der konvexen Hülle von Mi bis zum Punkt Ai
und
(das andere offene Ende des Bandes) gegen den Uhrzeigersinn von
Ai-1 bis Bi.
Gibt es jetzt noch weitere, unberührte Punkte,
so fahre im nächsten Schritt mit der Menge
Mi+1 = (Mi ![]() Ei)
Ei) ![]() {Ai, Bi} fort.
{Ai, Bi} fort.
Gibt es keine unberührten Punkte mehr, dann verbinde Ai mit Bi und
schließe somit das Gummiband.
An welcher Seite der Nägel das Band jeweils herumgeführt werden muss, ergibt
sich automatisch.
Da sich in jedem Schritt die Menge der vom Gummiband noch nicht berührten
Punkte um wenigstens eins verringert, endet das Verfahren irgendwann mit einem
geschlossenen Gummiband, das alle Punkte berührt.
Da die konvexe Hülle von Mi bis auf die Strecke
Ai-1Bi-1 echt im
Inneren der konvexen Hülle von Mi-1 liegt, kommt es beim beschriebenen
Verfahren auch nie zu Überschneidungen das Gummibandes. Demnach endet das
Verfahren stets mit dem gewünschten Ergebnis.
Aufgabe 4
Welche Paare (x, y) reeller Zahlen erfüllen die Gleichung
Erste Lösung:
Angenommen, ein Paar (x, y) erfüllt die Gleichung. Dann gilt sicher auch
bzw. nach Quadrieren
und hieraus folgt nach Quadrieren
Der Übersichtlichkeit halber kann und sollte man alle Terme auf eine Seite bringen und erhält
Aber Achtung! Nicht jedes Paar (x, y) mit y =
Jedes Paar (x, y) mit y =
Analog ist ein Paar (x, y) mit y =
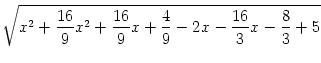 =
= Wir haben also gezeigt, dass genau die Paare (x,
Macht man übrigens die Probe durch Einsetzen, so erhält man auf der linken
Seite den Ausdruck
| /3 |
|||
= 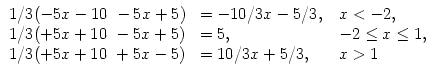 |
und ebenso die Lösung.
Zweite Lösung:
Eine elegante Variante zur Lösung erhalten wir mit geometrischen
Überlegungen:
Die gegebene Gleichung ist äquivalent zu
Fußnoten
- ...1
- von David Wells (Fischer Taschenbuch, 1990)
- ... konvexe2
- Eine Menge von Punkten in der Ebene heißt konvex, wenn sie für jedes Paar A, B von Punkten in M auch die gesamte Strecke AB zwischen diesen Punkten enthält. Die Menge enthält also keine Löcher oder Einbuchtungen.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
