Beispiellösungen zu Aufgabenblatt 42

aktualisiert: 24. April 2005

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1


Denke dir eine beliebige Zahl, in der die Einerziffer größer als alle anderen Ziffern ist und in der die Ziffern von links nach rechts an keiner Stelle kleiner werden. Solche Zahlen sind zum Beispiel 567 oder auch 11122345558.

Multipliziere die von dir gedachte Zahl mit 9, ziehe 1 ab und bilde die Quersumme der erhaltenen Zahl. Multipliziere das Ergebnis mit 5 und addiere 2.

Was ist das Ergebnis? Erhält man immer dieses Ergebnis?


Lösung:


Rechnen wir zunächst ein Beispiel: Die gedachte Zahl sei 567. Dann ist als Erstes 9 . 567 - 1 = 5102 zu berechnen und anschließend die Quersumme, also 5 + 1 + 0 + 2 = 8 zu bestimmen. Daraus resultiert als Ergebnis 8 . 5 + 2 = 42.

Im Folgenden wird gezeigt, dass tatsächlich stets 42 das Ergebnis ist. Betrachten wir hierzu eine beliebige positive ganze Zahl n der geforderten Art, also in Dezimaldarstellung

n = ak . 10k +...+ a1 . 10 + a0    mit    1 $\displaystyle \leq$ ak $\displaystyle \leq$ ak-1 $\displaystyle \leq$...$\displaystyle \leq$ a1 < a0 $\displaystyle \leq$ 9.

Unter Verwendung von 9ai = 10ai - ai gilt dann

9 . n - 1 = (ak) . 10k+1 + (- ak + ak-1) . 10k + (- ak-1 + ak-2) . 10k-1 +...    
  + (- a2 + a1) . 102 + (- a1 + a0) . 10 + (- a0 - 1)    
= (ak) . 10k+1 + (ak-1 - ak) . 10k +...+ (a1 - a2) . 102    
  + (a0 - a1 - 1) . 10 + (10 - a0 - 1).    

Die Zahlen in Klammern in den letzten beiden Zeilen sind hierbei aufgrund der Bedingung an die ai Zahlen von 0 bis 9, es handelt sich also um die Dezimaldarstellung von 9 . n - 1. Somit ist die Quersumme von 9 . n - 1 gegeben durch

ak + (ak-1 - ak) +...+ (a1 - a2) + (a0 - a1 - 1) + (10 - a0 - 1) = 8.

Deswegen ist das Ergebnis der weiteren Rechnung stets 5 . 8 + 2 = 42.


Aufgabe 2


Gegeben seien 180 verschiedene Punkte in der Ebene. Zeige, dass es unter ihnen drei Punkte A, B, C so gibt, dass $ \angle$ABC $ \leq$ 1o ist.


Lösung:


Wir können offenbar annehmen, dass keine drei Punkte auf einer gemeinsamen Geraden liegen, da sonst diese drei Punkte in geeigneter Reihenfolge einen Winkel von 0o einschließen.

Die konvexe Hülle der 180 gegebenen Punkte ist ein k-Eck mit k $ \leq$ 180; denn schließlich können einige der 180 Punkte auch im Inneren des von den übrigen Punkten gebildeten konvexen Vielecks liegen.

Die Innenwinkelsumme in diesem k-Eck ist bekanntlich (k - 2) . 180o. Nach Schubfachprinzip gibt es demnach wenigstens einen der k Innenwinkel, der kleiner oder gleich $ {\frac{{k-2}}{{k}}}$ . 180o groß ist. Sei A der zu diesem Innenwinkel gehörige Eckpunkt des k-Ecks und seien P1, P2,..., P179 die übrigen Punkte in der Reihenfolge, wie sie ein von A aus verlaufender Strahl überstreichen würde; da keine drei Punkte kollinear sind, ist diese Reihenfolge eindeutig. Dann ist, wiederum nach Schubfachprinzip, wenigstens einer der n - 2 Winkel PiAPi+1 für 1 $ \leq$ i $ \leq$ 178 kleiner oder gleich $ {\frac{{1}}{{178}}}$ . $ {\frac{{k-2}}{{k}}}$ . 180o $ \leq$ $ {\frac{{1}}{{178}}}$ . $ {\frac{{178}}{{180}}}$ . 180o = 1o. Hierbei wurde benutzt, dass der Bruch $ {\frac{{k-2}}{{k}}}$ = 1 - $ {\frac{{2}}{{k}}}$ für wachsendes k immer größer wird. Somit haben wir einen gesuchten Winkel gefunden.


Aufgabe 3


Die Oberfläche des Planeten Omega hat die Form eines Torus und ist durch 582 Breitenkreise (im Bild vorn waagerecht) und 2004 Längenkreise (im Bild vorn senkrecht) in Bezirke eingeteilt.

\includegraphics[clip, width=6.5cm]{torus3.eps}
In einigen Bezirken sollen neue Rundfunkstationen errichtet werden, wobei allerdings darauf geachtet werden muss, dass keine zwei Stationen in Bezirken errichtet werden, die zwischen den gleichen zwei benachbarten Breiten- oder Längenkreisen liegen. Außerdem dürfen keine zwei Stationen durch einen diagonalen Weg, also einen Weg, der ausgehend von einem Bezirk stets durch den rechts oben (bzw. rechts unten, links oben oder links unten) benachbarten Bezirk verläuft, verbunden sein.

Wie viele Bezirke mit neuen Rundfunkstationen kann es auf Omega höchstens geben?


Lösung:


Nach den gegebenen Vorschriften können wir nur in 6 Bezirken Rundfunkstationen errichten.


Zunächst zeigen wir, dass wir nicht mehr als 6 Stationen errichten dürfen. Da zwischen zwei Breitenkreisen bzw. zwischen zwei Längenkreisen jeweils nur eine Station stehen darf, ist 582 eine erste Obergrenze für die Anzahl der erlaubten Stationen.

Außerdem darf sich in den Bezirken einer Diagonale auch jeweils nur eine Station befinden. Aber wie viele Diagonalen gibt es überhaupt? Um das herauszufinden, zählen wir erst einmal, wie viele Bezirke zu einer Diagonalen gehören:

Gehen wir von einem Ausgangsfeld immer ein Feld nach rechts oben, so erreichen wir genau nach 582, 2 . 582, 3 . 582, ... Schritten wieder ein Feld, das sich zwischen denselben Breitenkreisen, und genau nach 2004, 2 . 2004, 3 . 2004, ... Schritten ein Feld, das sich zwischen denselben Längenkreisen wie das Ausgangsfeld befindet. Folglich erreichen wir das Ausgangsfeld nach kgV(582, 2004) = 194388 Schritten zum ersten Mal wieder.

Also hat jede Diagonale genau diese Anzahl an Feldern. Da je zwei Diagonalen von links unten nach rechts oben keine gemeinsamen Felder haben (sie sind ,,disjunkt``), gibt es

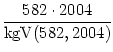$\displaystyle {\frac{{582\cdot 2004}}{{{\mathrm{kgV}}(582, 2004)}}}$ = 6    $\displaystyle \left(\vphantom{ = {\mathrm{ggT}}(582, 2004) }\right.$ = ggT(582, 2004)$\displaystyle \left.\vphantom{ = {\mathrm{ggT}}(582, 2004) }\right)$

solche Diagonalen.


Nun zeigen wir noch ein Beispiel, wie man tatsächlich 6 Stationen auf Omega unterbringen kann. Folgendes 6×12-Rechteck zeigt den Ausschnitt mit Radiostationen auf Omega:


\includegraphics[width=8cm]{l42_3.eps}

Offensichtlich liegen diese 6 Stationen zwischen verschiedenen Breiten- und auch zwischen verschiedenen Längenkreisen. Aber auch die Diagonalregel ist nicht verletzt: Schauen wir uns zwei Felder zwischen zwei benachbarten Breitenkreisen an, so gehören sie genau dann zu ein und derselben Diagonalen, wenn ihr Abstand ein Vielfaches von 6 Feldern ist. Daraus folgt, dass allgemein zwei Felder, deren Abstand in ,,Breitenkreisrichtung`` x Felder und deren Abstand in ,,Längenkreisrichtung`` y Felder beträgt, genau dann auf einer gemeinsamen Diagonalen liegen, wenn x - y oder x + y ein Vielfaches von 6 ist. Dies ist im Bild nie der Fall, die Rundfunkstationen liegen also auf verschiedenen Diagonalen.

Aufgabe 4


In einem Koordinatensystem sind genau alle ganzzahligen Gitterpunkte (a, b) mit 1 $ \leq$ a $ \leq$ 42 und 1 $ \leq$ b $ \leq$ 42 rot gefärbt. Wie viele Quadrate gibt es, deren Eckpunkte sämtlich rot gefärbt sind?


Lösung:


Gesucht waren bei dieser Aufgabe nicht nur die achsenparallelen Quadrate, sondern alle Quadrate, deren Ecken auf den rot gefärbten Punkten liegen. Aber immerhin liegt jedes Quadrat mit Ecken auf den rot gefärbten Punkten passgenau in genau einem achsenparallelen Quadrat mit Ecken auf den gefärbten Gitterpunkten und umgekehrt liegen in einem achsenparallelen Quadrat mit Seitenlänge n genau n solche passgenauen nicht notwendig achsenparallelen Quadrate (siehe Skizze).

Abbildung: Der Fall n = 5
\includegraphics[width=9cm]{l42_4b.eps}

Der linke untere Eckpunkt eines achsenparallelen Quadrates der Seitenlänge n muss aber Koordinaten (a, b) mit 1 $ \leq$ a $ \leq$ 42 - n und 1 $ \leq$ b $ \leq$ 42 - n haben, damit auch alle übrigen Ecken des Quadrates auf gefärbten Punkten liegen. Es gibt also genau (42 - n)2 solche achsenparallelen Quadrate der Seitenlänge n und in jedem von ihnen findet man genau n Quadrate mit Ecken auf den Gitterpunkten. Somit ist die Gesamtzahl an Quadraten mit gefärbten Eckpunkten gleich

$\displaystyle \sum_{{n=1}}^{{41}}$n . (42 - n)2.

Um nicht so viele Zahlen in den Taschenrechner tippen zu müssen, vereinfachen wir die Summe noch weiter - am Ende geht es sogar ohne Rechnerhilfe!

Zuerst fassen wir für 1 $ \leq$ n $ \leq$ 20 jeweils den n-ten und den (42 - n)-ten Summanden zusammen

n(42 - n)2 + (42 - n)n2 = n(42 - n)((42 - n) + n) = 42 . n . (42 - n),

ersetzen dann n = 21 - j und erhalten in der Summe
$\displaystyle \sum_{{n=1}}^{{41}}$n . (42 - n)2 = 213 + $\displaystyle \sum_{{n=1}}^{{20}}$42 . n . (42 - n)  
  = 213 + 42 . $\displaystyle \sum_{{j=1}}^{{20}}$(21 - j)(21 + j).  

Mit der dritten binomischen Formel und der Summenformel für Quadratzahlen, nämlich $ \sum_{{j=1}}^{k}$j2 = $ {\frac{{k(k+1)(2k+1)}}{{6}}}$, ergibt sich nun nacheinander
$\displaystyle \sum_{{n=1}}^{{41}}$n . (42 - n)2 = 213 + 42 . $\displaystyle \sum_{{j=1}}^{{20}}$(21 - j)(21 + j)  
  = 213 + 42 . $\displaystyle \sum_{{j=1}}^{{20}}$(212 - j2)  
  = 213 + 42 . $\displaystyle \left(\vphantom{20 \cdot 21^2 - \sum_{j=1}^{20} j^2}\right.$20 . 212 - $\displaystyle \sum_{{j=1}}^{{20}}$j2$\displaystyle \left.\vphantom{20 \cdot 21^2 - \sum_{j=1}^{20} j^2}\right)$  
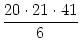  = 213 + 42 . $\displaystyle \left(\vphantom{20 \cdot 21^2 - \frac{20 \cdot 21 \cdot 41}{6}}\right.$20 . 212 - $\displaystyle {\frac{{20 \cdot 21 \cdot 41}}{{6}}}$$\displaystyle \left.\vphantom{20 \cdot 21^2 - \frac{20 \cdot 21 \cdot 41}{6}}\right)$  
  = 213 . (1 + 2 . 20) - 7 . 20 . 21 . 41  
  = 41 . 21 . (212 - 7 . 20)  
  = 861 . 301  
  = 258300 + 861  =  259161.  

Also gibt es genau 259161 Quadrate, deren Ecken auf den rot gefärbten Punkten liegen.

drucken Zum Ausdrucken als pdf-File oder als ps-File