Beispiellösungen zu Aufgabenblatt 43

aktualisiert: 27. Mai 2005

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Aufgabe 1

Finde alle Paare (a, b) von dreistelligen natürlichen Zahlen a und b, für die die sechsstellige Zahl z, die man durch Hintereinanderschreiben von a und b erhält, durch das Produkt a^.b teilbar ist.

Lösung:

Die einzigen Paare dieser Art sind (a, b) = (143, 143) und (a, b) = (167, 334).

Da a und b nach Voraussetzung dreistellig sind, gilt 100 $\leq$ a, b < 1000. Folglich ist die Zahl z, die wir durch das Hintereinanderschreiben von a und b erhalten, z = 1000a + b. Sei nun (a, b) ein solches Paar mit

ab | 1000a + b.

(1)

Als Teiler von ab und von 1000a teilt a dann auch b. Somit gibt es eine ganze Zahl k mit b = ka ; und weil 100 $\leq$ a, b < 1000 ist, ist sogar 1 $\leq$ k < 10. Setzen wir b = ka in (

) ein und teilen durch a, so erhalten wir

aka	\| 1000a + ka = (1000 + k)a
$\displaystyle \Leftrightarrow$ ka	\| 1000 + k.	(2)

Dabei ist ka = b < 1000, so dass ka ein echter Teiler von 1000 + k, d. h. kleiner als diese Zahl ist. Als Teiler von ka und von k teilt k dann auch 1000 und ${\frac{{1000}}{{k}}}$ ist eine ganze Zahl. Teilen der obigen Gleichung (

) durch k ergibt

a | $\displaystyle {\frac{{1000}}{{k}}}$ + 1.

Hier muss wiederum a ein echter Teiler von ${\frac{{1000}}{{k}}}$ + 1 sein. Wegen der beiden Bedingungen 1 $\leq$ k < 10 und k | 1000 brauchen wir nur noch die Werte 1, 2, 4, 5 und 8 für k zu überprüfen.

k	${\frac{{1000}}{{k}}}$ + 1	echte dreistellige Teiler von ${\frac{{1000}}{{k}}}$ + 1
1	1001 = 7^.11^.13	a = 143
2	501 = 3^.167	a = 167
4	251 Primzahl	hat keine echten dreistelligen Teiler
5	201 = 3^.67	hat keine echten dreistelligen Teiler
8	126	hat keine echten dreistelligen Teiler

Folglich sind wegen b = k^.a die beiden einzig möglichen Paare, die die Teilbarkeitsbedingung erfüllen können, (143, 143) und (167, 334).

Eine Probe ergibt, dass z = 143143 = 7^.20449 tatsächlich durch das Produkt 143^.143 = 20449 und z = 167334 = 3^.55778 durch das Produkt 167^.334 = 55778 teilbar ist.

Aufgabe 2

Kann man mehr oder weniger als die Hälfte aller natürlichen Zahlen von 1 bis 10²⁰ als Summe einer Quadratzahl, einer vierten Potenz einer natürlichen Zahl und einer fünften Potenz einer natürlichen Zahl schreiben?
Hinweis: Die Zahl 5 besitzt zum Beispiel die Darstellung 2² + 0⁴ + 1⁵, die Zahl 7 besitzt keine solche Darstellung.

Lösung:

Man kann weniger als die Hälfte aller natürlichen Zahlen von 1 bis 10²⁰ als eine solche Summe schreiben.

Lässt sich die Zahl z $\leq$ 10²⁰ als z = a² + b⁴ + c⁵ mit natürlichen Zahlen a, b, c schreiben, so gilt wenigstens 0 $\leq$ a², b⁴, c⁵ $\leq$ 10²⁰, also

0 $\displaystyle \leq$ a

$\displaystyle \leq$ $\displaystyle \sqrt{{10^{20}}}$ = 10¹⁰,

0 $\displaystyle \leq$ b

$\displaystyle \leq$ $\displaystyle \sqrt[4]{{10^{20}}}$ = 10⁵,

0 $\displaystyle \leq$ c

$\displaystyle \leq$ $\displaystyle \sqrt[5]{{10^{20}}}$ = 10⁴.

Damit nimmt z = a² + b⁴ + c⁵ in dem gewählten Bereich aber höchstens

(10¹⁰	+1)(10⁵ + 1)(10⁴ + 1)
	= 10¹⁹ + 10¹⁵ + 10¹⁴ + 10¹⁰ + 10⁹ + 10⁵ + 10⁴ + 1
	< 10¹⁹ + 7^.10¹⁵ < 10¹⁹ + 10¹⁹ < 5^.10¹⁹ = $\displaystyle {\frac{{1}}{{2}}}$ ^.10²⁰

verschiedene Werte an.

Aufgabe 3

Pablo und Salvador spielen folgendes Spiel:

Pablo zeichnet ein rotes Dreieck auf ein Blatt Papier. Anschließend zeichnet Salvador vier weiße, zu dem roten Dreieck kongruente Dreiecke auf Papier und schneidet sowohl diese als auch das rote Dreieck aus. Diese fünf kongruenten Dreiecke legt er irgendwie auf den Tisch (dabei darf er sie auch seitenverkehrt hinlegen). Anschließend muss Pablo versuchen, die weißen Dreiecke so auf dem Tisch zu verschieben (ohne sie zu drehen!), dass sie das rote Dreieck, welches nicht bewegt werden darf, vollständig abdecken.

Zeige, dass Pablo das Spiel gewinnen kann, ganz egal wie Salvador spielt!

Gewinnt Pablo auch noch, wenn Salvador die Form des roten Dreiecks auswählen darf?

Lösung:

Wenn Pablo mit Sicherheit gewinnen will, zeichnet er am besten ein gleichseitiges Dreieck auf das Blatt Papier. Denn so ein gleichseitiges Dreieck hat ein paar schöne Eigenschaften: Wie jedes Dreieck lässt es sich in vier zu sich selbst ähnliche Dreiecke zerlegen, die folglich die halbe Kantenlänge haben. Das Schöne ist, dass der Inkreis des großen gleichseitigen Dreiecks genauso groß wie der Umkreis eines der kleinen Dreiecke ist. Da der Inkreis eines Dreiecks nach Definition vollständig im Inneren des Dreiecks liegt, kann Pablo also gewinnen, indem er die vier weißen Dreiecke so legt, dass ihre Inkreise mit den Umkreisen der vier Teildreiecke zusammenfallen. Damit hat er dann das rote Dreieck vollständig überdeckt.

$\includegraphics[width=5cm]{l43_32.eps}$
Abdeckung eines der Teildreiecke durch ein weißes Dreieck

Wenn hingegen Salvador die Form des roten Dreiecks bestimmen darf, so kann er gewinnen; zum Beispiel kann er ein gleichschenkliges Dreieck zeichnen, dessen Höhe über der Basis fünfmal so lang ist wie die Basis selbst. Wenn er dann die weißen Dreiecke quer zum roten legt, kann Pablo mit ihnen das rote nicht überdecken, denn in Richtung der Höhe des roten Dreiecks kann man mit den vier weißen Dreiecken zusammen maximal eine Ausdehnung hinbekommen, die viermal so lang ist wie die Basis; aber nach Salvadors Wahl ist die Höhe des roten Dreiecks fünfmal so lang wie seine Basis.

$\includegraphics[]{l43_33.eps}$
Beispiel zur Gewinnstrategie von Salvador

Aufgabe 4

In dem alten buddhistischen Kloster Wan-Dan (nahe Hanoi) beschäftigen sich die Mönche seit alters her mit einem heiligen Brauch:

Sie haben 2000 Edelsteine zur Verfügung, die sich alle voneinander unterscheiden. Zu Beginn des Ritus wird an einem Morgen eine gerade Anzahl 2n von Steinen ausgewählt. Sodann werden, um zugleich die Vielfältigkeit und die Ausgewogenheit der Welt zu versinnbildlichen, die 2n Steine in andächtiger Ruhe dreimal täglich, am Morgen, am Mittag und am Abend, auf eine kupferne und eine irdene Schale aufgeteilt, und zwar so, dass in jede Schale n Steine kommen.

Hierbei wird strengstens darauf geachtet, dass jede mögliche Verteilung der Steine auf die beiden Schalen im Laufe des Rituals genau einmal vorkommt. Für die Zukunft des Klosters ist nun entscheidend, wann das Ende des Rituals erreicht wird: Geschieht es des Abends, so verheißt die Zukunft Gutes. Ansonsten aber droht schweres Unheil.

Für wie viele Zahlen 2n an gewählten Edelsteinen mit 1 $\leq$ n $\leq$ 1000 können die Mönche beruhigt in die Zukunft blicken?

Lösung:

Zuerst berechnen wir, wie viele Möglichkeiten es bei gegebenem n gibt, die 2n Edelsteine auf die beiden Schalen zu verteilen (wer schon mit Binomialkoeffizienten gearbeitet hat, kann den nachfolgenden Abschnitt getrost überspringen):

Es gibt 2n^.(2n - 1)^....^.(n + 2)^.(n + 1) = ${\frac{{(2n)!}}{{n!}}}$ Möglichkeiten (mit k! wird das Produkt k^.(k - 1)^....^.2^.1 bezeichnet), aus den 2n Steinen n Stück auszuwählen und in eine Reihe zu legen: Für die Wahl des ersten Steines gibt es 2n Möglichkeiten, für die Wahl des zweiten nur noch 2n - 1 usw., und für den n-ten Stein schließlich noch n + 1. Legen wir die n Steine in eine Schale, so ist die Reihenfolge, in der wie sie gezogen hatten, nicht mehr wichtig. Vielmehr ergeben alle Anordnungen dieser n Steine dieselbe Schalenverteilung. Dafür gibt es nach demselben Prinzip wie oben genau n^.(n - 1)^....^.2^.1 = n! Möglichkeiten.

Insgesamt gibt es damit genau ${\frac{{(2n)!}}{{n!\cdot n!}}}$ mögliche Verteilungen der Steine auf die beiden Schalen. Der Mathematiker bezeichnet diese Zahl mit $\binom{2n}{n}$ und nennt sie den Binomialkoeffizient ,,2n über n``.

Somit müssen sich die Mönche genau dann keine Sorgen machen, wenn $\binom{2n}{n}$ durch 3 teilbar ist. Für welche n ist dies nun der Fall?

Um dies herauszufinden, überlegen wir uns zunächst, wie viele Primfaktoren 3 in der Zahl n! enthalten sind. Allgemein sei v₃(k) die Anzahl der Primfaktoren 3 in der Primfaktorzerlegung der natürlichen Zahl k. Unter Benutzung der ,,Abrunden``-Funktion $\lfloor$ . $\rfloor$ kann man dann feststellen, dass genau $\lfloor$ n/3 $\rfloor$ der n Faktoren in n! durch 3 teilbar sind, also einen oder mehrere Primfaktoren 3 enthalten. Genau $\lfloor$ n/9 $\rfloor$ wiederum enthalten mindestens zwei Primfaktoren 3 und allgemein enthalten genau $\lfloor$ n/3^k $\rfloor$ der Faktoren mindestens k Primfaktoren 3. Damit erhält man

v₃(n!) = $\displaystyle \lfloor$ n/3 $\displaystyle \rfloor$ + $\displaystyle \lfloor$ n/9 $\displaystyle \rfloor$ +...+ $\displaystyle \lfloor$ n/3^k $\displaystyle \rfloor$ +...= $\displaystyle \sum_{{k=1}}^{\infty}$ $\displaystyle \lfloor$ n/3^k $\displaystyle \rfloor$ .

Hierbei erstreckt sich die Summe nur scheinbar bis ins Unendliche, denn sobald 3^k > n ist, sind die Summanden ja alle gleich 0. Nun können wir aber auch Folgendes berechnen:

v₃( $\displaystyle \binom{2n}{n}$ )	= v₃((2n)!) - 2^.v₃(n!)
	= $\displaystyle \sum_{{k=1}}^{\infty}$ $\displaystyle \lfloor$ 2n/3^k $\displaystyle \rfloor$ - 2^. $\displaystyle \sum_{{k=1}}^{\infty}$ $\displaystyle \lfloor$ n/3^k $\displaystyle \rfloor$
	= $\displaystyle \sum_{{k=1}}^{\infty}$ $\displaystyle \left(\vphantom{\lfloor 2\cdot(n/3^k)\rfloor-2\cdot \lfloor n/3^k\rfloor}\right.$ $\displaystyle \lfloor$ 2^.(n/3^k) $\displaystyle \rfloor$ - 2^. $\displaystyle \lfloor$ n/3^k $\displaystyle \rfloor$ $\displaystyle \left.\vphantom{\lfloor 2\cdot(n/3^k)\rfloor-2\cdot \lfloor n/3^k\rfloor}\right)$ .

Es bezeichne frac(x) den gebrochenen Anteil der nichtnegativen reellen Zahl x, also frac(x) = x - $\lfloor$ x $\rfloor$ . Dann kann man sich (am besten einfach durch scharfes Hinschauen!) schnell überlegen, dass

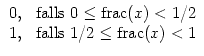
$\displaystyle \lfloor$ 2^.x $\displaystyle \rfloor$ - 2^. $\displaystyle \lfloor$ x $\displaystyle \rfloor$ = $\displaystyle \left\{\vphantom{\begin{array}{l l} 0,& \text{falls } 0\leq {\ma... ...}}(x)<1/2\\ 1,& \text{falls } 1/2\leq {\mathrm{frac}}(x)<1\end{array}}\right.$ $\displaystyle \begin{array}{l l} 0,& \text{falls } 0\leq {\mathrm{frac}}(x)<1/2\\ 1,& \text{falls } 1/2\leq {\mathrm{frac}}(x)<1\end{array}$

gilt. $\binom{2n}{n}$ ist genau dann durch 3 teilbar, wenn v₃( $\binom{2n}{n}$ ) $\geq$ 1 ist, und dies ist also genau dann der Fall, wenn für wenigstens ein k $\geq$ 1 die Ungleichung 1/2 $\leq$ frac(n/3^k) < 1 gilt.

Mit dieser Aussage lässt sich die Aufgabe nun im Prinzip schon lösen, man kann sich durch einen kleinen Trick das Zählen der günstigen n aber noch etwas einfacher machen. Die vielen vorkommenden Dreierpotenzen legen die Betrachtung der Zahlen im Dreiersystem nahe. Wir schreiben nun also unsere Zahl n als

n = a_m^.3^m + a_m-1^.3^m-1 +...+ a₁^.3¹ + a₀ = [a_ma_m-1...a₁a₀]₃,

wobei die a_i jeweils eine der Ziffern 0, 1 oder 2 sind und a_m $\neq$ 0 sein soll. Der Vorteil dieser Schreibweise wird schnell offenbar, denn es ist

n/3^k	=	a_m^.3^m-k + a_m-1^.3^m-k-1 +...+ a_k+1^.3¹ + a_k +
		a_k-1/3 +...+ a₁/3^k-1 + a₀/3^k

und deswegen

frac(n/3^k) = a_k-1/3 +...+ a₁/3^k-1 + a₀/3^k.

Man beachte hierbei, dass der Term auf der rechten Seite kleiner oder gleich s_k : = 2/3 + 2/3² + 2/3³ +...+ 2/3^k ist und man diese Summe recht einfach berechnen kann: Es ist 2s_k = 3s_k - s_k = (2 + 2/3 + 2/3² + 2/3³ +...+ 2/3^k-1) - (2/3 + 2/3² + 2/3³ +...+ 2/3^k) = 2 - 2/3^k, folglich ist s_k < 1.

Wenn nun alle a_i $\in$ {0, 1} sind für 0 $\leq$ i $\leq$ m, dann ist sicher für jedes k

frac(n/3^k)	=	a_k-1/3 +...+ a₁/3^k-1 + a₀/3^k
	$\displaystyle \leq$	1/3 + 1/3² + 1/3³ +...+ 1/3^k = s_k/2 < 1/2.

Ist jedoch a_k-1 = 2, dann ist sicher frac(n/3^k) $\geq$ 2/3 > 1/2.

Daraus schließen wir: $\binom{2n}{n}$ ist genau dann durch 3 teilbar, wenn für wenigstens ein k $\geq$ 1 die Ungleichung 1/2 $\leq$ frac(n/3^k) < 1 gilt, und dies wiederum ist genau dann der Fall, wenn n in seiner Darstellung im Dreiersystem eine Ziffer 2 enthält.

Es ist nun relativ leicht, die Anzahl dieser n zu bestimmen - wir zählen einfach diejenigen n, die keine 2 in ihrer Dreierdarstellung enthalten, und ziehen die erhaltene Anzahl von 1000 ab. Wie viele n zwischen 1 und 1000 haben nun keine 2 in ihrer Dreierdarstellung?

Wegen 1000 = [1101001]₃ gibt es genau die den 105 Binärdarstellungen der Zahlen von 1 bis 105 = [1101001]₂ entsprechenden Dreierdarstellungen von Zahlen n mit der geforderten Eigenschaft. Für alle anderen 1000 - 105 = 895 Zahlen n zwischen 1 und 1000 ist also $\binom{2n}{n}$ durch 3 teilbar und die Mönche können für diese n beruhigt in die Zukunft blicken.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File