Beispiellösungen zu Aufgabenblatt 44

aktualisiert: 18. Juli 2005

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1


Wie oft am Tag stehen der Minuten- und der Stundenzeiger einer Uhr senkrecht aufeinander, und wann geschieht dies nach Mitternacht zum ersten Mal?


Lösung:


In 24 Stunden vollführt der Stundenzeiger zwei, der Minutenzeiger 24 Umdrehungen auf dem Ziffernblatt. Wenn wir die Uhr so mitdrehen, dass der Stundenzeiger immer nach oben zeigt, sieht man folglich (wegen des gleichen Drehsinns) den Minutenzeiger 22 Umdrehungen machen. Während jeder dieser Umdrehungen steht er genau zweimal senkrecht zum Stundenzeiger, nämlich einmal nach rechts und einmal nach links zeigend. Insgesamt stehen die beiden Zeiger also am Tag genau 44-mal senkrecht zueinander.

Beim ersten Senkrechtstand nach Mitternacht hat sich der (schnellere) Minutenzeiger genau um 90 Grad mehr gedreht als der Stundenzeiger. Wir rechnen am einfachsten in Grad und stellen noch fest, dass sich der Minutenzeiger (mg sei sein zurückgelegter Winkel in Grad) genau 12-mal so schnell dreht wie der Stundenzeiger (sg). Die Bedingung für den ersten Senkrechtstand lautet also:

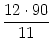mg = sg + 90 = $\displaystyle {\frac{{1}}{{12}}}$mg + 90     $\displaystyle \Longleftrightarrow$     mg = $\displaystyle {\frac{{12\cdot 90}}{{11}}}$ = $\displaystyle {\frac{{1080}}{{11}}}$.

Somit ist der Zeitpunkt des ersten Senkrechtstandes um $ {\frac{{1080}}{{11}}}$ . $ {\frac{{60}}{{360}}}$ min = $ {\frac{{180}}{{11}}}$ min $ \approx$ 16 min 22 sek nach Mitternacht.


Eine andere Möglichkeit, diesen Zeitpunkt zu berechnen, wäre übrigens die folgende: Drehen wir die Uhr nach wie vor so mit, dass der Stundenzeiger immer nach oben zeigt, so brauchen wir nur den Zeitpunkt zu bestimmen, an dem der Minutenzeiger eine Vierteldrehung vollführt hat. Da er sich, wie oben gesehen, in 24 Stunden genau 22-mal dreht, braucht er für diese Vierteldrehung genau $ {\frac{{1}}{{4}}}$ . $ {\frac{{24}}{{22}}}$ = $ {\frac{{3}}{{11}}}$ Stunden, was wieder $ {\frac{{180}}{{11}}}$ Minuten entspricht.


Aufgabe 2


Kirstin und Lars stellen sich zusammen mit 2005 weiteren Kindern im Kreis auf, wobei Kirstin nicht neben Lars steht. Abwechselnd berühren die beiden dann jeweils einen ihrer direkten Nachbarn, worauf dieser Nachbar den Kreis verlassen muss. Gewonnen hat, wer von den beiden als letztes im ,, Kreis`` steht.

Wenn Kirstin beginnt, wer von beiden kann bei klugem Spiel gewinnen?


Lösung:


Kirstin gewinnt, wenn sie klug spielt.

Zwischen Kirstin und Lars stehen insgesamt 2005 Kinder, davon eine gerade Anzahl links von Kirstin und eine ungerade Anzahl rechts oder umgekehrt. Kirstin gewinnt, wenn sie dafür sorgt, dass immer, wenn Lars am Zug ist, auf beiden Seiten eine ungerade Anzahl von Kindern, mindestens also eines zwischen ihnen steht. Folglich wird sie zu Anfang auf der Seite ein Kind berühren, wo die gerade Anzahl von Kindern steht. Wenn Lars nun im Laufe des Spiels seinen rechten Nachbar berührt, fasst Kirstin ihren linken Nachbar an, der ja von Lars aus gesehen rechts steht, so dass dort eine ungerade Anzahl von Kindern übrig bleibt - und entsprechend umgekehrt, wenn Lars seinen linken Nachbarn berührt. So geht es immer weiter, und da in jedem Schritt ein Kind den Kreis verlässt, muss nach spätestens 2004 Schritten Lars einen von Kirstins Nachbarn berühren, woraufhin Kirstin Lars berührt und so das Spiel gewinnt.


Bemerkung: Das Spiel ist, anders als viele andere Spiele, sogar sehr zu Gunsten von Kirstin aufgebaut: Sie muss nicht von Anfang an eine bestimmte Taktik verfolgen, um zu gewinnen. Denn da zu Anfang eine ungerade Zahl von Kindern im Kreis steht, ist dies folglich immer genau dann der Fall, wenn Kirstin wieder an der Reihe ist. Sie kann zunächst sogar ganz beliebig spielen, bis auf einer Seite nur noch ein Kind steht. Sollte Lars dieses berühren, kann sie natürlich im nächsten Schritt gewinnen. Solange sie ihrerseits jedoch dieses Kind nicht berührt, kann sie nicht verlieren, denn auf ihrer anderen Seite wird sie immer eine gerade Zahl von Kindern vorfinden, weil es insgesamt eine ungerade Zahl sein muss. Und damit kann sie dort nicht das letzte Kind durch Berühren herausnehmen, was nötig wäre, damit Lars gewinnt. - Armer Lars!


Aufgabe 3


Olaf schreibt die Zahlen 1 und 2 nebeneinander in eine Reihe. Er berechnet das Produkt 1 . 2 = 2 und fügt die Ziffer 2 hinten an die Reihe an. Danach nimmt Olaf die nächsten beiden Ziffern 2 und 2 und fügt das Produkt 4 wieder hinten an die Reihe an. Im nächsten Schritt erhält Olaf analog die Ziffer 8 und fügt sie an. Danach muss er 4 . 8 = 32 berechnen und die beiden neuen Ziffern 3 und 2 anfügen. Bis dahin hat die entstandene Reihe also die Gestalt

1, 2, 2, 4, 8, 3, 2.

Nun nimmt Olaf wieder das nächste Paar benachbarter Zahlen, deren Produkt noch nicht berechnet wurde, also 8 und 3, und fügt die Ziffern des Produktes 8 . 3 = 24 hinten an die Reihe an. Nach zwei weiteren Schritten hat die Reihe dann die Form

1, 2, 2, 4, 8, 3, 2, 2, 4, 6, 4.

Wenn Olaf die Reihe immer weiter so fortsetzt: An welcher Stelle der Reihe kommt die erste 0 vor? Wo die erste 5, die erste 7 und die erste 9?


Lösung:


Weder die 0 noch die 5, 7 und 9 kommen in der Folge vor. Das sieht man wie folgt ein:

Käme eine der Ziffern 0, 5, 7, 9 vor, so betrachten wir die erste Stelle, an der eine solche Ziffer auftritt. Nach dem Bildungsgesetz müsste diese Ziffer eine Ziffer in einem Produkt von zwei Ziffern sein, die in der Folge vor dieser einen Ziffer stehen. Jedoch ist die einzige Möglichkeit, in einem Produkt von zwei Ziffern der Menge {1, 2, 3, 4, 6, 8} eine der Ziffern 0, 5, 7, 9 zu finden, 3 . 3 = 9 (wie man leicht durch Probieren ermittelt). Es müssten also zwei Dreien in der Folge hintereinander stehen.

Nun gibt es jedoch zu Beginn keine zwei aufeinander folgenden ungeraden Ziffern, und auch nicht nach Anfügen des ersten (geraden!) Produktes. Damit ist jedes Produkt, was aus zwei aufeinander folgenden, bereits bekannten Ziffern gebildet wird, gerade, und weiter entsteht beim Anfügen eines neuen Produktes ebenso kein Paar ungerader Ziffern, denn das Produkt, das höchstens zweistellig ist, wird an eine gerade Ziffer angefügt (die Endziffer des vorigen Produktes) und hat als letzte (genauer: einzige oder zweite) Ziffer eine gerade Ziffer. Damit kann es insbesondere keine zwei Dreien hintereinander geben, so dass die Annahme, es gäbe eine der Ziffern 0, 5, 7, 9 in der Folge, zum Widerspruch geführt wurde.


Aufgabe 4


Die Mönche des Klosters Wan-Dan im nordvietnamesischen Tonking-Gebirge beherbergen in ihrem Gewölbekeller seit Jahrtausenden einen wertvollen
Schatz, nämlich einen riesigen, gläsernen Bergkristall, in dem große Mengen an Gold, Silber und Platin eingeschlossen sind. Einer uralten Prophezeiung zufolge müssen die Weisen des Klosters noch in diesem Jahr den Kristall durch einen einzigen ebenen Schnitt so in zwei Teile teilen, dass in jedem der beiden entstehenden Teile die gleiche Menge an Gold, an Silber und an Platin ist. Sollte der Schnitt nicht eben oder die Edelmetalle nicht gleichmäßig aufgeteilt sein, so droht dem Kloster ewiges Unheil.

Zeige, dass die Mönche ihr Kloster retten können!


Nachtrag zur Aufgabenstellung:

Wir wurden - zu Recht - darauf hingewiesen, dass die Aufgabe manchmal nicht lösbar ist: Es kann nämlich sein, dass es zwar einen ebenen Schnitt gibt, der die Metallanteile halbiert, aber der Kristall durch den Schnitt in mehr als zwei Teile zerfällt (das kann z. B. passieren, wenn der Kristall U-förmig ist).

Gemeint war, dass man nur zeigen sollte, dass es eine Schnittebene wie beschrieben gibt. Entstehen physisch mehr als zwei Teile, ist das kein Vergehen, wir fassen die Teilstücke auf einer jeden Seite zu einem Teil zusammen.


Lösung:


Zunächst stellen wir uns den Kristall als kugelrund vor - dies ändert offenbar nichts an der Aufgabe, denn man kann dies durch Hinzufügen von Kristall erreichen, der für diese Aufgabe nur Füllmaterial ist. (Hier war die Aufgabe eventuell nicht klar genug formuliert: Die beim Zerschneiden entstehenden ,,Teile``sind als ,,Hälften``zu verstehen, und dürfen durchaus auch aus mehreren Einzelteilen bestehen, wenn der Kristall ungünstig geformt ist.)

Der Mittelpunkt dieser Kristallkugel k sei M und r sei ihr Radius.

\includegraphics[]{l44_41iv.eps}

Für jeden Punkt Q auf der Oberfläche von k betrachten wir nun die Tangentialebene EQ an der Kugel in Q (das ist die Ebene, die die Kugel in dem Punkt Q berührt) und verschieben diese gedanklich parallel in Richtung $ \overrightarrow{QM}$, bis sie nach einer Verschiebung um 2r wieder tangential an der Kugel ist. Betrachtet man den Anteil des Goldes, der während dieses Verschiebens auf derselben Seite von EQ wie Q ist, so ist dieser zu Beginn bei 0 Prozent und am Ende bei 100 Prozent.

Da es beim Verschieben keine Sprünge in diesem Anteil geben kann (das Verschieben ist eine stetige Bewegung), muss also irgendwann die Ebene EQ das Gold genau halbieren. Die Streckenlänge, um die man EQ bis dahin verschieben musste, nennen wir dG. Offenbar gilt 0 < dG < 2r.

Ganz analog gilt das natürlich auch für das Silber und das Platin, so dass man auch hier nach Verschieben um dS bzw. dP Ebenen erhält, die parallel zu EQ sind und das Silber bzw. das Platin genau halbieren.

Zu jedem Punkt Q auf der Kugeloberfläche betrachten wir nun das Paar (xQ, yQ) = (dG - dP, dG - dS).

Eine wichtige Beobachtung ist dabei: Wenn - Q den zu Q gegenüberliegenden Punkt auf der Oberfläche von k bezeichnet, so gilt

(x-Q, y-Q) = (- xQ, - yQ).

Dies folgt einfach aus der Tatsache, dass die Ebenen, die Gold, Silber und Platin halbieren, für Q und - Q dieselben sind, man aber in genau entgegengesetzte Richtungen verschieben muss, um diese zu erhalten.

Nun lassen wir Q auf der Oberfläche von k einen Großkreis t (das ist ein Kreis maximalen Radius auf der Kugeloberfläche - wie z. B. der Äquator oder jeder Längenkreis) entlangfahren. Die Punkte (xQ, yQ) beschreiben dabei eine geschlossene Kurve $ \gamma$ in der Koordinatenebene. Zu jedem Punkt (x, y) auf dieser Kurve gehört, wie eben gesehen, auch der am Ursprung (0, 0) gespiegelte Punkt (- x, - y) zur Kurve.

Daraus folgt, dass der Ursprung im Inneren der von der Kurve umschlossenen Fläche liegen muss.

\includegraphics[]{l44_42i.eps}

Nun drehen wir den Großkreis t in Gedanken um 180o um einen seiner Durchmesser und beobachten das Verhalten der Kurve $ \gamma$ dabei. Diese ist, wie eben gesehen, zu jedem Zeitpunkt während dieser Drehung punktsymmetrisch zum Ursprung und die beiden Punkte (xA, yA) und (xB, yB), die zu den Endpunkten A, B der Drehachse gehören, bleiben fest. Da am Ende der Drehung wieder derselbe Großkreis wie zu Beginn vorliegt, erhält man am Ende auch dieselbe Kurve $ \gamma$ wie zu Beginn - wichtig ist aber, dass während der Drehung die beiden Teile der Kurve zwischen (xA, yA) und (xB, yB) die Plätze getauscht haben!

\includegraphics[]{l44_43iv.eps}

Zu irgendeinem Zeitpunkt muss die Kurve also den Ursprung (0, 0) überstrichen haben. Zu dieser Kurve gehört also ein Punkt Q auf der Kugeloberfläche, für den dG - dS = 0 = dG - dP ist. Die drei Ebenen, welche die jeweiligen Materialien halbieren, fallen also für diesen Punkt Q zu einer einzigen zusammen, und wenn die Mönche entlang dieser Ebene schneiden, retten sie ihr Kloster.


Bemerkung 1: Der angegebene Beweis ist, streng mathematisch betrachtet, nicht ganz zufriedenstellend, da er an einigen Stellen zwar offensichtliche, aber in diesem Sinne eben ,,nur`` anschauliche Argumente verwendet. Ein ,,ganz`` exakter Beweis benutzt Begriffe der höheren Mathematik aus dem Bereich der Topologie. Im Kern ist er aber dem oben angegebenem identisch. Benutzt wird meist der Satz von Borsuk-Ulam, welcher, im Spezialfall unseres Beweises, sicherstellt, dass beim Variieren von Q auf der Kugel irgendwann einmal (xQ, yQ) = (0, 0) ist


Bemerkung 2: Etwas anders verpackt findet man die Aussage der Aufgabe auch in vielen Lehrbüchern der Topologie. Dort wird die Aussage oft ,, Ham-Sandwich-Theorem`` genannt. Ins Deutsche übersetzt heißt das so viel wie ,,Satz vom Schinkenbrötchen``. Aufgabe ist es dann, die beiden Hälften eines Brötchens und den dazwischen liegenden Schinken durch einen ebenen Messerschnitt in je zwei gleiche Hälften zu teilen.


Bemerkung 3: Viele Einsender behaupteten, dass jede Ebene, die durch den Schwerpunkt zum Beispiel des Goldanteils verläuft, das Gold auch halbieren muss.

Das ist falsch!

Als einfaches Gegenbeispiel denke man sich den Goldanteil in Form eines regelmäßigen Tetraeders. Ein Schnitt durch dessen Schwerpunkt parallel zu einer Seitenfläche teilt das Tetraeder im Verhältnis 27 : 37.

drucken Zum Ausdrucken als pdf-File oder als ps-File