Beispiellösungen zu Aufgabenblatt 56

aktualisiert: 8. November 2006

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Aufgabe 1

Die drei Musketiere Porthos, Athos und Aramis streiten sich darum, wer in der bevorstehenden Nacht die erste Wache halten muss. Sie beschließen, dies durch Würfeln zu entscheiden: Es wird der Reihe nach gewürfelt und wer als Erster eine Sechs würfelt, muss Wache halten.

Ist das gerecht? Wie groß ist für jeden der drei die Wahrscheinlichkeit, Wache halten zu müssen, wenn sie der alphabetischen Reihenfolge nach würfeln?

Zusatz: Löse das Problem sicherheitshalber auch für die sieben Zwerge, Ali Baba und die vierzig Räuber bzw. gleich allgemein für n Streitende!

Lösung:

Betrachten wir zunächst die drei Musketiere Aramis, Athos und Porthos:

Allgemein beträgt die Wahrscheinlichkeit für eine Sechs beim Werfen eines Würfels ${\frac{{1}}{{6}}}$ , die Wahrscheinlichkeit, keine Sechs zu werfen, ${\frac{{5}}{{6}}}$ .

Also beträgt die Wahrscheinlichkeit, bereits nach der ersten Runde Würfeln Wache halten zu müssen, für Aramis ${\frac{{1}}{{6}}}$ , für Arthos ${\frac{{5}}{{6}}}$ ^. ${\frac{{1}}{{6}}}$ (da dies voraussetzt, dass Aramis zuvor keine Sechs gewürfelt hat) und für Porthos ${\frac{{5}}{{6}}}$ ^. ${\frac{{5}}{{6}}}$ ^. ${\frac{{1}}{{6}}}$ (es dürfen weder Aramis noch Arthos eine Sechs gewürfelt haben). Sollte nach der ersten Runde keiner der drei eine Sechs geworfen haben, so wiederholt sich der Ablauf des Spiels und in der zweiten Runde gelten für jeden wieder die gleichen Wahrscheinlichkeiten, nach dieser Runde Wache halten zu müssen.

Insgesamt kann man also sagen, dass die Wahrscheinlichkeit für Athos ${\frac{{5}}{{6}}}$ -mal so groß und die für Porthos $\left(\vphantom{\frac{5}{6} \cdot \frac{5}{6}}\right.$ ${\frac{{5}}{{6}}}$ ^. ${\frac{{5}}{{6}}}$ $\left.\vphantom{\frac{5}{6} \cdot \frac{5}{6}}\right)$ -mal so groß ist wie die für Aramis, die erste Wache halten zu müssen.

Sei nun mit p die Wahrscheinlichkeit für Aramis bezeichnet. Da die Summe der drei Wahrscheinlichkeiten genau 1 ergeben muss, gilt:

p + $\displaystyle {\frac{{5}}{{6}}}$ ^.p + $\displaystyle {\frac{{5}}{{6}}}$ ^. $\displaystyle {\frac{{5}}{{6}}}$ ^.p	= 1 oder zusammengefasst
$\displaystyle {\frac{{91}}{{36}}}$ ^.p	= 1 und damit
p	= $\displaystyle {\frac{{36}}{{91}}}$ $\displaystyle \approx$ 0, 3956 = 39, 56%.

Die Wahrscheinlichkeiten für Aramis, Athos und Porthos sind also

$\displaystyle {\frac{{36}}{{91}}}$ $\displaystyle \approx$ 39, 56%, $\displaystyle {\frac{{36}}{{91}}}$ ^. $\displaystyle {\frac{{5}}{{6}}}$ = $\displaystyle {\frac{{30}}{{91}}}$ $\displaystyle \approx$ 32, 97% und $\displaystyle {\frac{{36}}{{91}}}$ ^. $\displaystyle {\frac{{5}}{{6}}}$ ^. $\displaystyle {\frac{{5}}{{6}}}$ = $\displaystyle {\frac{{25}}{{91}}}$ $\displaystyle \approx$ 27, 47%

Das Spiel ist nicht gerecht.

Für n Streitende lösen wir das Problem analog:

Sei wieder p die Wahrscheinlichkeit, dass der erste in der Runde zuerst Wache halten muss. Dann gilt:

p + $\displaystyle {\frac{{5}}{{6}}}$ ^.p + $\displaystyle \left(\vphantom{ \frac{5}{6} }\right.$ $\displaystyle {\frac{{5}}{{6}}}$ $\displaystyle \left.\vphantom{ \frac{5}{6} }\right)^{2}_{}$ ^.p +...+ $\displaystyle \left(\vphantom{ \frac{5}{6} }\right.$ $\displaystyle {\frac{{5}}{{6}}}$ $\displaystyle \left.\vphantom{ \frac{5}{6} }\right)^{{n-1}}_{}$ ^.p	= 1, das heißt (*)
p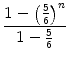^. $\displaystyle {\frac{{1-\left( \frac{5}{6} \right) ^n}}{{1-\frac{5}{6}}}}$	= 1 bzw.
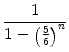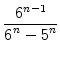p	= $\displaystyle {\frac{{1}}{{6}}}$ ^. $\displaystyle {\frac{{1}}{{1-\left( \frac{5}{6} \right) ^n}}}$ = $\displaystyle {\frac{{6^{n-1}}}{{\displaystyle 6^{n} - 5^{n}}}}$ .

Für den i-ten Streitenden der Würfelreihenfolge ergibt sich dann eine Wahrscheinlichkeit von

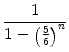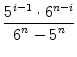p_i = $\displaystyle {\frac{{1}}{{6}}}$ ^. $\displaystyle \left(\vphantom{ \frac{5}{6} }\right.$ $\displaystyle {\frac{{5}}{{6}}}$ $\displaystyle \left.\vphantom{ \frac{5}{6} }\right)^{{i-1}}_{}$ ^. $\displaystyle {\frac{{1}}{{1-\left( \frac{5}{6} \right) ^n}}}$ = $\displaystyle {\frac{{5^{i-1}\cdot 6^{n-i}}}{{\displaystyle 6^n-5^n}}}$ .

Bemerkung: An der mit (*) markierten Stelle haben wir einen Rechentrick, nämlich die Formel für die endliche geometrische Reihe benutzt, welche man sich wie folgt überlegen kann:

Sei s = 1 + $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)$ + $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)^{{2}}_{}$ +...+ $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)^{{n-1}}_{}$ . Dann ist ${\frac{{5}}{{6}}}$ ^.s = $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)$ + $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)^{{2}}_{}$ +...+ $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)^{{n}}_{}$ . 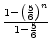Diese Gleichungen subtrahiert man nun und erhält: $\left(\vphantom{1-\frac{5}{6} }\right.$ 1 - ${\frac{{5}}{{6}}}$ $\left.\vphantom{1-\frac{5}{6} }\right)$ ^.s = 1 - $\left(\vphantom{ \frac{5}{6} }\right.$ ${\frac{{5}}{{6}}}$ $\left.\vphantom{ \frac{5}{6} }\right)^{{n}}_{}$ , alsos = ${\frac{{1- \left( \frac{5}{6} \right) ^{n}}}{{1-\frac{5}{6}}}}$

Aufgabe 2

Auf einem Blatt Papier ist ein großes rotes gleichseitiges Dreieck gezeichnet. Malte hat einen Vorrat grüner Papierstücke, die alle gleich groß sind und ebenfalls alle die Form eines gleichseitigen Dreiecks haben. Er nimmt fünf davon und legt sie so auf das rote Dreieck, dass sie dieses vollständig abdecken.

Zeige, dass Malte dies auch schon mit vier grünen Dreiecken geschafft hätte.

Lösung:

Sei mit a die Seitenlänge des roten und mit b die der grünen Dreiecke bezeichnet.

Wir nehmen nun an, dass b < ${\frac{{a}}{{2}}}$ ist: Da mit den grünen Dreiecken das rote vollständig bedeckt werden soll, müssen insbesondere auch die drei Ecken und die drei Seitenmitten des roten Dreiecks bedeckt werden. In einem Dreieck der Seitenlänge a haben je zwei Seitenmitten und somit auch je zwei der sechs genannten Punkte einen Abstand von mindestens ${\frac{{a}}{{2}}}$ . Deshalb kann ein grünes Dreieck, das einen dieser Punkte bedeckt, keinen weiteren der Punkte bedecken. Man benötigt in diesem Fall also mindestens sechs grüne Dreiecke.

Aus der Tatsache, dass für Malte schon fünf Dreiecke ausreichend sind, folgt, dass b $\geq$ ${\frac{{a}}{{2}}}$ ist.

Da man durch Verbinden der Seitenmittelpunkte das rote Dreieck in vier gleichseitige Dreiecke der Seitenlänge ${\frac{{a}}{{2}}}$ zerteilen kann, folgt direkt, dass Malte das rote auch mit vier der grünen Dreiecke bedecken kann.

Aufgabe 3

Bei einer Mathematikarbeit stellte der Lehrer den Schülern zehn Fragen, die jeweils mit ,,wahr`` (w) oder ,,falsch`` (f) beantwortet werden sollten. Für eine richtige Antwort gab es einen Punkt, für eine falsche keinen Punkt. Ingo, Stephan, Elias und Jörg beantworteten die Fragen wie folgt:

Name	1	2	3	4	5	6	7	8	9	10
Ingo	w	w	w	f	w	w	f	f	w	w
Stephan	f	w	f	w	w	f	f	f	f	f
Elias	w	f	f	w	f	f	w	f	w	f
Jörg	w	w	f	w	w	f	f	w	w	f

Bei der Rückgabe der Arbeiten bekommt zuerst Ingo seine Arbeit wieder und erhält 6 Punkte, Stephan bekommt 8 Punkte und Elias erhält 7 Punkte.

Wie viele Punkte wird Jörg wohl bekommen?

Lösung: Wenn man sich die ersten drei Zeilen der Tabelle genau ansieht, so erkennt man, dass sich Ingo, Stephan und Elias nur bei Frage 8 einig waren und demnach bei allen neun anderen Fragen wenigstens einer der drei falsch geantwortet hat. Somit konnten die drei zusammen nicht mehr als 3^.10 - 9 = 21 Punkte erhalten. Da 6 + 7 + 8 = 21 ist, sie also tatsächlich genau diese maximale Punktanzahl erhielten, müssen sie (zusammen) bei jeder Frage außer Frage 8 genau einen Punkt verloren und bei Frage 8 gar keinen Punkt verloren haben. Demnach ist die richtige Antwort auf jede Frage genau diejenige, für die sich die Mehrheit der drei entschieden hat:

Aufgabe	1	2	3	4	5	6	7	8	9	10
richtige Antwort	w	w	f	w	w	f	f	f	w	f

Vergleicht man dies mit Jörgs Antworten, so sieht man, dass er sich nur bei Frage 8 geirrt hat und daher genau 9 Punkte erhalten wird.

Aufgabe 4

Peter zeichnet zwei Sehnen in einen Kreis und stellt fest, dass diese sich gegenseitig halbieren. Zeige, dass Peter zwei Durchmesser gezeichnet haben muss.

Nun zeichnet Peter zwei Sehnen in eine Ellipse, und wieder halbieren sich diese gegenseitig. Muss es sich auch diesmal um Sehnen handeln, die durch den Mittelpunkt der Ellipse gehen?

Lösung:

Seien AC und BD die beiden Sehnen, die sich im Punkt S schneiden und sich gegenseitig halbieren. Dann ist zum einen | AS| = | CS| und | BS| = | DS| und zum anderen $\angle$ ASB = $\angle$ CSD und $\angle$ BSC = $\angle$ DSA. Nach Kongruenzsatz sws sind die Dreiecke ABS und CDS sowie die Dreiecke BCS und DAS also kongruent. Insbesondere heißt das aber, dass | AB| = | CD| und | BC| = | DA| ist. Das Viereck ABCD ist daher ein Parallelogramm.

$\includegraphics[width=50mm]{loes56_4}$
Skizze (eines Falles, der letztlich falsch ist)

In einem Parallelogramm sind die Innenwinkel in gegenüberliegenden Ecken gleich groß (nach Wechselwinkelsatz). Da es sich bei dem Parallelogramm ABCD aber auch um ein Sehnenviereck handelt, ergänzen sich gegenüberliegende Winkel auch zu 180^o. Daraus folgt, dass jeder Innenwinkel gleich 90^o sein muss. Das Viereck ABCD ist also sogar ein Rechteck.

Daraus folgt dann aber schließlich nach der Umkehrung des Satzes des Thales, dass die beiden Sehnen AC und BD Durchmesser des Kreises sein müssen.

Auch bei einer Ellipse können sich zwei Sehnen nur halbieren, wenn sie durch den Mittelpunkt der Ellipse gehen. Um dies einzusehen, wenden wir einen kleinen Trick an. Legt man die Ellipse E so in ein Koordinatensystem, dass der Mittelpunkt im Ursprung und die große Halbachse auf der x-Achse liegt, so hat sie bekanntlich die Gleichung

$\displaystyle {\frac{{x^2}}{{a^2}}}$ + $\displaystyle {\frac{{y^2}}{{b^2}}}$ = 1,

wobei a und b die Längen der großen und kleinen Halbachsen sind. Wir wenden nun auf die Ellipse die folgende Abbildung an:

f : (x, y) $\displaystyle \mapsto$ (x, $\displaystyle {\frac{{a}}{{b}}}$ y).

Diese Abbildung streckt also gewissermaßen das ganze Koordinatensystem in y-Richtung.

Wichtig ist dabei folgendes: Ist M der Mittelpunkt der Strecke AB, so ist f (M) der Mittelpunkt der Strecke f (A)f (B).

Dies sieht man schnell ein, denn sind M = (x_M, y_M), A = (x_A, y_A) und B = (x_B, y_B) die Koordinaten der beteiligten Punkte, so gilt, wenn M Mittelpunkt von AB ist,

x_M = $\displaystyle {\frac{{1}}{{2}}}$ (x_A + x_B) und y_M = $\displaystyle {\frac{{1}}{{2}}}$ (y_A + y_B).

Dann ist aber auch

x_f(M) = x_M = $\displaystyle {\frac{{1}}{{2}}}$ (x_A + x_B) = $\displaystyle {\frac{{1}}{{2}}}$ (x_f(A) + x_f(B))

und

y_f(M) = $\displaystyle {\frac{{a}}{{b}}}$ y_M = $\displaystyle {\frac{{1}}{{2}}}$ ( $\displaystyle {\frac{{a}}{{b}}}$ y_A + $\displaystyle {\frac{{a}}{{b}}}$ y_B) = $\displaystyle {\frac{{1}}{{2}}}$ (y_f(A) + y_f(B)).

Also ist tatsächlich f (M) der Mittelpunkt von f (A) und f (B).

Außerdem ist das Bild der Ellipse E unter der Abbildung f ein Kreis mit Radius a und Mittelpunkt im Ursprung (0, 0), denn der Punkt (x, y) liegt genau dann auf der Ellipse, wenn

$\displaystyle {\frac{{x^2}}{{a^2}}}$ + $\displaystyle {\frac{{y^2}}{{b^2}}}$ = 1

ist, wenn also

x² + $\displaystyle \left(\vphantom{\frac{a}{b}y}\right.$ $\displaystyle {\frac{{a}}{{b}}}$ y $\displaystyle \left.\vphantom{\frac{a}{b}y}\right)^{2}_{}$ = a²

ist. Das ist aber genau dann der Fall, wenn f (x, y) auf dem Kreis X² + Y² = a² liegt.

Nun ist der eigentliche Beweis nicht mehr schwer. Seien AC und BD zwei Sehnen in der Ellipse E, die sich in S schneiden und sich gegenseitig halbieren. Dann wenden wir die Abbildung f auf die gesamte Konstellation an und sehen, dass f (A)f (C) und f (B)f (D) zwei Sehnen im Kreis f (E) sind, die sich in f (S) schneiden und sich immer noch gegenseitig halbieren (weil f (S) immer noch Mittelpunkt beider Sehnen ist). Wie im ersten Teil der Aufgabe bewiesen, muss dann aber notwendig f (S) = (x_S, ${\frac{{a}}{{b}}}$ y_S) = (0, 0) (der Mittelpunkt des Kreises f (E)) sein. Daraus folgt aber sofort, dass schon S selbst der Koordinatenursprung und damit der Mittelpunkt der Ellipse E war.

Bemerkung: Sehr erfreut hat uns an Euren eingesandten Lösungen der Aufgabe, dass es sehr viele verschiedene (erfolgreiche) Ansätze gab: Wir kennen jetzt sechs wesentlich verschiedene Lösungen. Eine weitere Lösung sei im Folgenden skizziert (nach Daniel Luckhardt). Die anderen Lösungen verwendeten geeignet gewählte Koordinaten und die Kreisgleichung, den Sehnensatz, betrachteten die Mittelsenkrechten der Sehnen oder zeigten, dass es zu jedem Punkt außer dem Mittelpunkt im Inneren einer Ellipse genau eine Sehne gibt, die ihren Mittelpunkt auf diesem Punkt hat.

2. Lösung:

Sei AB eine Sehne im Kreis, deren Mittelpunkt S sei. Angenommen, es gebe eine andere Sehne CD, die durch S halbiert werde. Die Figur aus den beiden Sehnen ist dann punktsymmetrisch um den Punkt S.

Nun werde auch der Kreis an dem Punkt S gespiegelt. Da die Punkte A, B, C und D nach Voraussetzung bei der Punktspiegelung in dieser Reihenfolge auf die Punkte B, A, D und C abgebildet werden, hat der Bildkreis mit dem originalen Kreis vier verschiedene Punkte gemeinsam. Das geht nur, wenn die beiden Kreise identisch sind, und das heißt, dass S mit dem Kreismittelpunkt zusammenfallen muss.

Diese Argumentation lässt sich sogar auch für Ellipsen anwenden, denn das Bild einer Ellipse unter einer Punktspiegelung (Drehung um 180^o) ist eine dazu kongruente Ellipse, deren Halbachsen parallel zu denen der originalen Ellipse sind. Und zwei verschiedene solche Ellipsen können ebenfalls nur zwei Schnittpunkte haben, wie man sich überlegen kann.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File