Beispiellösungen zu Aufgabenblatt 63

aktualisiert: 4. September 2007

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

ACHTUNG: Diese HTML-Version der Lösung wird nicht ganz korrekt angezeigt. Bitte die PDF- oder PS-Version benutzen!

Aufgabe 1

Sieben Zwerge graben sieben Tage lang täglich sieben Stunden an einem Tunnel durch den Berg und kommen dabei insgesamt sieben Meter vorwärts.

Zwerg Frosti wird krank, und da man sich um ihn kümmern muss, wird die Arbeitszeit aller Zwerge um eine Stunde verkürzt.

In den nächsten sechs Tagen graben also nur noch sechs Zwerge sechs Stunden täglich an dem Tunnel und kommen dabei ... ja, wie weit kommen die Zwerge dabei dann eigentlich vorwärts?

Lösung:

Wir bestimmen die Arbeit (hier in Metern gemessen), die ein Zwerg in einer Stunde verrichtet:

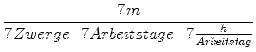$\displaystyle {\frac{{7 m}}{{7 Zwerge \cdot 7 Arbeitstage \cdot 7 \frac{h}{Arbeitstag}}}}$ = $\displaystyle {\frac{{1}}{{49}}}$ $\displaystyle {\frac{{m}}{{Zwerg \cdot h}}}$

Somit schaffen sechs Zwerge in sechs Tagen, an denen sie je sechs Stunden arbeiten,

6^.6^.6^. $\displaystyle {\frac{{1}}{{49}}}$ = $\displaystyle {\frac{{216}}{{49}}}$ = 4 ${\frac{{20}}{{49}}}$ $\displaystyle \approx$ 4, 41 Meter.

Aufgabe 2

Finde ganze Zahlen a, b und c so, dass

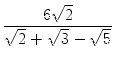$\displaystyle {\frac{{6\sqrt{2}}}{{\sqrt{2}+\sqrt{3}-\sqrt{5}}}}$ = a + $\displaystyle \sqrt{{b}}$ + $\displaystyle \sqrt{{c}}$

gilt.

Lösung:

Durch Erweitern des Terms ${\frac{{6\sqrt{2}}}{{\sqrt{2}+\sqrt{3}-\sqrt{5}}}}$ nach der dritten binomischen Formel erhält man:

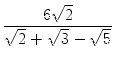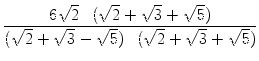$\displaystyle {\frac{{6\sqrt{2}}}{{\sqrt{2}+\sqrt{3}-\sqrt{5}}}}$	= $\displaystyle {\frac{{6\sqrt{2}\cdot(\sqrt{2}+\sqrt{3}+\sqrt{5})}}{{(\sqrt{2} + \sqrt{3} - \sqrt{5})\cdot(\sqrt{2}+\sqrt{3}+\sqrt{5})}}}$
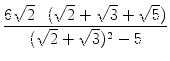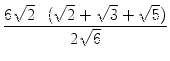	= $\displaystyle {\frac{{6\sqrt{2}\cdot(\sqrt{2}+\sqrt{3}+\sqrt{5})}}{{(\sqrt{2}+\sqrt{3})^2-5}}}$ = $\displaystyle {\frac{{6\sqrt{2}\cdot(\sqrt{2}+\sqrt{3}+\sqrt{5})}}{{2\sqrt{6}}}}$
	= $\displaystyle \sqrt{{3}}$ ^.( $\displaystyle \sqrt{{2}}$ + $\displaystyle \sqrt{{3}}$ + $\displaystyle \sqrt{{5}}$ ) = 3 + $\displaystyle \sqrt{{6}}$ + $\displaystyle \sqrt{{15}}$ .

Es soll also gelten:

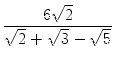a + $\displaystyle \sqrt{{b}}$ + $\displaystyle \sqrt{{c}}$ = $\displaystyle {\frac{{6\sqrt{2}}}{{\sqrt{2}+\sqrt{3}-\sqrt{5}}}}$ = 3 + $\displaystyle \sqrt{{6}}$ + $\displaystyle \sqrt{{15}}$ .

Nun kann man direkt ablesen, dass eine Lösung der Gleichung durch a = 3, b = 6 und c = 15 gegeben ist. Natürlich gibt es auch noch die Möglichkeit a = 3, b = 15 und c = 6 (aber keine weiteren, wie man mit einigem Aufwand zeigen kann).

Aufgabe 3

Die drei Musketiere Athos, Porthos und Aramis stehen wieder vor einer kniffligen Entscheidung: Wer muss am Abend den Abwasch erledigen?

Zur Entscheidungsfindung werfen sie diesmal jeder eine Münze so lange, bis sie zum ersten Mal ,,Zahl`` zeigt. Bei wem dies nach der geringsten Anzahl an Würfen geschieht, der muss abwaschen. Bei Gleichstand wird das Spiel wiederholt.

Mit welcher Wahrscheinlichkeit muss das Spiel wiederholt werden?

Lösung:

Sei p die Wahrscheinlichkeit dafür, dass das Spiel mit einem Gleichstand endet. Wir stellen uns vor, die drei werfen ihre Münzen immer zur gleichen Zeit. Ein solcher gemeinsamer Wurf hat dann genau 2³ = 8 mögliche Ergebnisse. In genau dreien davon, nämlich dann, wenn genau einer der drei ,,Zahl`` wirft, endet das Spiel. In genau einem Fall, nämlich wenn alle drei ,,Kopf`` werfen, kommt es zum nächsten gemeinsamen Wurf, und die Wahrscheinlichkeit, dass das Spiel im weiteren Verlauf zum Gleichstand führt, ist wieder p, da die folgenden Würfe unabhängig vom Vorherigen sind. In den restlichen vier Fällen herrscht zwischen mindestens zwei Spielern Gleichstand und das gesamte Spiel wird wiederholt.

Es ist also p = ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ p. Löst man dies nach p auf, so folgt p = ${\frac{{4}}{{7}}}$ .

Variante - Da man mit seinen ersten Überlegungen wahrscheinlich nicht gleich eine so elegante Lösung wie die eben vorgeführte findet, sei die Aufgabe hier auch noch mehr ,,zu Fuß`` vorgerechnet:

Im Folgenden nennen wir die Anzahl von getätigten Würfen einer Person, also die Nummer des Wurfes, bei dem erstmals ,,Zahl`` fällt, ,, Wurfzahl``.

Zunächst bemerken wir, dass das Spiel genau dann wiederholt wird, wenn entweder zwischen zwei Musketieren Gleichstand herrscht und der dritte eine höhere Wurfzahl als die anderen beiden hat oder wenn zwischen allen dreien Gleichstand herrscht. Nun definieren wir folgende Ereignisse:

A:: Es herrscht Gleichstand zwischen Athos und Porthos, und Aramis hat eine höhere Wurfzahl als die anderen beiden.
B:: Es herrscht Gleichstand zwischen Athos und Aramis, und Porthos hat eine höhere Wurfzahl als die anderen beiden.
C:: Es herrscht Gleichstand zwischen Porthos und Aramis, und Athos hat eine höhere Wurfzahl als die anderen beiden.
D:: Es herrscht Gleichstand zwischen Athos, Porthos und Aramis.

Seien weiterhin P(A), P(B), P(C) bzw. P(D) die Wahrscheinlichkeiten, dass A, B, C bzw. D eintritt. Dann sind A, B, C und D einander ausschließende Ereignisse, die zusammen alle Fälle einer Spielwiederholung darstellen. Somit folgt für die gesuchte Wahrscheinlichkeit P_ges = P(A) + P(B) + P(C) + P(D).

Wir betrachten nun das Ereignis A. Das Ereignis, dass ein Musketier n als Wurfzahl hat, also die Wurffolge (n - 1)-mal Kopf und dann einmal Zahl, besitzt die Wahrscheinlichkeit ( ${\frac{{1}}{{2}}}$ )^{n-1 .} ${\frac{{1}}{{2}}}$ = ( ${\frac{{1}}{{2}}}$ )ⁿ. Da eine Wurfzahl größer als n genau dem Fallen von Kopf in jedem der ersten n Würfe entspricht, ist die Wahrscheinlichkeit hierfür ebenfalls ( ${\frac{{1}}{{2}}}$ )ⁿ.

Somit beträgt die Wahrscheinlichkeit dafür, dass sowohl Athos als auch Porthos n als Wurfzahl und Aramis eine Wurfzahl größer n hat, ( ${\frac{{1}}{{2}}}$ )^{n .}( ${\frac{{1}}{{2}}}$ )^{n .}( ${\frac{{1}}{{2}}}$ )ⁿ = ( ${\frac{{1}}{{2}}}$ )³ⁿ = ( ${\frac{{1}}{{8}}}$ )ⁿ. Das Ereignis A bedeutet nun, dass dies für eine natürliche Zahl n eintritt. Somit ist P(A) = ( ${\frac{{1}}{{8}}}$ )¹ + ( ${\frac{{1}}{{8}}}$ )² + ( ${\frac{{1}}{{8}}}$ )³ +...= $\sum_{{n=1}}^{\infty}$ ( ${\frac{{1}}{{8}}}$ )ⁿ = ( $\sum_{{n=0}}^{\infty}$ ( ${\frac{{1}}{{8}}}$ )ⁿ) - 1 = ${\frac{{1}}{{1-\frac{1}{8}}}}$ - 1 = ${\frac{{8}}{{7}}}$ - 1 = ${\frac{{1}}{{7}}}$ (geometrische Reihe). Analog erhält man P(B) = P(C) = ${\frac{{1}}{{7}}}$ .

Nun berechnen wir noch P(D). Ähnlich wie oben beträgt die Wahrscheinlichkeit dafür, dass sowohl Athos als auch Porthos als auch Aramis die Wurfzahl n haben, ( ${\frac{{1}}{{2}}}$ )^{n .}( ${\frac{{1}}{{2}}}$ )^{n .}( ${\frac{{1}}{{2}}}$ )ⁿ = ( ${\frac{{1}}{{2}}}$ )³ⁿ = ( ${\frac{{1}}{{8}}}$ )ⁿ. Damit folgt wie oben P(D) = $\sum_{{n=1}}^{\infty}$ ( ${\frac{{1}}{{8}}}$ )ⁿ = ${\frac{{1}}{{7}}}$ . Als Gesamtergebnis ergibt sich somit

P_ges = P(A) + P(B) + P(C) + P(D) = $\displaystyle {\frac{{1}}{{7}}}$ + $\displaystyle {\frac{{1}}{{7}}}$ + $\displaystyle {\frac{{1}}{{7}}}$ + $\displaystyle {\frac{{1}}{{7}}}$ = $\displaystyle {\frac{{4}}{{7}}}$ .

Bemerkung: In dieser zweiten Lösung wird die Formel für die geometrische Reihe $\sum_{{n=0}}^{{\infty}}$ xⁿ = ${\frac{{1}}{{1-x}}}$ (mit x = ${\frac{1}{8}}$ ) benutzt. Indirekt steckt diese Formel auch in der ersten Variante in p = ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ p. Ersichtlich wird dies, wenn man auf der rechten Seite für p wieder p = ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ p einsetzt und rekursiv so fortfährt: p = ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ ( ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ p) = ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ ( ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ ( ${\frac{{4}}{{8}}}$ + ${\frac{{1}}{{8}}}$ (...))) = 4(( ${\frac{{1}}{{8}}}$ )¹ + ( ${\frac{{1}}{{8}}}$ )² + ( ${\frac{{1}}{{8}}}$ )³ +...).

Aufgabe 4

Die Zahlen von 1 bis 100 werden irgendwie zufällig auf die Felder eines 10×10-Spielbrettes verteilt.

Nun darf man in einem Zug beliebige zwei Zahlen auf dem Brett miteinander vertauschen. Ziel hierbei ist es, eine Konstellation zu erreichen, bei der die Summe keiner zwei horizontal, vertikal oder diagonal benachbarten Zahlen eine Primzahl ist.

Man beweise, dass man dies mit höchstens 38 Zügen erreichen kann.

Lösung:

Seien die Zahlen irgendwie zufällig verteilt. Dann gibt es unter den 50 Zahlen in den oberen fünf Zeilen des Brettes entweder höchstens 25 gerade oder höchstens 25 ungerade Zahlen (oder beides). Ohne Beschränkung der Allgemeinheit betrachten wir den ersten Fall; der zweite verläuft analog.

Es gibt also in der oberen Bretthälfte g $\leq$ 25 gerade Zahlen und entsprechend dann natürlich in der unteren Bretthälfte genau g ungerade Zahlen. Man kann daher durch paarweises Tauschen der geraden Zahlen in der oberen mit den ungeraden Zahlen in der unteren Hälfte in genau g Zügen erreichen, dass in den oberen fünf Zeilen nur ungerade und in den unteren fünf Zeilen nur gerade Zahlen stehen.

Nun betrachten wir die 20 Zahlen in den Zeilen 5 und 6. Sollte unter diesen die Zahl 1 sein, so nehmen wir diese aus der folgenden Betrachtung heraus. Es bleiben aber in jedem Fall noch mindestens 19 von 1 verschiedene Zahlen in den Zeilen 5 und 6.

Verteilt man diese Zahlen nun auf die drei Mengen

M_{0, 0}	= {Zahlen in Zeile 5, die bei Division durch 3 den Rest 0 lassen,
	und Zahlen in Zeile 6, die bei Division durch 3 den Rest 0 lassen},
M_{1, 2}	= {Zahlen in Zeile 5, die bei Division durch 3 den Rest 1 lassen,
	und Zahlen in Zeile 6, die bei Division durch 3 den Rest 2 lassen},
M_{2, 1}	= {Zahlen in Zeile 5, die bei Division durch 3 den Rest 2 lassen,
	und Zahlen in Zeile 6, die bei Division durch 3 den Rest 1 lassen},

so wird zum einen offenbar jede der mindestens 19 Zahlen genau einmal verteilt, zum anderen enthält eine der Mengen nach dem Schubfachprinzip dann mindestens 7 Zahlen. Sei dies die Menge M_{i, j}.

Da es sowohl unter den 50 ungeraden Zahlen in der oberen Hälfte des Brettes als auch unter den 50 geraden Zahlen in der unteren Hälfte des Brettes zu jedem der drei Divisionsreste bei Division durch 3 mehr als zehn Zahlen gibt, die eben jenen Rest bei Division durch 3 lassen, kann man nun - die gegebenenfalls vorhandene 1 wird wieder mit betrachtet - durch höchstens 20 - 7 = 13 weitere Vertauschungen innerhalb der oberen und innerhalb der unteren Hälfte erreichen, dass alle Zahlen in Zeile 5 den Rest i und alle Zahlen in Zeile 6 den Rest j bei Division durch 3 lassen und zusätzlich keine dieser Zahlen gleich 1 ist.

Insgesamt hat man damit nicht mehr als 25 + 13 = 38 Züge durchgeführt.

Die Summe zweier beliebiger (benachbarter) Zahlen in der oberen bzw. in der unteren Bretthälfte ist nun stets gerade und größer als 1 + 2 = 3, also, da gerade, mindestens gleich 4 und damit keine Primzahl.

Die Summe zweier benachbarter Zahlen entlang der ,,Grenze`` der beiden Hälften lässt nun bei Division durch 3 stets den Rest i + j. Nach Konstruktion der obigen drei Mengen ist aber i + j entweder gleich 0 oder 3; somit ist jede Summe benachbarter Zahlen entlang der Grenze durch 3 teilbar, und da keine dieser Zahlen gleich 1 ist, ist jede dieser Summen auch mindestens gleich 2 + 3 = 5, also, da durch 3 teilbar, mindestens gleich 6 und damit keine Primzahl.

Damit haben wir das Gewünschte in höchstens 38 Zügen erreicht.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File