Beispiellösungen zu Aufgabenblatt 71

aktualisiert: 8. Juli 2008

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.

Aufgabe 1

Carolin hat je ein Gewichtsstück der Masse 1 g, 2 g, 3 g, ..., 70 g. Kann sie diese so auf die beiden Seiten einer Balkenwaage verteilen, dass diese im Gleichgewicht ist?

Wie ist die Antwort, wenn sie unterm Bett noch ein Gewichtsstück der Masse 71 g findet und dieses mit verwenden will?

Lösung:

Im ersten Teil der Aufgabe berechnen wir die Summe aller Gewichtsstücke, also S₁ = 1g + 2g + + 70g = ${\frac{{70 \cdot 71}}{{2}}}$ g = 2485g. Dies ist eine ungerade Zahl, daher kann man die Gewichte nicht so auf zwei Waagschalen aufteilen, dass diese im Gleichgewicht sind.

Wenn wir beim zweiten Teil der Aufgabe die Summe der Gewichte ausrechnen, erhalten wir S₂ = 2485g + 71g = 2556g. Im Gegensatz zum ersten Teil ist dies eine gerade Zahl. Sie lässt sich als Produkt zerlegen in 2556 = 36^.71. Praktischerweise kann man die Gewichte vollständig zu Paaren zusammenfassen, die insgesamt je 71 g wiegen: 1g + 70g, 2g + 69g,..., 34g + 37g, 35g + 36g. Als einzige Ausnahme braucht das 71-g-Stück keinen Partner. (Nicht umsonst lässt hier übrigens der Beweis von Gauß für seine Summationsformel grüßen ...) Wir sehen, dass wir so 36 Teilmengen zu 71 g bilden können. Also legen wir auf jede Waagschale 18 dieser 71-g-Teilmengen und erhalten ein Gleichgewicht.

Bemerkung: Diese Anleitung liefert schon sehr viele Möglichkeiten, die Gewichte zu verteilen, es gibt aber immer noch andere Varianten.

Aufgabe 2

Drei Spielsteine stehen zu Beginn auf den Ecken eines gleichseitigen Dreiecks der Seitenlänge 1. In einem Zug darf einer der Steine an einem beliebigen anderen der Steine gespiegelt werden. Nach einer gewissen Anzahl an Zügen bilden die drei Steine wieder ein gleichseitiges Dreieck.

Welche Seitenlängen sind für dieses Dreieck möglich?

Lösung:

Wir betrachten zunächst ein allgemeines (nicht notwendigerweise gleichseitiges) Dreieck mit Eckpunkten A, B und C. Mit h_C bezeichnen wir die Höhe des Punktes C über der Seite AB, mit | AB| die Länge der Seite AB. Der Flächeninhalt F ist dann bekanntlich F = ${\frac{{1}}{{2}}}$ | AB|^.h_C.

Nun spiegeln wir einen der Eckpunkte an einem anderen Eckpunkt und erhalten ein Dreieck A'B'C'. Im Bild wird zunächst A an B gespiegelt (den Spiegelpunkt nennen wir A') und es gilt B' = B und C' = C. Wir sehen, dass | AB| = | A'B'| gilt, und auch die Höhe des Dreiecks hat sich durch das Spiegeln nicht verändert. Somit sind die Flächeninhalte der Dreiecke ABC und A'B'C' gleich.

Man sagt, der Flächeninhalt ist eine Invariante (konstante Größe) unter der Punktspiegelungsoperation.

Diese Tatsache gilt natürlich insbesondere für unser gleichseitiges Dreieck aus der Aufgabenstellung, d. h. ein durch mehrfaches Anwenden der Spiegelungsoperation erhaltenes gleichseitiges Dreieck muss denselben Flächeninhalt wie das Ausgangsdreieck haben. Also müssen auch die Seitenlängen dieselben sein.

Man kann sich noch leicht überlegen, dass man durch Anwenden der Spiegelungsoperation auch tatsächlich wieder zu einem gleichseitigen Dreieck kommen kann: Zum Beispiel durch Spiegeln von A an B und C' = C an B' = B. (In der Skizze oben entsteht durch dieses Vorgehen ebenfalls ein zum Ausgangsdreieck kongruentes Dreieck.)

Aufgabe 3

Unsere Piraten wollen sich auf Tortuga zur Ruhe setzen. Damit der Ruhestand möglichst angenehm wird, suchen sie noch ein letztes Mal Schätze im Wald der Insel. Von einem verstaubten Pergament vom Dachboden ihres Domizils wissen sie Folgendes:

Im - übrigens vollkommen ebenen - Wald gibt es bestimmte Bäume, in deren Rinde Abstandsdaten zu einem Schatz eingeritzt sind, und zwar jeweils der Abstand in x-, y- und z-Richtung; die z-Richtung beschreibt die Tiefe, in der der Schatz liegt. Die drei Zahlen sind allerdings in keiner bestimmten Reihenfolge angegeben.

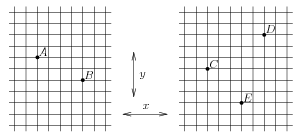
$\begin{picture}(0,0)% \includegraphics{schaetze.pstex}% \end{picture}$

picture(4524,2004)(529,-1513) (2656,-1141)(0,0)[lb] x% (2611,-646)(0,0)[lb] y% (1734,-669)(0,0)[lb] B% (3714,-489)(0,0)[lb] C% (4253,-1029)(0,0)[lb] E% (1014,-308)(0,0)[lb] A% (4609, 51)(0,0)[lb] D%

Zum ersten Schatz gibt es die Bäume A und B (siehe Skizze - sie haben also einen Abstand 4 in x-Richtung und 2 in y-Richtung) mit den Abstandswerten (0, 1, 2) und (1, 2, 4).

Die drei Bäume zum zweiten Schatz sind älter, bei ihnen kann man nicht mehr alle Zahlen lesen - bei C nur 4 und 4, bei D nur 6 und 7 und bei E nur eine 7.

Wo (und wie tief) liegen die Schätze?

Lösung:

Zunächst möchten wir einen allgemeinen Sachverhalt feststellen: Zwei Abstandswerte an zwei Bäumen können nur dann zur gleichen Koordinatenrichtung auf der Oberfläche (also x oder y) gehören, wenn entweder die Summe dieser beiden Werte gleich dem Abstand der beiden Bäume in der Koordinatenrichtung ist (dann liegt der Schatz in dieser Richtung zwischen den Bäumen) oder wenn die Differenz gleich deren Abstand ist - in diesem Fall liegt der Schatz jenseits des Baumes, der den kleineren Wert hat. (Sollte einer der beiden Werte null sein, treffen natürlich entweder beide Fälle zu oder sie treffen beide nicht zu.) In jedem Fall ist die Summe der beiden Abstände mindestens so groß wie der Abstand zwischen den Bäumen.

Ganz offensichtlich gilt für die z-Richtung, dass die Werte an beiden Bäumen gleich sein müssen.¹

Zu den Bäumen A und B betrachten wir besonders den Wert 4 bei Baum B. Er kann keine z-Koordinate sein, da der Wert 4 nicht auch bei A auftritt. Wäre er der y-Abstand zum Schatz - wir schreiben das als B_y = 4 -, so müsste A_y gleich 2 oder 6 sein, da der Abstand der Bäume in y-Richtung 2 ist. Es wäre also A_y = 2, weil es bei A keine 6 gibt. Dann gibt es jedoch keine Möglichkeit mehr, Werte für die x-Abstände zu finden, da die höchste noch erreichbare Summe von Abständen 1 + 2 = 3 beträgt.

Daher ist die 4 bei B der x-Abstand, B_x = 4. Es ist dann A_x = 0, da bei A keine 8 vorhanden ist. Nun kann keine y-Koordinate 2 sein, weil dann die Koordinate am anderen Baum 0 oder 4 sein müsste. Damit ist A_y = B_y = 1 und A_z = B_z = 2. Der Schatz liegt von A aus gesehen am Punkt (0, - 1) in der Tiefe 2.

Beim zweiten Fall betrachten wir als Erstes die Abstandsdaten an den Bäumen C und D. Da es nur drei Koordinatenrichtungen gibt, muss es (nach dem Schubfachprinzip) eine geben, die auf beiden noch zu lesenden Abstandspaaren vertreten ist. Weil D keine 4 hat, kann dies nicht die z-Richtung sein. Zur x-Richtung können auch nicht Werte auf beiden Bäumen gehören, weil sich 5 (der Abstand der Bäume in x-Richtung) weder als Differenz noch als Summe der gegebenen Werte darstellen lässt.

Damit steht auf jedem Baum der y-Abstand; und es bleibt wegen des Baumabstandes von 3 nur die Möglichkeit C_y = 4, D_y = 7, der Schatz liegt somit schon einmal 4 Einheiten südlich von C.

Die 7 bei E ist daher kein y-Abstand. Und da die Werte 4 bei C und 6 bei D nicht beides x-Abstände sein können, ist einer der Werte die Tiefe des Schatzverstecks und der andere ein x-Abstand. Damit kann die 7 bei E auch kein z-Abstand sein, es ist also E_x = 7. Wegen des Baumabstands 2 ist D_x $\neq$ 6, also muss 6 die Tiefe sein und zudem C_x = 4 gelten. Das passt auch zum x-Abstand 3 zwischen C und E, und damit liegt der Schatz je 4 Einheiten südlich und westlich von C in 6 Einheiten Tiefe.

$\begin{picture}(0,0)% \includegraphics{loes_schatz.pstex}% \end{picture}$

picture(5064,2004)(529,-1513) (2656,-1141)(0,0)[lb] x% (2611,-646)(0,0)[lb] y% (1734,-669)(0,0)[lb] B% (1014,-308)(0,0)[lb] A% (4254,-489)(0,0)[lb] C% (4793,-1029)(0,0)[lb] E% (5149, 51)(0,0)[lb] D%

Lösungsvariante: Mit etwas weniger Nachdenken, aber dafür etwas mehr (Schreib-)Arbeit kann man die Aufgabe auch mit einer Fallunterscheidung nach der möglichen Tiefe des Schatzes angehen. Wir wollen das nur skizzieren (und nur deshalb, so meinen wir, ist diese Lösung kürzer als die oben angegebene, ausführlich aufgeschriebene ...): Bei den Bäumen A und B muss die Tiefe 1 oder 2 sein; in beiden Fällen gibt es für jeden Baum für sich gesehen noch 8 Möglichkeiten, wo der Schatz liegen könnte; nur im Fall der Tiefe 2 sind darunter zwei gleiche Punkte.

Beim zweiten Schatz kann die Tiefe zum einen 4 sein; dann sind die Koordinaten bei D die Koordinaten auf der Oberfläche, also verbleiben noch 8 mögliche Orte. Keiner jedoch hat einen Abstand 7 in x- oder y-Richtung von Baum E.

Wenn die Tiefe nicht 4 ist, müssen die Koordinaten bei C die Oberflächenkoordinaten sein, womit es nur noch 4 mögliche Standorte gibt. Die Koordinate 6 von D kann dann keine x- oder y-Koordinate sein, weil sie zu keinem der vier Orte passt, damit ist die Tiefe 6, ferner ist (wie oben) die 7 bei D zwingend die y-Koordinate und schließlich die 7 bei E die x-Koordinate. Damit erhält man die Lösung.

Aufgabe 4

Gibt es positive, rationale Zahlen a und b, die beide nicht ganzzahlig sind, für die aber a + b und aⁿ + bⁿ ganzzahlig sind für

n = 2008?
n = 2009?

Lösung:

a) Seien a, b rationale, aber nicht-ganze Zahlen, welche die gegebenen Bedingungen erfüllen. Da a + b ganzzahlig ist, lassen sich beide Zahlen auf einen gemeinsamen Nenner q $\in$ $\mathbb {N}$ bringen, also als a = ${\frac{{p_1}}{{q}}}$ und b = ${\frac{{p_2}}{{q}}}$ schreiben, wobei p₁ und p₂ beide nicht durch q teilbar sind (denn sonst wäre a $\in$ $\mathbb {Z}$ oder b $\in$ $\mathbb {Z}$ ). Weiterhin folgt aus der Ganzzahligkeit der Summe a + b, dass p₁ + p₂ durch q teilbar ist, d. h. die Reste von a und b bei Division durch q addieren sich zu q. Somit gibt es einen Rest r mit 0 < r < q und ganze Zahlen n₁ und n₂ so, dass a = ${\frac{{n_1 \cdot q + r}}{{q}}}$ und b = ${\frac{{n_2 \cdot q -r}}{{q}}}$ gilt. Ohne Einschränkung können wir ggT(r, q)=1 annehmen (sonst könnten wir die Brüche kürzen).

Nun betrachten wir (unter Verwendung des Binomischen Lehrsatzes)

	a²⁰⁰⁸ + b²⁰⁰⁸ = 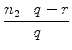$\displaystyle \left(\vphantom{\frac{n_1 \cdot q + r}{q}}\right.$ $\displaystyle {\frac{{n_1 \cdot q + r}}{{q}}}$ $\displaystyle \left.\vphantom{\frac{n_1 \cdot q + r}{q}}\right)^{{2008}}_{}$ + $\displaystyle \left(\vphantom{\frac{n_2 \cdot q - r}{q}}\right.$ $\displaystyle {\frac{{n_2 \cdot q - r}}{{q}}}$ $\displaystyle \left.\vphantom{\frac{n_2 \cdot q - r}{q}}\right)^{{2008}}_{}$
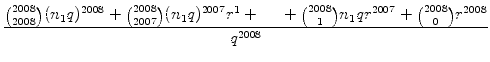	= $\displaystyle {\frac{{ \binom{2008}{2008} (n_1q)^{2008} + \binom{2008}{2007} (n... ...dots + \binom{2008}{1} n_1 q r^{2007} + \binom{2008}{0} r^{2008}}}{{q^{2008}}}}$
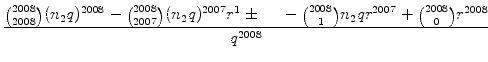	+ $\displaystyle {\frac{{\binom{2008}{2008} (n_2q)^{2008} - \binom{2008}{2007} (n_... ...ldots - \binom{2008}{1} n_2 q r^{2007} + \binom{2008}{0}r^{2008}}}{{q^{2008}}}}$ .

Im Fall q > 2 sind alle Summanden des Zählers bis auf r²⁰⁰⁸ + r²⁰⁰⁸ = 2^.r²⁰⁰⁸ durch q teilbar. Da 2^.r²⁰⁰⁸ jedoch nach Voraussetzung zu q teilerfremd ist, ist der gesamte Zähler nicht durch q und damit auch nicht durch q²⁰⁰⁸ teilbar. Somit ist in diesem Fall a²⁰⁰⁸ + b²⁰⁰⁸ keine ganze Zahl.

Im Fall q = 2 muss r = 1 sein. Daher ist 2^.r²⁰⁰⁸ = 2 nicht durch q² = 4 teilbar. Da alle anderen Summanden des Zählers jedoch entweder den Faktor q² oder $\binom{2008}{1}$ ^.q = 4016 = 4^.1004 enthalten, werden diese von q² geteilt. Somit ist der Zähler auch nicht durch q²⁰⁰⁸ = (q²)¹⁰⁰⁴ teilbar, das heißt, auch hier ist a²⁰⁰⁸ + b²⁰⁰⁸ keine ganze Zahl.

Somit gibt es kein Zahlenpaar (a, b), das die Bedingungen erfüllt.

b) Eine analoge Überlegung wie im ersten Teil kann man selbstverständlich auch hier anstellen. Der Unterschied ist, dass die Vorzeichen der jeweils letzten Terme im Zähler verschieden sind - damit fallen sie in der Gesamtsumme weg. Nun haben aber alle verbleibenden Summanden im Zähler mindestens einen Faktor n_i und einen Faktor q. Wenn man dafür sorgt, dass jedes n_i durch q²⁰⁰⁸ teilbar ist, ist jeder Summand durch q²⁰⁰⁹ teilbar und man erhält quasi automatisch eine ganze Zahl.

Damit findet man sehr schnell ein Beispiel, was wir dennoch vollständig durchrechnen wollen (wir wählen q = 2, n₁ = 0, n₂ = 2²⁰⁰⁸ und r = 1):

Es seien a = ${\frac{{1}}{{2}}}$ und b = ${\frac{{2^{2009}-1}}{{2}}}$ . Dann sind a und b rational, aber nicht ganzzahlig. Weiterhin ist a + b = ${\frac{{2^{2009}}}{{2}}}$ = 2²⁰⁰⁸ ganzzahlig und es gilt:

	a²⁰⁰⁹ + b²⁰⁰⁹
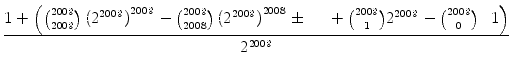	= $\displaystyle {\frac{{1 + \left(\binom{2009}{2009} \left(2^{2009}\right)^{2009}... ...\ldots + \binom{2009}{1} 2^{2009} -\binom{2009}{0}\cdot 1\right)}}{{2^{2009}}}}$
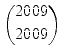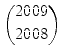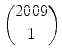	= $\displaystyle \binom{2009}{2009}$ $\displaystyle \left(\vphantom{2^{2009}}\right.$ 2²⁰⁰⁹ $\displaystyle \left.\vphantom{2^{2009}}\right)^{{2008}}_{}$ - $\displaystyle \binom{2009}{2008}$ $\displaystyle \left(\vphantom{2^{2009}}\right.$ 2²⁰⁰⁹ $\displaystyle \left.\vphantom{2^{2009}}\right)^{{2007}}_{}$ ±...+ $\displaystyle \binom{2009}{1}$

ist eine ganze Zahl. Also erfüllen a und b die Bedingungen.

Fußnoten

... m"ussen.¹: Genaugenommen ist das auch nur ein Spezialfall der vorigen Betrachtung, nämlich der Fall, dass der Abstand der Bäume in einer Koordinatenrichtung null ist.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File