Beispiellösungen zu Aufgabenblatt 72

aktualisiert: 12. September 2008

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.

Aufgabe 1

Die folgende ,,falsche`` Kürzung eines Bruches führt zufälligerweise zu einem richtigen Ergebnis:

$\displaystyle {\frac{{16}}{{64}}}$ = $\displaystyle {\frac{{1\!\!\!\not{\hspace{-0.4mm}6}}}{{\!\not{\hspace{-0.4mm}6}4}}}$ = $\displaystyle {\textstyle\frac{1}{4}}$ .

Finde alle Brüche mit zweistelligem Zähler und Nenner, die auf die gleiche (falsche) Weise zu einer richtigen Kürzung führen.

Lösung:

Wie in der Aufgabenstellung vorgegeben wollen wir Brüche mit je zweistelligem Zähler und Nenner betrachten, wobei Einerstelle des Zählers und Zehnerstelle des Nenners identisch seien, also Brüche der Form ${\frac{{10a+b}}{{10b+c}}}$ .

Da sowohl 10a + b als auch 10b + c zweistellig sein sollen, muss a, b $\in$ {1,..., 9} gelten. Weiterhin wollen wir ,,falsch`` kürzen, d. h. wir wollen den gegebenen Term mit dem Bruch ${\frac{{a}}{{c}}}$ vergleichen. Daher muss c $\neq$ 0 gelten, also auch c $\in$ {1,..., 9}.

Das ,,falsche`` Kürzen funktioniert unter diesen Voraussetzungen genau dann, wenn

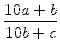	$\displaystyle {\frac{{10a+b}}{{10b+c}}}$	= $\displaystyle {\frac{{a}}{{c}}}$
$\displaystyle \Leftrightarrow$	10ac + bc	= 10ab + ac
$\displaystyle \Leftrightarrow$	9ac	= b^.(10a - c)	(1)

Aus Gleichung () folgt, dass 9 den Term b^.(10a - c) teilt. Wir unterscheiden zwei Fälle:

1. Fall: 9 teilt 10a - c.
Es gilt 10a - c = 9a + (a - c) und 9| 9a, und somit ist dieser Fall äquivalent zu 9|(a - c). Wegen a, c $\in$ {1,..., 9} ist weiterhin -9 = 0 - 9 < a - c < 9 - 0 = 9, und zusammen mit 9|(a - c) ergibt sich a - c = 0 oder äquivalent a = c.

Setzen wir dies in () ein, erhalten wir: 9a² = 9ab, also a = b = c.

Probe: Es ist ${\frac{{10a +a}}{{10a + a}}}$ = 1 = ${\frac{{a}}{{a}}}$ für alle a $\in$ {1,..., 9}.

2. Fall: 3 teilt b.
Fall 2a: b = 3.
In diesem Fall erhalten wir aus (), dass 3ac = 10a - c gelten muss, also c = ${\frac{{10a}}{{3a+1}}}$ . Da c insbesondere ganzzahlig ist, folgt daraus (3a + 1)| 10a und mit 10a = 3^.(3a + 1) + a - 3 schließlich (3a + 1)|(a - 3). Da 3a + 1 $\geq$ 4 und 3a + 1 > a - 3 $\geq$ - 2 gelten, kann dies nur im Fall a - 3 = 0, d. h. a = 3 erfüllt sein. Dies liefert c = ${\frac{{10\cdot 3}}{{3\cdot 3+1}}}$ = 3. Wir haben also einen Spezialfall der Lösung aus dem 1. Fall mit a = b = c = 3.

Fall 2b: b = 6.
Gleichung () liefert uns nun 3ac = 20a - 2c, also c = ${\frac{{20a}}{{3a+2}}}$ , woraus wie oben (3a + 2)| 20a folgt. Dieses ist nur für a $\in$ {1, 2, 6} erfüllt. Mit c = ${\frac{{20a}}{{3a+2}}}$ erhalten wir für c entsprechend die Werte 4, 5 und 6.

Probe: ${\frac{{16}}{{64}}}$ = ${\frac{{1}}{{4}}}$ , ${\frac{{26}}{{65}}}$ = ${\frac{{2}}{{5}}}$ sowie wie im 1. Fall ${\frac{{66}}{{66}}}$ = 1 = ${\frac{{6}}{{6}}}$ .

Fall 2c: b = 9
Hier gilt aufgrund von (), dass ac = 10a - c und somit c = ${\frac{{10a}}{{a+1}}}$ ist. Aus der Ganzzahligkeit von c erhalten wir (a + 1)| 10a und mit 10a = 10(a + 1) - 10, dass (a + 1)| 10 gilt. Also ist a + 1 $\in$ {1, 2, 5, 10} bzw. a $\in$ {1, 4, 9}. Die Gleichung c = ${\frac{{10a}}{{a+1}}}$ liefert uns für c entsprechend 5, 8 und 9.

Probe: ${\frac{{19}}{{95}}}$ = ${\frac{{1}}{{5}}}$ , ${\frac{{49}}{{98}}}$ = ${\frac{{1}}{{2}}}$ = ${\frac{{4}}{{8}}}$ sowie wie im 1. Fall ${\frac{{99}}{{99}}}$ = 1 = ${\frac{{9}}{{9}}}$ .

Insgesamt haben wir also folgende Lösungen gefunden: ${\frac{{\overline{aa}}}{{\overline{aa}}}}$ mit a $\in$ {1,..., 9}, ${\frac{{16}}{{64}}}$ , ${\frac{{26}}{{65}}}$ , ${\frac{{19}}{{95}}}$ und ${\frac{{49}}{{98}}}$ . Aus der obigen Fallunterscheidung geht hervor, dass dies alle Lösungen sind.

Bemerkung zur Notation: Wir verwenden die Notation $\overline{{xy}}$ als Schreibweise für die Zifferndarstellung, also $\overline{{xy}}$ : = 10x + y.

Lösungsvariante

Diese Aufgabe ist ein Beispiel dafür, dass anderes Umstellen zwar zu einer Lösung mit im Prinzip gleicher Argumentation, aber tatsächlich anderen verwendeten Zahlenwerten führt:

Wie oben folgern wir, dass a, b und c Elemente von {1,..., 9} sind.

Wir stellen noch einmal die Ausgangsgleichung um:

Das ,,falsche`` Kürzen funktioniert genau dann, wenn

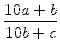	$\displaystyle {\frac{{10a+b}}{{10b+c}}}$	= $\displaystyle {\frac{{a}}{{c}}}$
$\displaystyle \Leftrightarrow$	10ac + bc	= 10ab + ac
$\displaystyle \Leftrightarrow$	c^.(b - a)	= 10^.a^.(b - c)	(2)

Zusätzlich gilt dann:

10b + c = $\displaystyle {\frac{c}{a}}$ (10a + b) = 10c + $\displaystyle {\frac{c}{a}}$ b.

Wäre c > b, müsste 10b + c < 10(b + 1) $\leq$ 10c < 10c + ${\frac{c}{a}}$ b = 10b + c sein (wegen c $\leq$ 9 und ${\frac{c}{a}}$ b > 0), dies ist ein Widerspruch. Also folgt

c $\displaystyle \leq$ b.

Damit ist die rechte Seite in () nichtnegativ; also muss auch b - a $\geq$ 0 gelten.

Nun stehen auf beiden Seiten in () ganze Zahlen, daher ist 10 und damit auch 5 ein Teiler von c^.(b - a). Wegen 0 $\leq$ c $\leq$ 9 und 0 $\leq$ b - a $\leq$ 9 gilt c = 5 oder 5|(b - a).

1. Fall: c = 5.
Dann kann wegen c $\leq$ b die Zahl b nur in der Menge {5, 6,..., 9} liegen. Aus () ergibt sich durch Umstellen

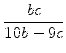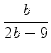a = $\displaystyle {\frac{{bc}}{{10b - 9c}}}$ = $\displaystyle {\frac{{b}}{{2b - 9}}}$ .

Wir machen eine Tabelle mit den verbleibenden Möglichkeiten; wenn sich für a kein ganzzahliger Wert ergibt, kann sich daraus keine Lösung ergeben.

b	a	Probe
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 5	5	$\displaystyle {\frac{{55}}{{55}}}$ = $\displaystyle {\textstyle\frac{5}{5}}$
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 6	2	$\displaystyle {\frac{{26}}{{65}}}$ = $\displaystyle {\textstyle\frac{2}{5}}$
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 7	$\displaystyle {\frac{{7}}{{5}}}$	-
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 8	$\displaystyle {\frac{{8}}{{7}}}$	-
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 9	1	$\displaystyle {\frac{{19}}{{95}}}$ = $\displaystyle {\textstyle\frac{1}{5}}$

2. Fall: 5|(b - a).
Fall 2a: b = a.
Dieser Fall ist einfach: Aus () folgt sofort b = c = a und damit ergeben sich die trivialen Lösungen ${\frac{{\overline{aa}}}{{\overline{aa}}}}$ = ${\frac{a}{a}}$ mit a $\in$ {1, 2,..., 9}.

Fall 2a: b $\neq$ a.
Auch hier machen wir eine Tabelle mit den verbleibenden Möglichkeiten. Man beachte dabei, dass sich aus der Wahl von b der Wert von a eindeutig aus der Bedingung 5|(b - a) und a > 0 ergibt: Da außerdem wie oben gezeigt b $\geq$ a gilt, muss b $\geq$ 6 und a = b - 5 sein.

Der Wert von c ergibt sich hier aus der Umstellung c = ${\frac{{10ab}}{{10a + b-a}}}$ = ${\frac{{10 ab}}{{10a + 5}}}$ = ${\frac{{2ab}}{{2a+1}}}$ der Gleichung ().

b	a	c	Probe
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 6	1	4	$\displaystyle {\frac{{16}}{{64}}}$ = $\displaystyle {\textstyle\frac{1}{4}}$
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 7	2	$\displaystyle {\frac{{28}}{{5}}}$	-
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 8	3	$\displaystyle {\frac{{48}}{{7}}}$	-
$\displaystyle \raisebox{-1.0ex}{\rule{0mm}{3.2ex}}$ 9	4	8	$\displaystyle {\frac{{49}}{{98}}}$ = $\displaystyle {\textstyle\frac{4}{8}}$

Es ergeben sich also dieselben Lösungen wie oben: ${\frac{{16}}{{64}}}$ , ${\frac{{26}}{{65}}}$ , ${\frac{{19}}{{95}}}$ und ${\frac{{49}}{{98}}}$ sowie ${\frac{{\overline{aa}}}{{\overline{aa}}}}$ mit a $\in$ {1,..., 9}.

Anmerkung:

Wir meinten mit unserer Aufgabenstellung, dass diagonal ,,links unten gegen rechts oben`` gekürzt wird.

Für den Fall, dass man allgemeiner andere gleiche Ziffern wegkürzen will, wollen wir das auch kurz behandeln:

Fall 1: Diagonales Kürzen andersherum

Es soll also ${\frac{{\overline{ab}}}{{\overline{ca}}}}$ = ${\frac{b}{c}}$ sein. Dieser Fall ist äquivalent zu dem oben behandelten: Man bilde einfach die Kehrwerte.

Fall 2: Senkrechtes Kürzen in den Zehnerstellen

Hier führt der Ansatz ${\frac{{\overline{ab}}}{{\overline{ac}}}}$ = ${\frac{b}{c}}$ sofort zu der Gleichheit 10ac + bc = 10ab + bc, weiter 10ac = 10ab, damit b = c und nach Einsetzen zu ${\frac{{\overline{ab}}}{{\overline{ab}}}}$ = ${\frac{b}{b}}$ = 1 mit a, b $\in$ {1, 2,..., 9}; es gibt also im Prinzip nur ,,triviale`` Fälle.

Fall 3: Senkrechtes Kürzen in den Einerstellen

Hier führt der Ansatz ${\frac{{\overline{ab}}}{{\overline{cb}}}}$ = ${\frac{a}{c}}$ unmittelbar zu der Gleichheit 10ac + bc = 10ac + ab. Es ist dann entweder b = 0 oder es folgt weiter bc = ab, damit a = c und nach Einsetzen ${\frac{{\overline{ab}}}{{\overline{ab}}}}$ = ${\frac{a}{a}}$ = 1 mit a, b $\in$ {1, 2,..., 9}; auch hier gibt es daher im Prinzip nur ,,triviale`` Fälle.

Aufgabe 2

Theo hat zwei Würfel, auf denen jeweils wie üblich die Zahlen von 1 bis 6 je genau einmal verteilt sind. Susi hingegen hat zwei Würfel, von denen man nur weiß, dass auf jeder ihrer Seitenflächen eine positive ganze Zahl steht. Hierbei müssen Susis Würfel nicht unbedingt beide gleich beschriftet sein und es dürfen auch Zahlen mehrfach auf einem Würfel vorkommen.

Nun stellt sich heraus: Für jede der Zahlen n = 2, 3, 4,..., 12 ist die Wahrscheinlichkeit, dass Theo mit seinen Würfeln die Augensumme n wirft, genauso groß wie die Wahrscheinlichkeit, dass Susi diese Augensumme wirft.

Muss Susi auch jeweils die Zahlen von 1 bis 6 auf jedem ihrer Würfel haben?

Lösung:

Bei einem herkömmlichen Würfelpaar hat man folgende Wahrscheinlichkeiten für die Augensummen n = 2, 3, 4,..., 12:

Augensumme	2	3	4	5	6	7	8	9	10	11	12
Möglichkeiten	1	2	3	4	5	6	5	4	3	2	1
Wahrscheinlichkeit	${\frac{{1}}{{36}}}$	${\frac{{2}}{{36}}}$	${\frac{{3}}{{36}}}$	${\frac{{4}}{{36}}}$	${\frac{{5}}{{36}}}$	${\frac{{6}}{{36}}}$	${\frac{{5}}{{36}}}$	${\frac{{4}}{{36}}}$	${\frac{{3}}{{36}}}$	${\frac{{2}}{{36}}}$	${\frac{{1}}{{36}}}$

Aus der Tatsache, dass Susis Würfelpaar für jede Augensumme dieselbe Wahrscheinlichkeit haben soll, folgt - da auch sie zwei Würfel und damit genau 36 verschiedene Möglichkeiten hat -, dass es für jede Augensumme bei Susi dieselbe Anzahl von Möglichkeiten gibt. Mit diesem Hauptargument wollen wir nun die Lösung ableiten.

Leicht sieht man, dass jeder von Susis Würfeln genau eine Eins haben muss, da es sonst keine oder mehr Kombinationsmöglichkeiten gäbe, eine Zwei zu würfeln.

Es folgt nun eine etwas umfangreiche Fallunterscheidung; zur besseren Mitverfolgbarkeit ist bei jedem Unterfall auch noch in einer kleinen Tabelle der aktuelle Stand der Belegung der Würfel angegeben:

1	.	.	.	.	.
1	.	.	.	.	.

Susi hat nach Voraussetzung genau zwei Möglichkeiten, eine Drei zu würfeln. Daher müssen auf den beiden Würfeln insgesamt genau zwei Zweien vorhanden sein, denn auf jedem Würfel kann sich eine Zwei mit der genau einen Eins auf dem anderen Würfel zu einer Drei addieren.

Fall 1: Jeder Würfel von Susi hat genau eine Zwei.

1	2	.	.	.	.
1	2	.	.	.	.

Die Würfel müssen zusammen zwei Dreien besitzen, da wir sonst für die Augensumme vier nicht genau drei Möglichkeiten hätten (möglich sind (1, 3), (3, 1), (2, 2)).

Für die Verteilung der Dreien gibt es wieder zwei Variationen.

Fall 1.1: Ein Würfel hat beide Dreien.

1	2	3	3	.	.
1	2	.	.	.	.

Für die Augensumme fünf gibt es bislang bereits zwei Möglichkeiten. Auf den zweiten Würfel darf keine Drei kommen, weil es dann zu viele Möglichkeiten für eine Vier gäbe. Also müssen Vieren für die fehlenden Möglichkeiten sorgen; wir brauchen davon mit dem gleichen Argument wie oben genau zwei Stück.

1	2	3	3	4	4
1	2	.	.	.	.

1	2	3	3	4	.
1	2	4	.	.	.

1	2	3	3	.	.
1	2	4	4	.	.

In jedem Fall gibt es bislang zwei Möglichkeiten für die Augensumme sechs. Also muss es insgesamt genau drei Fünfen geben, um auf fünf Möglichkeiten zu kommen.

Beim ersten der drei Muster sind es dann schon sechs Möglichkeiten für eine Acht - zu viele!

Wenn beim zweiten Muster die drei Fünfen zum unteren Würfel kommen, gilt das gleiche Argument.

Wenn dort eine Fünf auf den ersten Würfel kommt, muss die letzte Ziffer auf dem zweiten Würfel eine Sieben sein, damit auch die Zwölf darstellbar ist. Dann jedoch gibt es nur eine Möglichkeit für eine Elf - Widerspruch!

Beim letzten Muster muss ebenso die letzte zu verteilende Ziffer eine Sieben sein. Dann gibt es jedoch bereits zwei Möglichkeiten für die Zwölf, so dass dies auch nicht geht.

Fall 1.2: Jeder Würfel hat genau eine Drei.

1	2	3	.	.	.
1	2	3	.	.	.

Es wiederholt sich im Folgenden immer wieder ein ähnliches Argumentationsmuster: Neue Ziffern müssen größer als die bereits vergebenen sein, da sonst bereits fertig untersuchte Summen mehr Möglichkeiten erhalten würden. Die Anzahl der zu verteilenden Ziffern ist gleich der Anzahl der noch fehlenden Möglichkeiten, da sie für die gerade untersuchte Summe mit der jeweils nur einmal vorhandenen Eins summiert werden müssen.

Hier gibt es also für die Summe fünf noch zwei Vieren zu verteilen.

Zunächst nehmen wir an, dass beide Vieren auf einem Würfel sind.

1	2	3	4	4	.
1	2	3	.	.	.

Dann müssten wir noch zwei Fünfen für die Augensumme sechs verteilen. Diese, so nehmen wir an, seien zusammen auf dem zweiten Würfel.

1	2	3	4	4	.
1	2	3	5	5	.

Dann gäbe es für die letzten beiden freien Plätze nur noch zwei Sechsen, damit wir nur einmal eine Zwölf würfeln können. Dies ist aber ein Widerspruch, da wir dann für die Augensumme zehn nur zwei Möglichkeiten hätten statt drei.

Wenn jeder Würfel genau eine der beiden Fünfen hat,

1	2	3	4	4	5
1	2	3	5	.	.

dann muss der zweite Würfel genau eine Sieben haben, damit die Augensumme 12 genau eine Wurfmöglichkeit besitzt. Der letzte freie Platz müsste dann allerdings von einer Sechs ausgefüllt werden. Damit gäbe es aber vier statt drei Möglichkeiten, eine Zehn zu würfeln.

Das bedeutet: Jeder Würfel besitzt (im Fall 1) auch genau eine Vier.

1	2	3	4	.	.
1	2	3	4	.	.

Wir brauchen nun allerdings noch zwei Fünfen, um fünf Möglichkeiten zu erhalten, eine Sechs zu würfeln. Diese können nicht auf demselben Würfel liegen, da dann auf dem anderen eine Sieben sein müsste, damit wir noch die Augensumme 12 würfeln können. Für diese gäbe es dann allerdings gleich zwei Möglichkeiten.

Also hat auch jeder Würfel genau eine Fünf und die letzten beiden Augenzahlen müssen dann Sechsen sein. Damit hat Susi im Fall 1 ebenfalls zwei normale Würfel.

Fall 2: Ein Würfel besitzt genau zwei Zweien und der andere keine.

1	2	2	.	.	.
1	.	.	.	.	.

Die beiden Würfel müssen dann noch zusammen drei Dreien enthalten, damit wir für die Augensumme vier drei Möglichkeiten haben. Diese können auf vier verschiedene Weisen verteilt sein. Der Würfel mit den Zweien (Würfel A) könnte alle drei Dreien, zwei, eine oder keine Drei enthalten.

Fall 2.1: A enthält alle drei Dreien.

1	2	2	3	3	3
1	.	.	.	.	.

Für die Augensumme zwölf muss der zweite Würfel dann eine Neun enthalten, was jedoch zu mindestens drei Möglichkeiten (anstatt einer) führt, eine Zwölf zu würfeln.

Fall 2.2: A enthält keine Drei.

1	2	2	.	.	.
1	3	3	3	.	.

Dann sind alle Dreien auf dem anderen Würfel und es gibt bereits sechs statt vier Möglichkeiten, eine Fünf zu würfeln.

Fall 2.3: A enthält genau eine Drei:

1	2	2	3	.	.
1	3	3	.	.	.

Dann gibt es schon vier Möglichkeiten für die Summe Fünf. Also hat keiner der Würfel eine Vier, da es dann mehr als vier Möglichkeiten gäbe, eine Fünf zu würfeln.

Die Würfel müssten dann allerdings noch drei Fünfen enthalten, da wir auch fünf Möglichkeiten brauchen, eine Sechs zu würfeln.

Nun haben wir drei Unterfälle zu betrachten:

Fall 2.3.1: A hat keine Fünf.

1	2	2	3	.	.
1	3	3	5	5	5

Hier muss der zweite Würfel für die Augensumme zwölf eine Sieben haben, was aber wiederum zu mindestens drei Möglichkeiten (anstatt einer) führt, diese Summe zu würfeln.

Fall 2.3.2: A hat genau eine Fünf.

1	2	2	3	5	.
1	3	3	5	5	.

Um sechs Möglichkeiten für die Augensumme Sieben zu erhalten, müssten dann die beiden verbleibenden Plätze jeweils eine Sechs haben. Damit hätte man jedoch drei statt zwei Möglichkeiten für die Augensumme elf.

Fall 2.3.3: A hat zwei Fünfen.

1	2	2	3	5	5
1	3	3	5	.	.

Dann muss der zweite Würfel für die Augensumme zwölf eine Sieben enthalten, was zu mindestens zwei Möglichkeiten (anstatt einer) führt, diese Summe zu würfeln.

Fall 2.4: Damit bleibt nur noch: Würfel A hat zwei Dreien.

1	2	2	3	3	.
1	3	.	.	.	.

Wir brauchen dann noch zwei Vieren, damit wir für die Augensumme fünf vier Kombinationen haben.

Fall 2.4.1: A hat keine Vier.

1	2	2	3	3	.
1	3	4	4	.	.

Damit haben wir bereits mindestens sechs (statt fünf) Möglichkeiten für die Augensumme sechs.

Es bleibt Fall 2.4.2: A hat genau eine Vier.

1	2	2	3	3	4
1	3	4	.	.	.

In diesem Fall müssen wir für die Augensumme sechs noch eine Fünf hinzufügen. Für die sechs Möglichkeiten der Summe sieben müssen wir noch eine Sechs ergänzen und für die Augensumme neun noch eine Acht.

Auch für die restlichen Augensummen stimmt die Anzahl der Kombinationen mit der eines normalen Würfelpaares überein. Damit könnte Susi also auch die beiden Würfel 1, 2, 2, 3, 3, 4 und 1, 3, 4, 5, 6, 8 haben.

Skizze einer alternativen Lösung:

Mit Hilfe sogenannter ,,erzeugender Funktionen`` kann man auch folgendermaßen zu einer Lösung kommen.

Für jede der Zahlen n = 1, 2, 3,,... seien e_n bzw. z_n die Anzahlen der Zahlen n, die auf dem ersten bzw. zweiten Würfel vorkommen. Da nur sechs Zahlen auf jedem Würfel stehen, sind insbesondere bei allen denkbaren Würfeln fast alle e_n bzw. z_n gleich null (höchstens sechs sind von null verschieden).

Man definiert sich zwei (Polynom-)Funktionen E(x) = e₁x¹ + e₂x² +... und Z(x) = z₁x¹ + z₂x² +... Jetzt kommt der Trick: Berechnet man nämlich nun das Produkt E(x)^.Z(x) = (e₁z₁)x² + (e₁z₂ + e₂z₁)x³ +..., so ist der Koeffizient vor x^m im Produkt gerade die Anzahl der Möglichkeiten, wie man den Exponenten m als Summe aus einem der in E vorkommenden Exponenten von x und einem der in Z vorkommenden Exponenten darstellen kann, wobei die Exponenten in E bzw. Z entsprechend ihrer Vielfachheit, die durch die e_n bzw. z_n gegeben sind, gezählt werden.

Für zwei Standardwürfel gilt also

E(x) = Z(x) = x + x² + x³ + x⁴ + x⁵ + x⁶

und somit

E(x)^.Z(x) = x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹².

Zur Überprüfung: Es gibt also zum Beispiel 5 Möglichkeiten, mit zwei Standardwürfeln die Summe 8 zu würfeln, denn der Koeffizient vor x⁸ im Produkt ist 5.

Die Frage ist nun: Gibt es zwei andere von Würfelbeschriftungen stammende Polynome E(x) und Z(x), für die E(x)^.Z(x) = x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹² ist?

Um dies zu beantworten, kann man zunächst das Produkt vollständig in Faktoren zerlegen - und diese Zerlegung ist eindeutig, was wir hier nicht beweisen wollen:

x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹²	=
x²(x + 1)²(x² - x + 1)²(x² + x + 1)²	.

Man kann nun versuchen, diese acht Faktoren unter gewissen Nebenbedingungen zu zwei Polynomen zu kombinieren: Zunächst muss sowohl E(x) als auch Z(x) einen Faktor x bekommen, denn andernfalls hätte ein Würfel eine 0 auf einer seiner Seiten (die erzeugende Funktion des Würfels hätte einen Summanden x⁰ = 1) , was nicht sein soll. Weiter muss die Summe aller Koeffizienten in E(x) und Z(x) genau 6 sein, damit man genau sechs Zahlen auf die Seiten verteilt. Da die Summe der Koeffizienten in E(x) und Z(x) gerade der Wert E(1) bzw. Z(1) ist, muss man also obige Faktoren an der Stelle 1 auswerten (das ergibt der Reihe nach die Werte 1 für x, 2 für x + 1, 1 für x² - x + 1 und 3 für x² + x + 1) und diese Werte dann zu zwei Produkten mit Wert 6 kombinieren. Demnach muss sowohl E(x) als auch Z(x) je einmal den Faktor x + 1 und x² + x + 1 enthalten. Einzig die Verteilung der beiden letzten Faktoren x² - x + 1 ist zunächst frei.

Es bleiben also die beiden Möglichkeiten

E(x)	= x(x + 1)(x² + x + 1)(x² - x + 1) = x + x² + x³ + x⁴ + x⁵ + x⁶
	und
Z(x)	= E(x)

und

E(x)	= x(x + 1)(x² + x + 1)(x² - x + 1)²
	= x + x³ + x⁴ + x⁵ + x⁶ + x⁸
	und
Z(x)	= x(x + 1)(x² + x + 1) = x + 2x² + 2x³ + x⁴.

Die erste Möglichkeit entpricht der zweier Standardwürfel, die zweite liefert eine Beschriftung von 1, 3, 4, 5, 6, 8 für den ersten und 1, 2, 2, 3, 3, 4 für den zweiten Würfel.

Die Probe bestätigt, dass diese beiden Paare alle Bedingungen erfüllen.

Aufgabe 3

Die Bundeskanzlerin empfängt an einer langen Tafel Staatsgäste, und zwar zwei aus Triangulanien und drei aus Zirkulanien. Diese sollen alle an einer der langen Seiten eines rechteckigen Tisches sitzen und jeder Gast bekommt ein Platzdeckchen, welches sich mit keinem anderen Deckchen überlappt, nicht über den Rand des Tisches hinausragt, aber in jedem Fall die Seite des Tisches, an der die Gäste sitzen, in wenigstens einem Punkt berührt.

Die Zirkulanier essen bekanntlich nur von kreisförmigen Deckchen mit Durchmesser 1 Meter und die Triangulanier würden das Essen nicht anrühren, wenn ihre Deckchen nicht die Form gleichseitiger Dreiecke mit Höhe 1 Meter hätten.

Finde die Länge eines möglichst kurzen Tisches, der ein zufriedenes Essen garantiert.

Lösung:

Die drei kreisförmigen Deckchen können nur so liegen, dass sie den Tischrand genau berühren. Mit ihnen muss der Tisch schon einmal mindestens drei Meter lang sein.

Die Frage ist also, wie die zwei dreieckigen Deckchen zu den runden hinzugefügt werden sollen.

Wir berechnen dazu zunächst grundsätzlich den horizontalen Abstand der Mittelpunkte eines Dreiecks und eines Kreises, wenn sie sich wie folgt berühren:

$\includegraphics[]{l31}$

b sei der Radius des Kreises, der senkrecht auf der Tischkante steht. a sei der Radius, der dazu in einem Winkel von 60^o steht und damit den Berührpunkt des Kreises mit dem Dreieck trifft.

Dann bilden die Strecken a, b und c ein gleichseitiges Dreieck, also ist i = b/2. Aus dem Strahlensatz folgt, dass d = a = 1/2 ist. Damit ist e = $\sqrt{{(2\cdot \frac 12)^2 - (\frac 12)^2}}$ = ${\frac{{\sqrt{3}}}{{2}}}$ .

Die Seitenlänge eines dreieckigen Deckchens ist nach bekannter Formel ${\frac{{2}}{{\sqrt{3}}}}$ , also ist f = ${\frac{{1}}{{\sqrt{3}}}}$ = ${\frac{{\sqrt{3}}}{{3}}}$ .

Es ergeben sich damit in folgenden Fällen folgende Tisch-Mindestlängen:

Anordnung	Länge
Kreis-Dreieck-Kreis-Dreieck-Kreis	${\frac{1}{2}}$ + 4^. ${\frac{{\sqrt{3}}}{{2}}}$ + ${\frac{1}{2}}$ $\approx$ 4, 464
Kreis-Dreieck-Dreieck-Kreis-Kreis	${\frac{1}{2}}$ + ${\frac{{\sqrt{3}}}{{2}}}$ + ${\frac{{\sqrt{3}}}{{3}}}$ + ${\frac{{\sqrt{3}}}{{2}}}$ + ${\frac{3}{2}}$ $\approx$ 4, 309
Dreieck-Kreis-Kreis-Dreieck-Kreis	${\frac{{\sqrt{3}}}{{3}}}$ + ${\frac{{\sqrt{3}}}{{2}}}$ + 1 + 2^. ${\frac{{\sqrt{3}}}{{2}}}$ + ${\frac{1}{2}}$ $\approx$ 4, 675
Dreieck-Kreis-Dreieck-Kreis-Kreis	wie eben: $\approx$ 4, 675
Dreieck-Dreieck-Kreis-Kreis-Kreis	2^. ${\frac{{\sqrt{3}}}{{3}}}$ + ${\frac{{\sqrt{3}}}{{2}}}$ + 2, 5 $\approx$ 4, 521

$\includegraphics[height=80mm]{l32}$

Die zweite Anordnung ist also die beste, ein möglichst kurzer Tisch ist damit etwas mehr (damit sich die Deckchen nicht berühren) als 4,309 Meter lang.

Man könnte nun noch untersuchen, ob ein Verdrehen der dreieckigen Deckchen noch für Verbesserung sorgt - es ist recht offensichtlich, dass das nicht der Fall sein wird, aber schwierig zu beweisen. Da wir bewusst nur nach einem möglichst kurzen Tisch gefragt hatten und die anderen Lösungen auch schon recht umfangreich sind, begnügen wir uns hier mit diesem Ergebnis.

Aufgabe 4

Stefan baut ein Mobile: Er sägt aus einem Holzbrett fünf kongruente Vierecke aus, markiert auf jedem Viereck denselben Punkt und befestigt an jedem der Vierecke eine Schnur am markierten Punkt. Anschließend befestigt Stefan vier der Vierecke mit ihren Schnüren an den vier Ecken des fünften. Er hebt die Konstruktion an der Schnur des fünften Vierecks in die Luft und stellt fest, dass alle Vierecke genau waagerecht hängen (wie das bei einem Mobile auch sein soll ...).

Zeige, dass Stefan kongruente Parallelogramme ausgeschnitten haben muss.

Lösung:

Wir übersetzen zunächst die Voraussetzungen der Aufgabenstellung in geometrische Aussagen. Dass die vier unten hängenden Holzteile waagerecht hängen, heißt, dass der Aufhängepunkt gleich dem Schwerpunkt des Vierecks (als Fläche gesehen) sein muss. An dem fünften, oberen Brett hängen noch an den Ecken die vier anderen Bretter, wodurch sich an der waagerechten Lage nichts ändert. Daraus folgt, dass der Aufhängepunkt auch gleich dem Schwerpunkt der vier Eckpunkte des Vierecks sein muss.

Gesucht ist also nach einem Viereck, bei dem der Schwerpunkt des Vierecks mit dem Schwerpunkt der vier Eckpunkte zusammenfällt. Daher überlegen wir uns als Erstes, wie man diese Schwerpunkte konstruieren kann.

Beim Dreieck ist der Schwerpunkt bekanntlich der Schnittpunkt der Seitenhalbierenden. Und zwar ist das dann gleichzeitig der Schwerpunkt des Dreiecks als Fläche als auch der Schwerpunkt der drei Eckpunkte. Bei einem Viereck fallen die Punkte offensichtlich nicht mehr in jedem Fall zusammen, denn wir können ja auf einer der Seiten eines Dreiecks einfach einen weiteren Punkt zufügen - an dem Schwerpunkt der Fläche ändert das nichts, wohl aber am Schwerpunkt der Eckpunkte, der dann zu dem neuen Punkt hingezogen wird.

Wir betrachten ein beliebiges Viereck ABCD. Den Schwerpunkt des Dreiecks ABC bezeichnen wir mit S_ABC. Der Schwerpunkt der vier Eckpunkte muss dann auf der Strecke S_ABCD liegen. (Genaugenommen liegt er auf dem Punkt S_P mit ${\frac{{\vert S_PS_{ABC}\vert}}{{\vert S_PD\vert}}}$ = ${\frac{1}{3}}$ , weil S_ABC dreimal so hoch gewichtet ist wie D. Die genaue Lage ist hier aber nicht mehr wichtig.)

$\begin{picture}(0,0)% \includegraphics{loes72_4.pstex}% \end{picture}$

@font

picture(2422,2566)(316,-2360) (2431,-556)(0,0)[lb] C% (316,-1096)(0,0)[lb] A% (1621,-2311)(0,0)[lb] B% (496, 74)(0,0)[lb] D% (1396,-691)(0,0)[lb] E% (1081,-376)(0,0)[lb] S_CDA% (1621,-1411)(0,0)[lb] S_ABC% (1536,-958)(0,0)[lb] S_ABCD% (839,-781)(0,0)[lb] S_P%

Um die Lage des Schwerpunktes S_ABCD des Vierecks zu bestimmen, betrachten wir noch den Schwerpunkt S_CDA des Dreiecks CDA. Die Dreiecke ABC und CDA stellen eine disjunkte Zerlegung des Vierecks ABCD dar, daher muss der Schwerpunkt von ABCD auf der Strecke S_ABCS_CDA liegen. (Genauso muss der Punkt S_ABCD auf der Strecke S_BCDS_DAB liegen, womit man ihn als den Schnittpunkt dieser beiden Strecken konstruieren kann; aber auch hier brauchen wir diese weitere Information für die Aufgabe nicht mehr.)

Damit liegen also S_ABC und S_ABCD = S_P = : X auf der Geraden (S_ABCD). Mit S_ABC und S_ABCD liegt aber auch S_CDA auf dieser Geraden; und mit D und S_CDA muss auch der Mittelpunkt E der Strecke AC auf der Geraden (S_ABCD) liegen (da er ja ein Seitenmittelpunkt des Dreiecks CDA - und auch des Dreiecks ABC - ist). Da nun schließlich E und S_ABC auf der Geraden liegen, muss auch B auf ihr liegen. Zusammengefasst ist die Gerade gleich der Geraden (BD), und die Diagonale AC wird von ihr in E geschnitten. Auf analoge Weise folgt, dass der Mittelpunkt von BD auf der Geraden (AC) liegt.

In unserem gesuchten Viereck schneiden sich also die Diagonalen in ihren Mittelpunkten.

Daraus folgt sofort (denn es ist | AE| = | CE| und | BE| = | DE|, und die von diesen Strecken eingeschlossenen Winkel sind jeweils Scheitelwinkel), dass die Dreiecke ABE und CDE kongruent sind, ebenso BCE und DAE. Folglich gilt | AB| = | CD| und | BC| = | DA|, womit ABCD ein Parallelogramm sein muss.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File