Beispiellösungen zu Aufgabenblatt 73

aktualisiert: 22. Oktober 2008

drucken Zum Ausdrucken als pdf-File oder als ps-File
Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.


Aufgabe 1


Es gilt bekanntlich $ {\frac{{1}}{{6}}}$ = 0, 1666... Gibt es noch weitere Brüche mit einstelligen Zählern und Nennern, für die

$\displaystyle {\frac{{a}}{{b}}}$ = 0, abbb...

gilt?


Lösung:


Gesucht sind alle a $ \in$ {0, 1,..., 9}, b $ \in$ {1,..., 9}, für die $ {\frac{{a}}{{b}}}$ = 0, abbb... gilt.


Zunächst stellen wir fest, dass für c $ \in$ {0, 1,..., 9} die Darstellung $ {\frac{{c}}{{90}}}$ = 0, 0cccc... gilt. Somit lässt sich

0, abbb...= $\displaystyle {\frac{{a}}{{10}}}$ + $\displaystyle {\frac{{b}}{{90}}}$

schreiben.


Daraus ergibt sich folgende äquivalente Aufgabenstellung:

Gesucht sind alle a $ \in$ {0, 1,..., 9}, b $ \in$ {1,..., 9} mit der Eigenschaft

    $\displaystyle {\frac{{a}}{{b}}}$ = $\displaystyle {\frac{{a}}{{10}}}$ + $\displaystyle {\frac{{b}}{{90}}}$    
$\displaystyle \Leftrightarrow$        90a = 9ab + b2    
$\displaystyle \Leftrightarrow$        9a . (10 - b) = b2. (1)

Da nun 9 die linke Seite von ([*]) teilt, muss dies auch für die rechte Seite gelten, d. h. 9| b2. Daraus folgt 3| b, also b $ \in$ {3, 6, 9}.


In der folgenden Fallunterscheidung verwenden wir jeweils die Beziehung

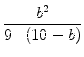a = $\displaystyle {\frac{{b^2}}{{9\cdot(10-b)}}}$,

die sich aus ([*]) ergibt.


1. Fall: b = 3.
Dann ist a = $ {\frac{{3^2}}{{9\cdot(10-3)}}}$ = $ {\frac{{9}}{{9\cdot 7}}}$ = $ {\frac{{1}}{{7}}}$ $ \notin${0,..., 9}.


2. Fall: b = 6.
Dann ist a = $ {\frac{{6^2}}{{9\cdot(10-6)}}}$ = 1. Dies ist das als Beispiel gegebene Zahlenpaar.


3. Fall: b = 9.
Dann ist a = $ {\frac{{9^2}}{{9\cdot(10-6)}}}$ = 9. Und in der Tat gilt $ {\frac{{9}}{{9}}}$ = 1 = 0, 999...


Bemerkung: Die Darstellung 0, 999... der Zahl 1 ist wohldefiniert. Allerdings muss man sich bewusst sein, dass durch sie die Zahlendarstellung nicht mehr eindeutig ist. Deshalb kann die Vereinbarung zweckmäßig sein, nur eine der beiden Darstellungen 1 und 0, 999... zu benutzen - wenn man denn die Wahl hat. Nach Aufgabenstellung muss man hier die Darstellung 0, 999... wählen und somit ergeben sich genau zwei Zahlenpaare mit der gesuchten Eigenschaft.


Aufgabe 2


Karl ist Gärtner und hat ein Blumenbeet, das gleichmäßig mit acht mal acht roten Blumen bepflanzt ist. Um etwas Abwechslung ins Beet zu bekommen, möchte er einige der roten Blumen durch blaue ersetzen, und zwar so, dass sich ein vollständiges blaues Blumenrechteck ergibt. Wie viele solcher Rechtecke gibt es?


Lösung:


Um die Aufgabenstellung etwas zu präzisieren: Die Kanten des blauen Blumenrechtecks sollten natürlich parallel zu den Kanten des Blumenbeets liegen. (*)

Karl kann die Position und Größe des blauen Blumenrechtecks eindeutig bestimmen, indem er vier Geraden im Beet verteilt, und zwar so, wie es die Abbildung zeigt (zwischen den Blumenreihen bzw. -spalten oder am Rand des Beetes):

\includegraphics[height=50mm]{blumen}

Für die Platzierung der ersten horizontalen Geraden hat Karl 9 Möglichkeiten. Da die zweite horizontale Gerade nicht direkt auf der ersten liegen soll (denn sonst hätte unser blaues Blumenrechteck keine Ausdehnung) und die Reihenfolge der Verteilung keine Rolle spielt, hat er insgesamt $ {\frac{{9 \cdot 8}}{{2}}}$ Möglichkeiten, diese beiden horizontalen Geraden zu platzieren. Danach hat er - unabhängig von der Wahl der horizontalen Geraden - auch $ {\frac{{9 \cdot 8}}{{2}}}$ Möglichkeiten, die beiden vertikalen Geraden zu platzieren.

Insgesamt erhalten wir durch Multiplikation dieser beiden Anzahlen

$\displaystyle {\frac{{9 \cdot 8}}{{2}}}$ . $\displaystyle {\frac{{9 \cdot 8}}{{2}}}$ = 362 = 1296

verschiedene Möglichkeiten für das blaue Blumenrechteck.


Bemerkung: (*) So, wie wir die Aufgabe formuliert hatten, wäre es auch möglich - insbesondere wenn man Blumen als Punkte ansieht -, Rechtecke zu finden, deren Kanten im 45-Grad-Winkel zu den Beetkanten stehen. Da waren wir etwas ungenau - eigentlich hätten wir von Blumen sprechen müssen, deren Blüten quadratisch sind und die sich jeweils berühren. Denn die erste Formulierung der Aufgabe war diejenige, dass Rechtecke auf einem Schachbrett zu suchen waren, was uns aber zu langweilig erschien ...


Aufgabe 3


Ein Frosch sitzt an einer Ecke eines Tetraeders. Am Ende jeder Minute entscheidet er sich für eine der benachbarten Ecken und springt dorthin. Mit welcher Wahrscheinlichkeit (exakt!) sitzt der Frosch nach genau einem Tag wieder an seiner Ausgangsecke?


Lösung:


Wir bezeichnen die Tetraederecke, auf der der Frosch am Anfang sitzt, mit A, die anderen Ecken mit B, C und D.

Als Erstes können wir feststellen, dass aus Symmetriegründen zu jedem Zeitpunkt die Wahrscheinlichkeiten für den Aufenthalt des Frosches bei B, C und D gleich sind. Daher fassen wir sinnvollerweise diese Wahrscheinlichkeiten zur Wahrscheinlichkeit pi(BCD) zusammen, die dafür steht, dass er sich auf B, C oder D aufhält - i bezeichnet dabei die betrachtete Minute. Mit pi(A) sei entsprechend die Wahrscheinlichkeit für einen Aufenthalt bei A benannt. Außerdem ist klar, dass immer gilt: pi(A) + pi(BCD) = 1.

Nun hat der Frosch folgende Möglichkeiten, zum Punkt A zu springen: Er muss auf einem der drei Punkte B, C oder D stehen und sich von den jeweils genau drei Möglichkeiten den Sprung nach A aussuchen. Daher gilt für jede Minute i:

pi+1(A) = $\displaystyle {\textstyle\frac{1}{3}}$pi(B) + $\displaystyle {\textstyle\frac{1}{3}}$pi(C) + $\displaystyle {\textstyle\frac{1}{3}}$pi(D) = $\displaystyle {\textstyle\frac{1}{3}}$pi(BCD) (2)

Nun schauen wir uns die Wahrscheinlichkeiten für die ersten Minuten an:

Minute i Aufenthaltswahrscheinlichkeit
  pi(A) pi(BCD)
0 1   = $\displaystyle {\textstyle\frac{1}{4}}$ + $\displaystyle {\textstyle\frac{3}{4}}$ 0   = $\displaystyle {\textstyle\frac{3}{4}}$ - $\displaystyle {\textstyle\frac{3}{4}}$
1 0   = $\displaystyle {\textstyle\frac{1}{4}}$ - $\displaystyle {\textstyle\frac{1}{4}}$ 1   = $\displaystyle {\textstyle\frac{3}{4}}$ + $\displaystyle {\textstyle\frac{1}{4}}$
2 $\displaystyle {\textstyle\frac{1}{3}}$   = $\displaystyle {\textstyle\frac{1}{4}}$ + $\displaystyle {\frac{{1}}{{3\cdot 4}}}$ $\displaystyle {\textstyle\frac{2}{3}}$   = $\displaystyle {\textstyle\frac{3}{4}}$ - $\displaystyle {\frac{{1}}{{3\cdot 4}}}$
3 $\displaystyle {\textstyle\frac{2}{9}}$   = $\displaystyle {\textstyle\frac{1}{4}}$ - $\displaystyle {\frac{{1}}{{3^2\cdot 4}}}$ $\displaystyle {\textstyle\frac{7}{9}}$   = $\displaystyle {\textstyle\frac{3}{4}}$ + $\displaystyle {\frac{{1}}{{3^2\cdot 4}}}$
4 $\displaystyle {\frac{{7}}{{27}}}$   = $\displaystyle {\textstyle\frac{1}{4}}$ + $\displaystyle {\frac{{1}}{{3^3\cdot 4}}}$ $\displaystyle {\frac{{20}}{{27}}}$   = $\displaystyle {\textstyle\frac{3}{4}}$ - $\displaystyle {\frac{{1}}{{3^3\cdot 4}}}$
5 $\displaystyle {\frac{{20}}{{81}}}$   = $\displaystyle {\textstyle\frac{1}{4}}$ - $\displaystyle {\frac{{1}}{{3^4\cdot 4}}}$ $\displaystyle {\frac{{61}}{{81}}}$   = $\displaystyle {\textstyle\frac{3}{4}}$ + $\displaystyle {\frac{{1}}{{3^4\cdot 4}}}$

Man erkennt zum einen, dass sich für jede einzelne Tetraederecke die Werte recht schnell dem Wert 1/4 nähern. Und wenn man davon inspiriert die genauen Werte als Abweichung davon angibt, erkennt man eine schöne Regelmäßigkeit:

Wenn zur Minute i gilt: pi(A) = $ {\frac{1}{4}}$ + $ {\frac{{1}}{{3^{i-1}\cdot 4}}}$, dann gilt automatisch pi(BCD) = $ {\frac{3}{4}}$ - $ {\frac{{1}}{{3^{i-1}\cdot 4}}}$; nach dem oben Gesagten ([*]) folgt pi+1(A) = $ {\frac{1}{4}}$ - $ {\frac{{1}}{{3^{i}\cdot 4}}}$. Und entsprechend gilt noch eine Minute später pi+2(A) = $ {\frac{1}{4}}$ + $ {\frac{{1}}{{3^{i+1}\cdot 4}}}$. Damit ist gezeigt, dass sich das Muster immer weiter so fortsetzt. Nach einem Tag = 1440 Minuten ist daher

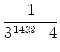
p1440(A) = $\displaystyle {\textstyle\frac{1}{4}}$ + $\displaystyle {\frac{{1}}{{3^{1439}\cdot 4}}}$ $\displaystyle \approx$ $\displaystyle {\textstyle\frac{1}{4}}$ + 10-687.


Aufgabe 4


Ein 120 Meter langes Seil ist an den Spitzen zweier 50 Meter bzw. 100 Meter hoher Bäume befestigt. Die beiden Bäume stehen 100 Meter voneinander entfernt.

An dem Seil ist eine bewegliche Rolle befestigt, mit deren Hilfe der kleine, mutige Klaus, an der Rolle hängend, vom höheren zum niedrigeren Baum gelangen will. Bei dieser Bewegung ist das Seil stets von der aktuellen Rollenposition zu den Befestigungsenden an den Bäumen straff gespannt.

Welches ist die kleinste Höhe über dem Erdboden, die Klaus bei seiner akrobatischen Übung haben wird? Der kleine Klaus misst übrigens bei nach oben gestreckten Armen gerade mal 2 Meter.


Lösung:


Bei dieser Aufgabe ist es sehr hilfreich, ein paar Tatsachen über Ellipsen zu kennen. Zunächst einmal ist eine Ellipse ja, entsprechend ihrer Definition als Ortskurve, die Menge aller Punkte, die von zwei festen Punkten A und B eine konstante Abstandssumme haben.

Das bedeutet aber für unsere Aufgabe, dass, da das Seil stets zu den Baumspitzen (sie seien mit A und B bezeichnet - und die Fußpunkte der Bäume FA und FB) straff gespannt ist, sich die Rolle auf einem Ellipsenbogen bewegt - die Summe der Abstände der Rollenposition zu den beiden Punkten A und B ist zu jedem Zeitpunkt 120 Meter. Die beiden Punkte A und B werden dann übrigens die Brennpunkte der zugehörigen Ellipse genannt.

\includegraphics[]{ellipse_bearb}
Es ist also der ,,tiefste`` Punkt P dieses Ellipsenbogens gesucht. In diesem tiefsten Punkt P lässt sich eine waagerechte Tangente, im Bild die Gerade (RS), an den Ellipsenbogen legen.

Nun benutzen wir eine weitere bemerkenswerte Eigenschaft der Ellipsen: Sendet man einen Lichtstrahl von einem der Brennpunkte zum Rand der Ellipse und wird dieser dort entsprechend des Reflexionsgesetzes an der Ellipse bzw. genauer: an der dortigen Tangente reflektiert, so geht der reflektierte Strahl durch den anderen Brennpunkt. Exakt mathematisch formuliert ist also die Normale der Ellipse in einem Ellipsenpunkt stets die Symmetrieachse der beiden Verbindungsgeraden dieses Punktes zu den Brennpunkten.

In unserem Fall bedeutet dies nun, dass der Spiegelpunkt B' von B an der Geraden (RS) genau auf der Verlängerung der Geraden (AP) liegen muss, denn es gilt ja $ \angle$APR = $ \angle$SPB = $ \angle$B'PS. Gleichzeitig ergibt sich damit übrigens, dass der tiefste Punkt zwischen den Bäumen erreicht wird, das heißt, dass die Skizze in dieser Form korrekt ist.

Da außerdem | PB'| = | PB| ist, gilt | AB'| = 120 m, und deswegen folgt nach Satz des Pythagoras im Dreieck ACB' mit der Bezeichnung | BS| = x (alles in Metern):

1202 = | AB'|2 = | AC|2 + | CB'|2 = (50 + 2x)2 + 1002 = 502 + 200x + 4x2 + 1002.

Dies bedeutet umgeformt: x2 + 50x - 475 = 0. Diese quadratische Gleichung hat als einzige positive Lösung x = - 25 + 10 . $ \sqrt{{11}}$ $ \approx$ 8, 17 (Meter). Demnach sind Klaus' Füße am niedrigsten Punkt 50 - (- 25 + 10$ \sqrt{{11}}$) = 75 - 10$ \sqrt{{11}}$ $ \approx$ 39, 83 Meter über dem Erdboden.


Ein alternativer - und elementarer Lösungsweg
Auch wenn man die besondere Spiegelungseigenschaft der Ellipse nicht kennt, kann man zur Lösung gelangen, und zwar mit elementaren Ideen - eigentlich beweist man damit gerade die genannte Eigenschaft der Ellipse.

Sei P die Position der Rolle zu einem (fast) beliebigen Zeitpunkt, mit A und B seien wieder die Baumspitzen benannt. (DE) sei die Gerade durch P, die parallel zum Erdboden verläuft. Offensichtlich ist es möglich, dass Klaus unterhalb der Höhe von B hängt, also können wir unsere Überlegungen auf diesen Fall einschränken. (Das dient nur dazu, lästige Fallunterscheidungen zu vermeiden.) Wir spiegeln (,,wieder``) die Strecke PB an (DE) und erhalten die Strecke P$ \tilde{{B}}$. Die Entfernung | BE| heiße $ \tilde{{x}}$. Dann ist

| A$\displaystyle \tilde{{B}}$| = $\displaystyle \sqrt{{(50+2\tilde{x})^2 + 100^2}}$. (3)

$ \tilde{{x}}$ gibt nach Definition an, wie tief der kleine Klaus unter der Baumspitze B hängt. Dieser Wert wird nach Gleichung ([*]) genau dann maximal, wenn | A$ \tilde{{B}}$| seinen maximalen Wert annimmt. Nach der Dreiecksungleichung gilt:

| A$\displaystyle \tilde{{B}}$| $\displaystyle \leq$ | AP| + | P$\displaystyle \tilde{{B}}$| = | AP| + | PB| = 120. (4)

\includegraphics[]{ellzwo_bearb}
Diesen Wert kann man aber auch wirklich erreichen: Wir wählen B' so auf dem Baumstamm des rechten Baumes, dass | AB'| = 120 gilt. Nach Pythagoras liegt dann B' genau $ \sqrt{{120^2-100^2}}$ = $ \sqrt{{4400}}$ = 20 . $ \sqrt{{11}}$ $ \approx$ 66, 33 Meter unterhalb der Baumspitze A, also $ \hat{{x}}$ : = 20 . $ \sqrt{{11}}$ - 50 $ \approx$ 16, 3 Meter unterhalb von B. Nun betrachten wir den Punkt P*, der x : = $ \hat{{x}}$/2 Meter unterhalb von B auf der Strecke AB' liegt. Er hat offensichtlich von B denselben Abstand wie von B'; nach Konstruktion von B' gehört er somit zur Bahn der Rolle, an der Klaus hängt. Und da, wie schon angekündigt, mit ihm Gleichheit in ([*]) erreicht wird, ist kein Punkt tiefer als er, und wenn man es sich etwas genauer überlegt, sieht man auch leicht, dass dies der einzige solche Punkt ist.

drucken Zum Ausdrucken als pdf-File oder als ps-File