Aufgabenblatt 40

aktualisiert: 24. November 2004

Aufgabe 1

Bei den Jugendfeuerwehrspielen in Fleckendorf gibt es für einen der Teilnehmer folgende Aufgabe zu bewältigen:

Eine Wasserleitung soll so lange wie möglich ununterbrochen mit Wasser versorgt werden. Die Leitung wird über einen Trichter befüllt, in den 5 Liter passen. Aus ihm läuft in 10 Sekunden genau 1 Liter Wasser in die Leitung. Als Nachschub stehen in einer langen Reihe, jeweils mit 5 m Abstand, gefüllte 5-Liter-Wassereimer bereit. Beim Holen der Eimer geht man erfahrungsgemäß genau einen Meter pro Sekunde (die Eimer sind ja schwer ...) und man darf immer nur einen Eimer zur Zeit schleppen. Dafür geht das Befüllen sehr schnell. Zu Beginn steht man am Trichter und hat bereits einen 5-Liter-Eimer in der Hand, den man zum Start in den Trichter entleert.


\includegraphics[width=10cm]{eimer.eps}

  1. Wie lange kann man das Wasser ununterbrochen fließen lassen?
  2. Wie lange geht es, wenn der Einfülltrichter 10 Liter fasst?
  3. Und wie ist es, wenn er 15 Liter fasst?

Aufgabe 2

Drei Mathematiker unterhalten sich:


Thomas sagt: ,,Ist 32 nicht eine schöne Zahl? Berechnet man die dritte Potenz dieser Zahl, also 323 = 32768, so sieht man, dass das Ergebnis ebenfalls mit 32 beginnt.``


Ulrich sagt: ,,Mal was anderes: Ich vermute, dass die Dezimaldarstellung jeder der Zahlen $ \sqrt[k]{{10}}$ mit k $ \geq$ 2 unendlich viele Neunen enthält!``


Benno sagt: ,,Wenn Ulrich mit seiner Vermutung Recht hat, dann gibt es unendlich viele schöne Zahlen, die nicht durch 10 teilbar sind, und ich kann euch zeigen, wie man beliebig große schöne Zahlen berechnen kann!``
  1. Zeige, dass Benno die Wahrheit sagt!
  2. Auch für höhere Exponenten gibt es schöne Zahlen, denn zum Beispiel ist

    464164 = 4641633499322843136    und    146787 = 146780439427525678437261283712.

    Zeige: Wenn Ulrich Recht hat, dann gibt es zumindest für jeden der Exponenten 3, 4, 5,..., 10 unendlich viele schöne Zahlen, die nicht durch 10 teilbar sind!

Aufgabe 3

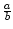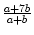Ausgehend von einem beliebigen positiven Bruch $ {\frac{{a}}{{b}}}$ bildet Stephan den Bruch $ {\frac{{a+7b}}{{a+b}}}$ und wiederholt diese Prozedur einige Male. Überrascht stellt er fest, dass sich sehr bald der Wert des Bruches kaum mehr ändert!
  1. Welchem Wert nähern sich die Brüche bei wiederholter Ausführung der Prozedur? (Anders gesagt: Gegen welchen Wert konvergiert die Folge der Brüche?)
  2. Wie ist die Antwort, wenn man in der Prozedur die Zahl ,,7``durch irgendeine andere nichtnegative Zahl n ersetzt?
  3. Was geschieht für negative n?

Aufgabe 4

Konrad sagt zu Jonathan: ,,Hier habe ich ein Quadrat ABCD mit Seitenlänge 1. In Gedanken habe ich darin achsenparallel ein zweites Quadrat versteckt. Du sollst herausfinden, wo dessen Mittelpunkt liegt.``

Jonathan erwidert: ,,Sag mir wenigstens, ob die Strecke EF (die die Seitenmitten von AD und BC verbindet) das Quadrat schneidet.``

Daraufhin Konrad: ,,Sie schneidet das Quadrat in zwei Punkten S und T, wobei S näher an E liegt als T. Ich sage dir zwar nicht, wo genau diese Schnittpunkte liegen, aber es gilt 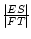$ {\frac{{\vert ES\vert}}{{\vert FT\vert}}}$ = 1/4.``

Wo kann jetzt noch der Mittelpunkt des Quadrates liegen?


\includegraphics[width=4cm]{kreisspiel2.eps}


Jonathan fragt weiter: ,,Und wie ist es mit der Strecke GH (sie liegt parallel zur Seite AD und hat von ihr den Abstand 2/5)?``

Konrad antwortet: ,,Auch sie schneidet das kleine Quadrat, und zwar in zwei Punkten U (näher an G) und V, und der Bruch $ {\frac{{\vert GU\vert}}{{\vert HV\vert}}}$ hat den Wert 2/3.``

Wie sieht die Situation mit dieser weiteren Information aus?

Einsendetermin ist der 20. 12. 2004

Mathematisches Institut
Mathematischer Korrespondenzzirkel
Bunsenstraße 3-5, 37073 Göttingen

drucken Zum Ausdrucken als pdf-File oder als ps-File