 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Aufgabe 1
Bei den Jugendfeuerwehrspielen in Fleckendorf gibt es für einen der Teilnehmer
folgende Aufgabe zu bewältigen:
Eine Wasserleitung soll so lange wie möglich ununterbrochen mit Wasser versorgt werden. Die Leitung wird über einen Trichter befüllt, in den 5 Liter passen. Aus ihm läuft in 10 Sekunden genau 1 Liter Wasser in die Leitung. Als Nachschub stehen in einer langen Reihe, jeweils mit 5 m Abstand, gefüllte 5-Liter-Wassereimer bereit. Beim Holen der Eimer geht man erfahrungsgemäß genau einen Meter pro Sekunde (die Eimer sind ja schwer ...) und man darf immer nur einen Eimer zur Zeit schleppen. Dafür geht das Befüllen sehr schnell. Zu Beginn steht man am Trichter und hat bereits einen 5-Liter-Eimer in der Hand, den man zum Start in den Trichter entleert.
![\includegraphics[width=10cm]{eimer.eps}](img1.png)
- Wie lange kann man das Wasser ununterbrochen fließen lassen?
- Wie lange geht es, wenn der Einfülltrichter 10 Liter fasst?
- Und wie ist es, wenn er 15 Liter fasst?
Lösung:
Zuerst nummerieren wir die Eimer so, dass der Eimer direkt beim Trichter die 0, der nächste die 1 usw. erhält.
- 1.
- Da der Trichter, wenn man kein Wasser nachfüllt, nach spätestens 50 s leer
ist, kann man zwischen zwei Befüllungen nicht weiter als
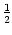 . 5s . 1m/s = 25m und zurück laufen. Man
erreicht also alle Eimer bis zum fünften; das Wasser läuft
6 . 50s = 300s = 5min lang.
. 5s . 1m/s = 25m und zurück laufen. Man
erreicht also alle Eimer bis zum fünften; das Wasser läuft
6 . 50s = 300s = 5min lang.
- b)+c)
- Nach dieser Argumentation kann man bei dem Zehn-Liter-Trichter
nicht weiter als bis zum Eimer Nummer 10 kommen. Tatsächlich erreicht man aber bei allen Trichtern mit einem Fassungsvermögen ab neun Litern nur zehn Eimer einschließlich des Eimers an nullter Position: In der Zeit, die benötigt wird, um einen Eimer mit der Nummer n > 5 zu holen, läuft mehr Wasser durch den Trichter, als man nachfüllen kann, der ,,Verlust`` liegt bei n - 5 Litern. Umgekehrt kann man mit Eimern n < 5 einen ,,Vorrat`` anlegen, der jeweils 5 - n Liter beträgt. Insgesamt kann man also zehn Liter (4 + 3 + 2 + 1) ,,Vorrat`` anlegen, aber genauso viel verbraucht man auch beim Holen der Eimer 6 bis 9. In der Tat ist es möglich, diese auf theoretischem Wege gefundene Grenze von zehn genutzten Eimern zu erreichen, z. B. indem man immer (für 1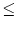 n
n 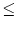 4) nach dem
(5 - n)-ten Eimer den (5 + n)-ten Eimer holt. Das Wasser läuft dann also
10 . 50s = 500s = 8min 20s
lang.
4) nach dem
(5 - n)-ten Eimer den (5 + n)-ten Eimer holt. Das Wasser läuft dann also
10 . 50s = 500s = 8min 20s
lang.
Aufgabe 2
Drei Mathematiker unterhalten sich:
Thomas sagt: ,,Ist 32 nicht eine schöne Zahl? Berechnet man die dritte Potenz dieser Zahl, also 323 = 32768, so sieht man, dass das Ergebnis ebenfalls mit 32 beginnt.``
Ulrich sagt: ,,Mal was anderes: Ich vermute, dass die Dezimaldarstellung jeder der Zahlen
Benno sagt: ,,Wenn Ulrich mit seiner Vermutung Recht hat, dann gibt es unendlich viele schöne Zahlen, die nicht durch 10 teilbar sind, und ich kann euch zeigen, wie man beliebig große schöne Zahlen berechnen kann!``
- Zeige, dass Benno die Wahrheit sagt!
- Auch für höhere Exponenten gibt es schöne Zahlen, denn zum
Beispiel ist
464164 = 4641633499322843136 und146787 = 146780439427525678437261283712.Zeige: Wenn Ulrich Recht hat, dann gibt es zumindest für jeden der Exponenten 3, 4, 5,..., 10 unendlich viele schöne Zahlen, die nicht durch 10 teilbar sind!
Lösung:
Wir zeigen gleich Aufgabenteil b), da aus diesem Bennos Aussage folgt. Hierzu
geben wir eine explizite Vorschrift an, wie man schöne, nicht auf Null
endende Zahlen für einen
Exponenten k mit
3 ![]() k
k ![]() 10 konstruieren kann. Sei also ein solches k
gegeben. Betrachte die Zahl
x =
10 konstruieren kann. Sei also ein solches k
gegeben. Betrachte die Zahl
x = ![]() . Wenn Ulrichs Aussage stimmt,
findet man in der Dezimaldarstellung von x unendlich viele Neunen. Anders
formuliert bedeutet das, dass in der Dezimalzahl
10n . x für unendlich viele
n die Ziffer 9 direkt vor dem Komma steht. Das heißt aber, dass
. Wenn Ulrichs Aussage stimmt,
findet man in der Dezimaldarstellung von x unendlich viele Neunen. Anders
formuliert bedeutet das, dass in der Dezimalzahl
10n . x für unendlich viele
n die Ziffer 9 direkt vor dem Komma steht. Das heißt aber, dass
Wir behaupten nun, dass unter den unendlich vielen so konstruierten Zahlen a unendlich viele schöne Zahlen zu finden sind.
Es gilt ja zum einen sicher
| ak | = | a . ak-1 | |
| < | a . |
||
| = | a . |
||
| = | a . 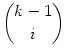 . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i |
Nun trennen wir den ersten Summanden dieser Summe ab und benutzen k
| ak | < | a . 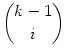 . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i |
|
| = | a . 10(n-1)(k-1)+1 | ||
+ a . 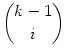 . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i . 10(k-1-i)(n-1) . 10(k-1-i)/(k-1) . 10-i |
|||
| < | a . 10(n-1)(k-1)+1 | ||
| + (x . 10n-1 + 1/10) . |
|||
| = | a . 10(n-1)(k-1)+1 + |
||
| + |
Wir behaupten nun, dass
Das erste Beispiel ist übrigens nicht aus
![]() , sondern nach
derselben Idee aus
, sondern nach
derselben Idee aus
![]() entstanden.
entstanden.
![]() hat am Anfang
keine genügend hohen Ziffern, das erste daraus sich ergebende Bespiel ist
siebenstellig.
hat am Anfang
keine genügend hohen Ziffern, das erste daraus sich ergebende Bespiel ist
siebenstellig.
Aufgabe 3
Ausgehend von einem beliebigen positiven Bruch
![]() bildet Stephan den
Bruch
bildet Stephan den
Bruch
![]() und wiederholt diese Prozedur einige
Male. Überrascht stellt er fest, dass sich sehr bald der Wert des Bruches
kaum mehr ändert!
und wiederholt diese Prozedur einige
Male. Überrascht stellt er fest, dass sich sehr bald der Wert des Bruches
kaum mehr ändert!
- Welchem Wert nähern sich die Brüche bei wiederholter Ausführung der Prozedur? (Anders gesagt: Gegen welchen Wert konvergiert die Folge der Brüche?)
- Wie ist die Antwort, wenn man in der Prozedur die Zahl ,,7``durch irgendeine andere nichtnegative Zahl n ersetzt?
- Was geschieht für negative n?
Lösung:
- Zum Test beginnen wir mit dem Bruch
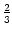 . Dann ergeben sich
schrittweise folgende Brüche:
. Dann ergeben sich
schrittweise folgende Brüche:
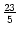 ,
,
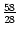 ,
,
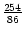 ,
,
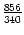 ,
,
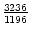 ,
,
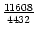 ,
,
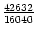 ,
,
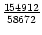 ,
,
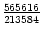 , ..., bzw. in Dezimalbruchschreibweise
0, 6666...,
4, 6,
2, 0714...,
2, 9534...,
2, 5176...,
2, 7056...,
2, 6191...,
2, 6578...,
2, 6403...,
2, 6482... usw.
, ..., bzw. in Dezimalbruchschreibweise
0, 6666...,
4, 6,
2, 0714...,
2, 9534...,
2, 5176...,
2, 7056...,
2, 6191...,
2, 6578...,
2, 6403...,
2, 6482... usw.
Die Werte scheinen sich also einer Zahl bei etwa 2, 64 zu nähern. Nur welcher Zahl ganz genau?
Nehmen wir einmal an (und das dürfen wir entsprechend der Aufgabenstellung), dass sich die Folge der Brüche der Zahl x beliebig nähert, also gegen x konvergiert. Dann ist also x
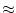
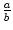 für jedes Glied
für jedes Glied
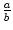 der Folge, welches weit hinten in der Folge steht. Aber auch das
nächste Glied, nämlich
der Folge, welches weit hinten in der Folge steht. Aber auch das
nächste Glied, nämlich
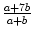 , ist dann nahe an
x. Somit muss zwangsläufig
, ist dann nahe an
x. Somit muss zwangsläufig
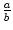
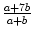 sein. Da das
,,nahe``in der Tat beliebig nahe sein kann, gilt im Grenzwert
tatsächlich
Umgeformt bedeutet dies aber a2 + ab = ab + 7b2 bzw. a2 = 7b2. Demnach ist x =
sein. Da das
,,nahe``in der Tat beliebig nahe sein kann, gilt im Grenzwert
tatsächlich
Umgeformt bedeutet dies aber a2 + ab = ab + 7b2 bzw. a2 = 7b2. Demnach ist x =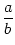 =
= 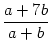 = x.
= x.
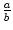 =
= 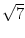
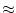 2, 6458.
2, 6458.
Das ist also der gesuchte Wert.
Diese etwas heuristische Herleitung kann man mit Mitteln der Analysis auch mathematisch exakt aufschreiben: Nennt man die Folgenglieder xn =
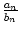 und
geht man davon aus, dass die Folge (xn) gegen x konvergiert, so gilt
und
geht man davon aus, dass die Folge (xn) gegen x konvergiert, so gilt
x = 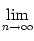 xn
xn= 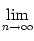 xn+1
xn+1= 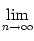
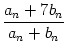
= 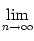
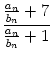
= 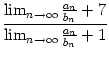
= 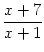 .
.
Also gilt x =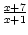 , was umgeformt
x = ±
, was umgeformt
x = ±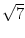 ergibt. Da offenbar
alle Folgenglieder positiv sind, kommt nur
x =
ergibt. Da offenbar
alle Folgenglieder positiv sind, kommt nur
x = 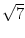 in Frage.
in Frage.
- Es ist nicht schwer zu sehen, dass die Herleitung in Teil a) für jede
nicht negative ganze (oder auch reelle) Zahl n als Ergebnis
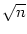 liefert. Man ersetze im Text oben einfach jede auftretende 7 durch n.
liefert. Man ersetze im Text oben einfach jede auftretende 7 durch n.
- Für negative n nähern sich die Brüche keiner Zahl. Die Folge
divergiert also. Dies sieht man am schnellsten so ein:
Angenommen, die Folge würde auch für ein negatives n gegen eine Zahl x konvergieren. Dann würde dieselbe Herleitung wie oben zeigen, dass x2 = n gelten müsste. Das ist aber für negative n in reellen Zahlen nicht lösbar.
Als Beispiel betrachtet man die Folge für n = - 1 mit dem Startwert
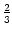 . Hier beginnt sie mit den Gliedern
. Hier beginnt sie mit den Gliedern
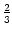 ,
,
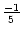 ,
,
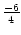 ,
,
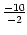 ,
,
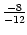 ,
,
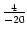 ,
,
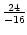 ,
,
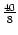 ,
,
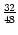 , ...
, ...
Die Folge ist also periodisch mit Periode
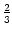 , -
, - 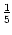 , -
, - 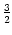 , 5.
Auch für n = - 3 ist sie periodisch (unabhängig vom Anfangsglied).
Für alle anderen negativen n ist sie nicht periodisch, sondern wechselt unendlich oft von beliebig großen zu beliebig kleinen Werten, ohne sich dabei je zu wiederholen.
, 5.
Auch für n = - 3 ist sie periodisch (unabhängig vom Anfangsglied).
Für alle anderen negativen n ist sie nicht periodisch, sondern wechselt unendlich oft von beliebig großen zu beliebig kleinen Werten, ohne sich dabei je zu wiederholen.
Bemerkung 2 (für Leser, die mit etwas linearer Algebra und den komplexen Zahlen vertraut sind): Betrachtet man zu jedem Bruch
![]() den Vektor
vk =
den Vektor
vk = ![]()
![]()
![]() und die Matrix
und die Matrix
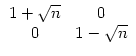
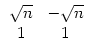
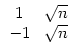
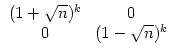
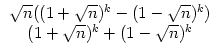
Wenn man dagegen als Startwerte a0 = 1 und b0 = 0 nimmt (das darf man dann vorläufig nur in der Vektorschreibweise deuten(!)), so erhält man
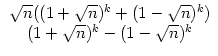
Durch Linearkombination erhält man für beliebige Startwerte a0 > 0 und
b0 > 0 die Folge der Brüche
| = | 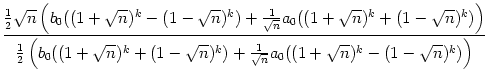 |
||
| = | 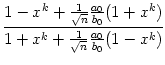 |
||
| = | 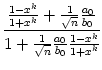 |
||
| = | 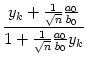 , , |
wobei x =
Ist nun n > 0, so ist x dem Betrage nach kleiner als 1 und daher konvergiert die Folge yk gegen 1, weswegen die Folge der Brüche gegen ![]() strebt (wie oben schon gesehen).
strebt (wie oben schon gesehen).
Ist n < 0 und erlaubt man das Rechnen mit komplexen Zahlen, so ist x eine solche komplexe Zahl, und zwar mit Betrag 1. Eine etwas detailliertere Analyse zeigt, dass x dann genau für n = - 1 und n = - 3 eine Einheitswurzel ist (die also xm = 1 für ein m > 0 erfüllt). Daher wird die Folge in genau diesen Fällen periodisch. In den anderen Fällen wandert die Folge xk den komplexen Einheitskreis entlang, ohne periodisch zu werden, und kommt dabei allen Werten auf dem Kreis unendlich oft beliebig nahe (die Folgenglieder liegen dicht auf dem Kreis). Hierbei variiert dann yk auf der imaginären Achse und kommt dort jedem Wert beliebig nahe. Daraus kann man dann aber schnell ersehen, dass auch die Folge der Brüche dicht auf der reellen Achse verteilt ist und dort also jedem Wert (irgendwann einmal) beliebig nahe kommt, insbesondere werden die Brüche unendlich oft beliebig groß und beliebig klein.
Aufgabe 4
Konrad sagt zu Jonathan: ,,Hier habe ich ein Quadrat ABCD mit
Seitenlänge 1. In Gedanken habe ich darin achsenparallel ein zweites Quadrat
versteckt. Du sollst herausfinden, wo dessen Mittelpunkt liegt.``
Jonathan erwidert: ,,Sag mir wenigstens, ob die Strecke EF (die die Seitenmitten von AD und BC verbindet) das Quadrat schneidet.``
Daraufhin Konrad: ,,Sie schneidet das Quadrat in zwei Punkten S und
T, wobei S näher an E liegt als T. Ich sage dir zwar nicht, wo genau
diese Schnittpunkte liegen, aber es gilt
![]() = 1/4.``
= 1/4.``
Wo kann jetzt noch der Mittelpunkt des Quadrates liegen?
![\includegraphics[width=4cm]{kreisspiel2.eps}](img96.png)
Jonathan fragt weiter: ,,Und wie ist es mit der Strecke GH (sie liegt parallel zur Seite AD und hat von ihr den Abstand 2/5)?``
Konrad antwortet: ,,Auch sie schneidet das kleine Quadrat, und zwar in
zwei Punkten U (näher an G) und V, und der Bruch
![]() hat
den Wert 2/3.``
hat
den Wert 2/3.``
Wie sieht die Situation mit dieser weiteren Information aus?
Lösung:
Bezeichnen wir zunächst die Seitenlänge des kleinen, versteckten Quadrates
mit a und die Länge der Strecke ES mit b. Wegen
![]() = 1/4
folgt daraus | FT| = 4b, und außerdem gilt, weil die Strecke EF parallel
zur Quadratseite AB ist, b + a + 4b = 1, also b = (1 - a)/5.
= 1/4
folgt daraus | FT| = 4b, und außerdem gilt, weil die Strecke EF parallel
zur Quadratseite AB ist, b + a + 4b = 1, also b = (1 - a)/5.
Der einfacheren Beschreibung wegen legen wir unsere Figur so in ein kartesisches Koordinatensystem, dass A auf (0, 0) und C auf (1, 1) zu liegen kommt. Der Mittelpunkt M des kleinen Quadrats liege dann auf (xM, yM). Mit obiger Rechnung ergibt sich
Da 0 < a < 1 gilt, folgt
Nun wird das kleine Quadrat nach Voraussetzung ja von EF in genau zwei Punkten geschnitten, daher muss yM -
Damit kann M noch genau in dem schraffierten Bereich der folgenden Figur liegen.
![\includegraphics[width=4cm]{kreisspiel2loes1.eps}](img111.png)
Nehmen wir jetzt die Informationen hinzu, die sich durch den Schnitt mit der Strecke GH ergeben. Analoge Überlegungen wie oben liefern die Beziehungen
und damit die folgende Figur (mit der vorher gefundenen in Hellgrau zum Vergleich).
![\includegraphics[width=4cm]{kreisspiel2loes2.eps}](img116.png)
Die Menge der noch möglichen Lagen von M ist aber bedeutend kleiner als der Schnitt dieser beiden Parallelogramme: Wir haben noch nicht bedacht, dass zu jedem Punkt in jedem Parallelogramm auch die Information vorhanden ist, wie groß a ist - und das muss natürlich zueinander passen.
Ganz leicht erkennen wir die Folgen daraus, indem wir a aus (![]() ) und
(
) und
(![]() ) eliminieren - dann erhalten wir die Geradengleichung
) eliminieren - dann erhalten wir die Geradengleichung
auf dieser Geraden muss M liegen.
Setzt man diese Beziehung in die oben gefundenen Doppelungleichungen
(![]() ), (
), (![]() ), (
), (![]() ) und (
) und (![]() ) ein, so erhält man
nacheinander
) ein, so erhält man
nacheinander
![\includegraphics[width=4cm]{kreisspiel2loes3.eps}](img124.png)
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
