Gibt es eine Quadratzahl, deren Quersumme 6 ist?
Hinweis: Die Quersumme einer Zahl ist die Summe ihrer Ziffern!
Lösung:
Es gibt keine Quadratzahl, deren Quersumme 6 ist.
Dazu erinnern wir uns an die Teilbarkeitsregeln für 3 und 9: Eine Zahl ist
genau dann durch 3 teilbar, wenn auch ihre Quersumme durch 3 teilbar ist.
Eine Zahl ist genau dann durch 9 teilbar, wenn auch ihre Quersumme durch 9
teilbar ist.
Wir nehmen an, wir hätten eine Quadratzahl n = m2 mit Quersumme 6.
Da die Quersumme 6 durch 3 teilbar ist, ist unsere Zahl n durch 3
teilbar.
Weil 3 eine Primzahl ist, muss schon m durch 3 teilbar sein, also kann
man mit
einer natürlichen Zahl k schreiben: m = 3k.
Damit ist
n = m2 = (3k)2 = 9k2 durch 9 teilbar.
Dann muss aber auch die Quersumme von n durch 9 teilbar sein.
6 ist nicht durch 9 teilbar, also gibt es keine Quadratzahl mit Quersumme
6.
Aufgabe 2
Beim Göttinger Altstadtfest sollen, wie in der Abbildung
angedeutet, zwei Schmuckbänder zwischen zwei Bäumen aufgehängt werden, und
zwar jeweils von der Spitze des einen Baums zum unteren Stammende des anderen Baums.
| Die Organisatoren des Festes sind nun ein wenig besorgt, denn es soll unter den Bändern wenigstens noch so viel Platz bleiben, dass ein Mensch darunter durchgehen kann. Zwar sind die Höhen der Bäume erst kürzlich bestimmt worden, nämlich x = 6m und y = 4m, aber der Abstand d der Bäume ist völlig unbekannt. |
![\includegraphics[width=55mm]{aufgaben_04.eps}](img1.png)
|
Muss man hierzu dem Vermessungsamt einen Auftrag erteilen oder kann man die Organisatoren vorher schon beruhigen?
Lösung:
Die Veranstalter brauchen sich keine Sorgen zu machen! Egal, wie weit die
Bäume voneinander entfernt stehen: dort, wo sich die Bänder kreuzen, sind sie
2,40 Meter über der Erde.
|
Zum Beweis benötigt man kaum mehr als die
Strahlensätze (nämlich für die Gleichungen ( |
![\includegraphics[width=55mm]{loes06_02.eps}](img2.png)
|
Nun gilt:
(
| = | 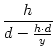 = = 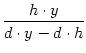 |
||
| = |
Hochmultiplizieren des Nenners
| xy - xh = hy | |||
| xy = h(x + y) |
und Auflösen nach h ergibt
Selbst wenn man davon ausgeht, dass die Schmuckbänder in Wirklichkeit noch ein wenig durchhängen, ist das völlig ausreichend dafür, dass noch ein Mensch darunter durchgehen kann.
Aufgabe 3
Bei dem Zahlenschloss an Peters Fahrrad muss man durch Drehen dreier
Rädchen, auf denen jeweils die Ziffern 1, 2 und 3 stehen, einen
dreiziffrigen Zahlencode einstellen, um das Schloss zu öffnen.
Angenommen, das
Schloss ist defekt und öffnet sich schon, wenn beliebige zwei der drei Ziffern
richtig eingestellt sind, wie viele Versuche braucht ein potentieller Dieb dann
höchstens (wenn er schlau ist!), um das Schloss zu öffnen?
Lösung:
Ein (wirklich schlauer!) potentieller Dieb kommt mit nur
fünf Versuchen aus.
Der Grund dafür, dass man überhaupt mit weniger als neun Versuchen
auskommen kann, ist folgender: Peters ursprünglicher Zahlencode sei
(A, B, C), wobei A, B, C jeweils eine der Ziffern 1, 2 oder 3
sind. Stellt der Dieb nun einen Versuchscode (a, b, c) ein und das Schloss
öffnet sich, ist er glücklich. Wenn es sich aber nicht öffnet, so kommen
auf einen Schlag sieben (!!!) mögliche Codes nicht mehr für (A, B, C) in
Frage, nämlich die Codes
(a, b, x), (a, x, c) und (x, b, c), wobei x wieder eine beliebige der
drei
Ziffern 1, 2 oder 3 ist. Wäre nämlich einer dieser Codes
gleich (A, B, C),
so hätte der Code (a, b, c) mit Peters Zahlencode (A, B, C) wenigstens
zwei
Ziffern gemeinsam, das defekte Schloss hätte sich also öffnen müssen.
Wie viele Möglichkeiten hat Peter überhaupt für seinen Code
(A, B, C)?
Für jede der drei Stellen kommen genau drei verschiedene Werte in Frage, also
gibt es genau 33 = 27 Möglichkeiten.
Davon kann der Dieb mit nur einem Versuch genau sieben ausschließen!
Insbesondere kann er das Schloss mit drei Versuchen höchstens zufällig,
aber
nicht sicher (und das war ja gefragt!) knacken, da er bis dahin
höchstens
3 . 7 = 21 Codes als Peters Zahlencode ausschließen kann. Ist
einer der übrigen 27 - 21 = 6 Codes der richtige, so hat sich das Schloss
nach den drei Versuchen noch nicht geöffnet.
Aber vier Versuche könnten doch theoretisch reichen, oder?
Schließlich sind
4 . 7 = 28 Codes mehr, als es überhaupt gibt, also muss
Peters Code dabeigewesen sein, oder?
Nein, leider nicht. Zwar kann der Dieb mit jedem der vier Versuche sieben Codes
ausschließen, aber diese müssen nicht alle verschieden
sein (und sind es auch nicht). Würde der Dieb zum Beispiel dummerweise
viermal
denselben Code versuchen, würde er trotzdem nur sieben und nicht
4 . 7 = 28 Codes ausschließen. Folgendermaßen sieht man, dass es bei vier
Versuchen
mindestens zwei solche Überschneidungen gibt, also wenigstens 27 - 28 + 2 = 1
möglicher Peter-Code unausgeschlossen bleibt:
Für die erste Stelle a eines Codes (a, b, c) hat man drei
Möglichkeiten.
Unter vier verschiedenen Codes C1, C2, C3 und C4
muss es also zwei geben,
die die gleiche erste Stelle haben. Sei also zum Beispiel
C1 = (a, b, c) und
C2 = (a, d, e). Dann sind unter den jeweils sieben Codes, die C1 und C2
ausschließen, auch die beiden (a, d, c) und (a, b, e), die von
beiden ausgeschlossen werden - man hat also mindestens zwei
Überschneidungen
unter den durch vier Versuche ausgeschlossenen Codes, und es werden insgesamt
nicht mehr als
4 . 7 - 2 = 26 Peter-Codes ausgeschlossen. Mit vier
Versuchen ist man also auch nicht auf der sicheren Seite, denn es könnte
immer noch einer der nicht ausgeschlossenen Codes der richtige sein; dann
bliebe
das Schloss nach diesen vier Versuchen geschlossen!
Dass es schließlich mit fünf Versuchen sicher klappt, zeigt man
zum Beispiel mit folgender Tabelle:
| Nr. | Code | Für den richtigen Code dadurch ausgeschlossen: |
| 1 | (1, 1, 2) | (1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 2, 2), (1, 3, 2), (2, 1, 2), (3, 1, 2) |
| 2 | (2, 2, 1) | (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 1, 1), (2, 3, 1), (1, 2, 1), (3, 2, 1) |
| 3 | (3, 3, 2) | (3, 3, 1), (3, 3, 2), (3, 3, 3), (3, 2, 2), (2, 3, 2) |
| 4 | (1, 3, 3) | (1, 3, 1), (1, 3, 3), (1, 2, 3), (2, 3, 3) |
| 5 | (3, 1, 3) | (3, 1, 1), (3, 1, 3), (3, 2, 3), (2, 1, 3) |
Spätestens nach diesen fünf Versuchen ist das Schloss offen, denn in der letzten Spalte der Tabelle kommen alle 27 Möglichkeiten vor.
Wie man auf die Tabellenlösung kommt? Eine Möglichkeit besteht darin, sich jeden Code als Punkt in einem 3×3×3-Würfel vorzustellen. Dann schließt jeder Code gerade die Punkte im Würfel aus, die auf einer gemeinsamen achsenparallelen Geraden mit diesem Code liegen.
In obigem Bildchen sind die fünf Codes der Tabelle durch große Punkte markiert. Man erkennt, dass jeder andere Punkt auf einer gemeinsamen achsenparallelen Geraden mit irgendeinem der fünf markierten Punkte liegt. Um solche fünf Punkte zu finden, muss man aber trotzdem noch ein wenig probieren. (Insbesondere wird man, wie zuvor bewiesen, mit vier Punkten nicht auskommen!)
Aufgabe 4
Man nehme den Prospekt eines beliebigen Supermarktes, Möbelhauses oder
Computerladens. Jedes Produkt hat dort seinen Preis - und um diese Preise soll
es in dieser Aufgabe zunächst einmal gehen.
Schaut man sich diese Zahlen nämlich genauer an, so stellt man in der Regel
fest: Die meisten Preise haben als letzte Ziffer eine 9, einige wenige vielleicht
eine 0 oder 5, aber andere Ziffern kommen so gut wie gar nicht vor.
Doch in dieser Aufgabe soll nicht die letzte, sondern die erste Ziffer
der Zahlen eine Rolle spielen. Uns interessiert folgende Frage:
Kommen die Zahlen 1, 2, 3, 4, 5, 6, 7, 8 und 9 gleich oft als erste Ziffer vor oder nicht?
janein
Für die letzte Ziffer haben wir die Frage oben beantwortet, da kommt die 9
eindeutig häufiger vor. Bevor du auf der Rückseite weiterliest, solltest du
jetzt erst einmal versuchen, eine Antwort auf obige Frage zu finden.
Hast du eine Vermutung aufgestellt? Dann solltest du sie überprüfen! Fertige
dir dazu eine Tabelle (zum Beispiel) nach folgendem Muster an:
| Preise mit 1. Ziffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Gesamtzahl |
| ALBI-Prospekt | 71 | 61 | 40 | 31 | 20 | 16 | 18 | 13 | 18 | 288 |
| in Prozent | 24,6 | 21,2 | 13,9 | 10,7 | 6,9 | 5,5 | 6,3 | 4,6 | 6,3 | 100 |
| Opi-Baumarkt | &vellip#vdots; | |||||||||
| &vellip#vdots; | ||||||||||
- Nullen am Anfang zählen nicht. Das heißt z. B., die erste Ziffer von 0,49 DM ist eine 4.
- Die Anzahl der gezählten Preise muss möglichst groß sein, also etwa zwischen 250 und 1000 liegen. Das geht mit einer Strichliste ziemlich schnell.
- Welche Beobachtungen hast du gemacht (Tabelle !)?
- Stelle die Tabellenwerte grafisch dar! Trage auf der x-Achse die Ziffern (1, 2, ...9), auf der y-Achse die zugehörigen prozentualen Häufigkeiten auf.
- Gibt es eine Gesetzmäßigkeit? Kennst du eine Funktion, mit der man die Punkte der Graphen verbinden kann?
- Warum treten die Zahlen in der Umwelt so auf, wie du es beobachtet hast? (Man kann das mathematisch begründen.)
Lösung:
Zunächst einmal eine kleine Geschichte: Am Anfang des zwanzigsten
Jahrhunderts gab es noch keine Taschenrechner oder Computer, mit denen
Wissenschaftler ihre Berechnungen durchführen konnten. Stattdessen
bediente man sich sogenannter Logarithmentafeln; vielleicht habt
ihr so etwas schon mal in älteren Formelsammlungen gesehen. Mit diesen konnte
man dann auch kompliziertere Berechnungen vereinfachen.
Man muss sich das als Buch vorstellen, in dem in einer großen Tabelle für
sehr viele Zahlen
zwischen 1 und 10 (also z. B. in 1/10000-Schritten) der Logarithmus dieser
Zahlen angegeben war, also die Zahl, die man heute beim Taschenrechner durch
einfaches Drücken der log-Taste erhält. Wenn ihr das mal ausprobiert,
werdet ihr feststellen, dass diese Tabelle ausreicht, um den
Logarithmus von allen Zahlen mit einer bestimmten Genauigkeit zu
ermitteln (Vergleicht einfach mal die Werte von log 1, 2, log 12
und log 120!).
Ein amerikanischer Physiker namens Frank Benford, der sein
Logarithmentafelbuch sehr oft benutzt haben muss, stellte 1938 fest,
dass die vorderen Seiten viel mehr abgegriffen waren als die
hinteren. In seinen Berechnungen mussten also sehr viel häufiger
Zahlen vorgekommen sein, die mit einer 1 oder 2 angefangen haben, als
solche, die mit einer 8 oder 9 beginnen. Diese Feststellung wurde
später nach ihm ,,Benfords Gesetz`` oder auch ,,First-Digit-Gesetz`` genannt, obwohl sie auch
schon 1881 von Simon Newcomb gefunden wurde:
Die Wahrscheinlichkeit, dass eine Zahl mit 1 beginnt, ist viel größer (ca. 30 Prozent) als die Wahrscheinlichkeit, dass eine Zahl mit 9 beginnt (ca. 5 Prozent). Genauer gesagt ist die Wahrscheinlichkeit, dass eine Zahl mit der Ziffer n beginnt, log() (siehe Schaubild
).
![\includegraphics[]{benford.eps}](img17.png)
Kann man dieses ,,Gesetz`` irgendwie begründen?
Die wichtigste Feststellung ist, dass die meisten Vorgänge weniger in
absoluten Zahlen als vielmehr in Größenordnungen einzuordnen sind. Es
gibt viel mehr Pfützen als Tümpel, mehr Tümpel als Seen und mehr
Seen als Meere. Wenn man also die Flächen der Gewässer betrachtet, so
gibt es mehr zwischen einem und zwei Quadratmetern als zwischen zwei
und drei Quadratmetern, ebenso zwischen 100 000 Quadratmetern und 200 000 Quadratmetern mehr als
zwischen 200 000 und 300 000.
Doch man kann noch genauer analysieren: Die Anzahl der Gewässer mit
Größe zum Beispiel zwischen einem und zwei Quadratmetern ist gleich der Anzahl
der Gewässer mit Größen zwischen zwei und vier Quadratmetern und
der Anzahl mit Größen zwischen vier und acht Quadratmetern. Dies ist
die Voraussetzung dafür, dass die Verteilung der Anfangsziffern so
aussieht wie im Schaubild angegeben. Denn dann ist der Balken bei der
Eins gerade so groß wie die von Zwei und Drei zusammen und so groß
wie die von Vier, Fünf, Sechs und Sieben zusammen. Man nennt diese Eigenschaft
,,Skaleninvarianz``.
Solche Verteilungen findet man insbesondere bei exponentiellen
Wachstumsvorgängen, was nichts anderes bedeutet, als dass sich eine
bestimmte Größe in einem gewissen Zeitintervall (zum Beispiel ein Jahr)
jeweils vervielfacht (also zum Beispiel verdoppelt, verdreifacht,
halbiert). So etwas findet man in der Umgebung sehr häufig, auf der
einen Seite bei Populationen von Bakterien, auf der anderen Seite bei
Sparguthaben oder Aktienindizes. Das Erstaunliche ist, dass dieses
Gesetz auch bei Größen gilt, für die diese Art von Wachstum nicht so offensichtlich
auftritt, zum Beispiel bei Dateigrößen auf einer Festplatte oder beliebig
ausgewählten Zahlen in einer Zeitung. Es scheint sich also um eine
Verteilung der Verteilungen zu handeln!
Und wer die Dateigrößen auf seiner Festplatte untersucht hat, wird
festgestellt haben, dass diese bei genügend großer Anzahl gut dem
Gesetz gehorchen, die Abweichung beträgt meist nur ein paar
Prozent. Aber man stellt auch meistens bei der einen oder anderen Zahl
einen ,,Ausreißer`` fest. Und solche Ausreißer deuten darauf
hin, dass auf dieser Festplatte nicht nur irgendwelche Daten liegen,
sondern eine größere Anzahl einer ganz bestimmten Sorte, zum Beispiel Abspeicherungen
eines Programms.
Damit hat das Verfahren auch eine praktische Bedeutung: In den USA
untersucht man Steuererklärungen großer Unternehmen, indem man die
Häufigkeit der Anfangsziffern zählt.
(maschinell, sind ja keine Lochkarten, die Genauigkeit ist also recht hoch).
Genügen sie Benfords Gesetz, scheint alles in Ordnung. Hat aber jemand die
Bilanzen gefälscht, so weicht die Verteilung ab, da die
meisten Menschen dazu tendieren, eher Zahlen, die mit 5 oder 6 beginnen,
auszuwählen und damit Benfords Gesetz zu verletzen.
Auch bei den von euch untersuchten Supermarktpreisen kann man diese
Gesetzmäßigkeit feststellen:
![\includegraphics[]{super.eps}](img18.png)
Der Verlauf der Kurve entspricht für die Anfangsziffern 1 bis 8 Benfords
Gesetz. Andererseits sieht man deutlich, dass viel mehr Preise, als man nach
diesem Gesetz erwarten würde, mit einer 9 beginnen, vermutlich aus
psychologischen Gründen.
Viel mehr zu diesem Thema findet man im Internet, zum Beispiel unter
- http://www.zmija.de/ziffernanalyse.htm und
- www.math.uni-augsburg.de/stochastik/drton/Firstdigit/
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File

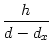 ,
,
![\includegraphics[width=7.0cm]{git.eps}](img15.png)