a)
In dem ,,Buch der Wahrheit`` stehen merkwürdige Dinge:
Auf der ersten Seite steht: ,,In diesem Buch steht genau eine falsche
Aussage.``
Auf der zweiten Seite steht: ,,In diesem Buch stehen genau zwei falsche
Aussagen.``
Und so weiter, bis schließlich auf Seite 2002, der letzten Seite, steht:
,,In diesem Buch stehen genau 2002 falsche Aussagen.``
Wie viele falsche Aussagen stehen tatsächlich in diesem Buch, und wo stehen
sie gegebenenfalls?
b)
Das ,,Buch der Lügen`` ist etwas allgemeiner gefasst:
Auf der ersten Seite steht: ,,In diesem Buch steht mindestens eine falsche
Aussage.``
Auf der zweiten Seite steht: ,,In diesem Buch stehen mindestens zwei
falsche Aussagen.``
Und so weiter, bis schließlich auf Seite 2002, ebenfalls der letzten Seite,
steht:
,,In diesem Buch stehen mindestens 2002 falsche Aussagen.``
Wie viele falsche Aussagen stehen nun in diesem Buch, und wo stehen
sie gegebenenfalls?
Lösung:
a) Können im ,,Buch der Wahrheit`` zwei oder mehr richtige
Aussagen stehen?
Das würde dann bedeuten, dass sowohl eine Aussage ,,In diesem Buch
stehen genau x falsche Aussagen`` als auch eine andere Aussage
,,In diesem Buch stehen genau y falsche Aussagen`` gleichzeitig
wahr sein müssten. Das ist aber wegen des Wörtchens ,,genau`` ein
Widerspruch.
Ist andererseits überhaupt keine Aussage im Buch wahr, dann
müssten
alle 2002 Aussagen falsch sein. Dann wäre aber doch eine
Aussage wahr,
nämlich die auf Seite 2002, also führt dies ebenfalls zum Widerspruch.
Es verbleibt als letzte und einzige Möglichkeit, dass genau eine
Aussage wahr ist, und die anderen 2001 falsch. Dies führt zu keinem
Widerspruch: Die wahre Aussage ist
die auf Seite 2001, alle anderen 2001 Aussagen sind falsch.
b) Hier kommt es auf das Wörtchen ,,mindestens`` an. Wenn die Aussage auf einer bestimmten Seite richtig ist (z. B. Seite 10), dann sind die Aussagen auf allen vorhergehenden Seiten ebenfalls korrekt (in diesem Fall dann die Seiten 1 bis 9). Es gibt also in diesem Buch höchstens eine ,,magische`` Seite: Die Aussagen auf allen Seiten davor und auf der Seite selbst sind richtig, alle Aussagen danach sind falsch. Die Seitennummer dieser magischen Seite entspricht somit der Anzahl der auf diese Seite folgenden Seiten des Buches, diese Seitennummer ist also gerade die Hälfte der Gesamtseitenzahl. Folglich hat die magische Seite die Seitennummer 1001. Genau 1001 Aussagen des Buches sind falsch, dies sind alle Aussagen der folgenden 1001 Seiten. Die Aussagen der ersten 1001 Seiten sind somit alle wahr.
Bemerkung:
Es kann korrekt nur von höchstens einer magischen Seite gesprochen
werden, weil die Aufgabe für ein Buch mit ungerader Seitenzahl unlösbar ist:
Die Aussage auf der mittleren Seite kann weder wahr noch falsch sein.
Aufgabe 2
Wie viele Möglichkeiten gibt es, vier Türme so auf ein Schachbrett zu
stellen, dass keiner einen anderen bedroht?
Lösung:
Zwei Türme bedrohen sich bekanntlich genau dann, wenn sie in einer gemeinsamen
Zeile oder einer gemeinsamen Spalte des Schachbrettes stehen.
Um vier Türme ohne gegenseitige Bedrohung zu platzieren, muss man also
zunächst vier verschiedene Zeilen und unabhängig davon vier verschiedene
Spalten aus den jeweils acht zur Verfügung stehenden auswählen. Hierfür hat
man je
![]() Möglichkeiten1.
Möglichkeiten1.
Schließlich darf man in jeder der vier ausgewählten Zeilen die Spalte
wählen, in die der Turm soll. Für die erste Zeile hat man vier Spalten zur
Verfügung, für die zweite nur noch drei, für die dritte noch zwei und die
letzte Spalte steht dann fest. Das sind noch einmal
4 . 3 . 2 . 1
Möglichkeiten, die Türme in die gewählten Zeilen und Spalten zu stellen.
Insgesamt ergeben sich also
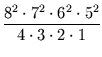 = 117600 = 117600 |
Möglichkeiten.
Alternativ kann man auch so zählen: für den ersten Turm hat man 64
mögliche Felder. Da er genau 15 Felder bedroht (inklusive dem eigenen)
bleiben für den zweiten Turm noch 49 mögliche Felder. Der zweite Turm
bedroht genau 13 weitere Felder, so dass man für den dritten Turm noch 36
Felder zur Verfügung hat und schließlich für den letzten Turm noch 25.
Da es auf die Reihenfolge der Türme nicht ankommt, erhält man jede Stellung
hierbei
4 . 3 . 2 . 1 mal, so dass sich auch hier wieder 117600
Möglichkeiten ergeben.
Aufgabe 3
Um ein konvexes Polygon, das einen Umfang U hat, wird ein Rahmen
gezeichnet, dessen Außenlinien in einem Abstand b parallel zu den
Polygonseiten verlaufen (vgl. Zeichnung).
Beweise, dass die Fläche des Rahmens größer als
b(U + ![]() b) ist.
b) ist.
![\includegraphics[width=5cm]{polygon.eps}](img12.png)
Hinweis: Ein konvexes Polygon ist ein Vieleck, in dem alle Innenwinkel kleiner als 180o sind.
Lösung:
![\includegraphics[width=5cm]{polygonloes.eps}](img13.png)
Um die Fläche des Rahmens abzuschätzen, werden zuerst die Senkrechten zu den
Polygonseiten durch die Eckpunkte des Polygons gezeichnet (vgl. Skizze).
Dadurch wird der Rahmen in Rechtecke und kleine Eckstücke zerlegt. Die
Rechtecke überschneiden sich nicht, weil das Polygon konvex ist; sie haben
alle eine Breite von b und die Summe der Längen der
Rechtecke ist gerade der Umfang U des Polygons, weshalb sie
zusammen einen Flächeninhalt von b . U haben.
Nun sind noch die kleinen Eckstücke zu betrachten. In den Rahmen lassen sich
Kreisbögen mit Radius b einbeschreiben. Die Winkel der entstehenden
Kreissegmente addieren sich gerade zu
360o, weshalb die Summe der
Flächen der Eckstücke größer ist als eine Kreisfläche mit Radius b,
d. h. größer als
![]() . b2.
. b2.
Die Rahmenfläche ist also größer als
b . U + ![]() . b2 = b(U +
. b2 = b(U + ![]() b).
b).
Aufgabe 4
Asterix und Obelix spielen ein Spiel. Dabei werfen sie eine
Münze und schreiben auf, in welcher Reihenfolge Adler (A) oder Zahl (Z)
oben liegen. Jeder hat sich eine Dreierfolge ausgesucht, und das Spiel wird
beendet, sobald in der (bis dahin evtl. recht langen) Folge der Ergebnisse eine
der beiden Dreierfolgen auftaucht. Es gewinnt natürlich, wessen Folge
erschienen ist.
- a)
- Man hätte zunächst denken mögen, dass keiner der beiden einen
Vorteil hat, weil ja jede Dreierfolge mit gleicher Wahrscheinlichkeit einmal
geworfen wird. Warum kann man dieses Argument hier eigentlich nicht anwenden?
- b)
- Auf dem letzten Zettel wurde errechnet, dass ZAA gegen AAZ mit 3/4 zu 1/4 und AAZ gegen AZA mit 2/3 zu 1/3 gewinnt. Gewinnt deswegen dann auch im Mittel ZAA gegen AZA?
Lösung:
Zu a): Das Argument ist deswegen nicht anwendbar, weil die Bedingungen, unter
denen mit dem Werfen der Münze aufgehört wird, mit dem Auftreten der Tripel
zusammenhängen. Würden immer gleich lange Ketten geworfen werden (oder auch
mit einer jedesmal von den Würfen unabhängig per Zufall bestimmten Länge)
und dann gezählt, wie oft welche Kombination gekommen ist, hätte keiner einen
Vorteil. Bei diesem Spiel ist es aber von Bedeutung, dass es z. B. bei der
Paarung AAZ gegen ZAA sehr wahrscheinlich ist, dass vor dem Auftreten
eines Tripels AAZ ein Tripel ZAA kam. Die einzige Ausnahme (und damit
einzige Chance für Asterix) ist der Fall, dass gleich zu Anfang mindestens
zwei A geworfen werden.
,,Ja, aber, ... heißt das dann nicht, dass irgendwie ZAA im
Mittel früher geworfen wird als AAZ¿` Das stünde in der Tat im
Widerspruch zu der Tatsache, dass ohne wurfabhängige Abbruchbedingung alle
Tripel gleich oft vorkommen. Aber die vermeintliche Folgerung ist auch direkter
zu entkräften: Zwar kommen nach Werfen des ersten Z die Tripel ZAA und
AAZ immer paarweise vor, wobei ZAA vorangeht. Aber es kann ja gleich zu
Anfang
A...AZ geworfen worden sein. Dann kommt immer AAZ zuerst. Dies
geschieht zwar nur mit der Wahrscheinlichkeit 1/4. Aber wenn ein AAZ kommt,
kann das nächste ZAA frühestens zwei Stellen später vorkommen, während
nach einem ZAA das nächste AAZ direkt folgen kann (und sozusagen ,,
zwingend``, nämlich nach Ende der A-Kette erscheint). Dadurch wird der
scheinbare Vorteil von ZAA wieder ausgeglichen.
Zu b): So einfach kann man leider auch nicht schließen. (Der Mathematiker
sagt: Die Relation ,,siegt gegen`` ist nicht transitiv.) In der
Tat sind ZAA und AZA gegeneinander gleichwertig:
Sei xA die Gewinnwahrscheinlichkeit für AZA in dem Fall, dass als Erstes
ein A geworfen wurde; xZ diejenige für den Fall, dass als Erstes ein Z
geworfen wurde.
Sei zunächst ein A geworfen worden. Fällt ein weiteres A, ist das erste
A für beide Spieler wertlos und die
Situation so, als ob nur ein A liegen würde. Fällt stattdessen ZA, so hat
AZA gewonnen. Fällt ZZ, so ist die Situation so, als ob nur ein Z
geworfen worden wäre. Also gilt:
| xZ | = | 1/4 . 0 + 1/8 + 1/8xZ + 1/2xZ | |
| = | 1/3. |
Weiterhin folgt daraus
| xA | = | 2 . (1/4 + 1/4 . 1/3) = 2/3 und | |
| x | = | 1/2xA + 1/2xZ = 1/2 |
für die Wahrscheinlichkeit, dass AZA gewinnt. Mithin gewinnt ZAA mit der gleichen Wahrscheinlichkeit.
Bemerkung:
Das Phänomen der Intransitivität ist übrigens weniger verwunderlich, als es
auf den ersten Blick erscheinen mag: Wenn im
Sport meistens A gegen B und B gegen C gewinnt, heißt das ja noch
nicht, daß meistens auch A gegen C gewinnt. Die Taktik von A kann ja so
sein, daß sie C nicht beeindruckt. Ein konkretes Beispiel nannte ein
Teilnehmer: Beim Spiel ,,Schere, Stein, Papier`` wird ,,im Kreis``
gewonnen.
Auch beim Spiel von Asterix und Obelix gibt es so eine Folge (übrigens nur genau diese eine): Es gewinnen
- ZAA gegen AAZ mit 3/4 zu 1/4,
- AAZ gegen AZZ mit 2/3 zu 1/3,
- AZZ gegen ZZA mit 3/4 zu 1/4,
- ZZA gegen ZAA mit 2/3 zu 1/3.
Das Spiel bietet noch weiteren Stoff für interessante Entdeckungen. Wenn acht Leute mit allen acht verschiedenen Tripeln mitspielen, ist es wieder ein faires Spiel, denn es wird jedesmal nach drei Würfen geendet. Was passiert jedoch ,,auf dem Weg dahin``, d. h. wenn man nach und nach die Spieleranzahl erhöht? Müssen sich die Verhältnisse immer weiter angleichen? Das ist nicht der Fall. Ein Beispiel: ZAZ gewinnt gegen AAA mit 4/7 zu 3/7. Wenn nun zu dritt mit ZAA gespielt wird (das gegen ZAZ neutral spielt und gegen AAA mit 7/8 zu 1/8 gewinnt), so ist das Gewinnverhältnis: ZAZ : AAA : ZAA = 7/16 : 1/8 : 7/16. Im direkten Vergleich zwischen ZAZ und AAA steht es jetzt also haushohe 7/16 zu 2/16 !
Fußnoten
- ... M"oglichkeiten1
- Allgemein geben die sogenannten Binomialkoeffizienten
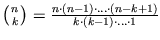 gerade die Anzahl der
Möglichkeiten, k Elemente aus einer n-elementigen Menge auszuwählen,
an. Siehe dazu auch die Erklärungen auf dem Aufgabenblatt 9 zur ,,
Zwergenaufgabe``.
gerade die Anzahl der
Möglichkeiten, k Elemente aus einer n-elementigen Menge auszuwählen,
an. Siehe dazu auch die Erklärungen auf dem Aufgabenblatt 9 zur ,,
Zwergenaufgabe``.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
