Beispiellösungen zu Aufgabenblatt 27

aktualisiert: 1. Juli 2003

Aufgabe 1


Welche reellen Zahlen x erfüllen die Gleichung

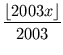$\displaystyle \left\lfloor\vphantom{ \frac{\lfloor 2003 x\rfloor}{2003}}\right.$$\displaystyle {\frac{{\lfloor 2003 x\rfloor}}{{2003}}}$$\displaystyle \left.\vphantom{ \frac{\lfloor 2003 x\rfloor}{2003}}\right\rfloor$ = 2003?    


Dabei ist $ \lfloor$ $ \rfloor$ die Gaußklammer, das heißt: $ \lfloor$x$ \rfloor$ bezeichnet die größte ganze Zahl, die nicht größer als x ist. Es gilt also x - 1 < $ \lfloor$x$ \rfloor$ $ \leq$ x.


Lösung:


Die Ungleichungskette x - 1 < $ \lfloor$x$ \rfloor$ $ \leq$ x lässt sich in die beiden Ungleichungen x - 1 < $ \lfloor$x$ \rfloor$     $ \Leftrightarrow$     x < $ \lfloor$x$ \rfloor$ + 1 und $ \lfloor$x$ \rfloor$ $ \leq$ x zerlegen, die man äquivalent zu der Kette $ \lfloor$x$ \rfloor$ $ \leq$ x < $ \lfloor$x$ \rfloor$ + 1 zusammensetzen kann.

Ersetzt man zunächst den Gaußklammernausdruck durch eine ganze Zahl n, wird es vielleicht klarer: Eine ganze Zahl n ist genau dann die Gaußklammer $ \lfloor$z$ \rfloor$ einer reellen Zahl z, wenn gilt: z - 1 < n $ \leq$ z bzw. äquivalent n $ \leq$ z < n + 1.

Hier ist $ \lfloor$z$ \rfloor$ = 2003 vorgegeben (mit z = $ {\frac{{\lfloor 2003 x\rfloor}}{{2003}}}$); also gelten folgende Äquivalenzen:

      $\displaystyle \left\lfloor\vphantom{ \frac{\lfloor 2003 x\rfloor}{2003}}\right.$$\displaystyle {\frac{{\lfloor 2003 x\rfloor}}{{2003}}}$$\displaystyle \left.\vphantom{ \frac{\lfloor 2003 x\rfloor}{2003}}\right\rfloor$ = 2003    
$\displaystyle \Longleftrightarrow$ 2003 $\displaystyle \leq$ $\displaystyle {\frac{{\lfloor 2003 x\rfloor}}{{2003}}}$ < 2004
$\displaystyle \Longleftrightarrow$ 2003 . 2003 $\displaystyle \leq$ $\displaystyle \lfloor$2003x$\displaystyle \rfloor$ < 2003 . 2004
$\displaystyle \Longleftrightarrow$ 2003 . 2003 $\displaystyle \leq$ 2003x < 2003 . 2004
$\displaystyle \Longleftrightarrow$ 2003 $\displaystyle \leq$ x < 2004
   

Die Gleichung ist also genau für die reellen Zahlen x mit 2003 $ \leq$ x < 2004 erfüllt.


Aufgabe 2


Von beliebigen fünf Stäben wird lediglich vorausgesetzt, dass man jeweils drei von ihnen zu einem Dreieck zusammenlegen kann. Es ist nachzuweisen, dass mindestens eines der Dreiecke spitzwinklig ist.


Lösung:


Wir benötigen folgende Aussage:

Gegeben sei ein Dreieck mit den Seitenlängen a $ \leq$ b $ \leq$ c. Dann ist das Dreieck genau dann spitzwinklig, wenn a2 + b2 > c2 ist.

Diese Aussage kann man sich relativ leicht herleiten. Zunächst eine Herleitung ,,zu Fuß``: Wenn man zwei Seitenlängen a und b gegeben hat, kann man die Seiten natürlich im rechten Winkel zusammenlegen und mit einer Seite der Länge c mit c2 = a2 + b2 zu einem rechtwinkligen Dreieck ergänzen. Ein kleinerer Winkel erfordert eine kürzere dritte Seite, ein größerer entsprechend eine längere. Mit a2 + b2 > c2 ist also zumindest derjenige Winkel spitz, der der Seite c gegenüber liegt. Die Ungleichungen a2 + c2 > b2 und b2 + c2 > a2 gelten aber ohnehin wegen der Voraussetzung a $ \leq$ b $ \leq$ c, womit die beiden anderen Winkel in jedem Fall spitz sind.

Kürzer ist die Herleitung, wenn man z. B. den Kosinussatz heranzieht; dieser besagt ja, dass gilt: c2 = a2 + b2 - 2ab cos$ \gamma$; dabei ist $ \gamma$ der Winkel, der der Seite c gegenüber liegt. Und der Kosinus ist genau dann größer als null, wenn $ \gamma$ < 90o gilt.


Nun sei angenommen, es gebe fünf Stäbe mit den Längen a $ \leq$ b $ \leq$ c $ \leq$ d $ \leq$ e, von denen man keine drei zu einem spitzwinkligen Dreieck zusammenlegen kann. Dann gelten die Ungleichungen

a2 + b2 $\displaystyle \leq$ c2,  
b2 + c2 $\displaystyle \leq$ d2    und  
c2 + d2 $\displaystyle \leq$ e2.  

Zusammengenommen ergibt sich die Ungleichungskette

a2 + b2 $\displaystyle \leq$ c2 $\displaystyle \leq$ d2 - b2 $\displaystyle \leq$ e2 - c2 - b2 $\displaystyle \leq$ e2 - 2ab,

da ja außerdem a $ \leq$ b $ \leq$ c gelten sollte.

Daraus folgt aber insbesondere

(a + b)2 $\displaystyle \leq$ e2,

und dies steht im Widerspruch dazu, dass man aus den Stäben mit den Längen a, b und e ein Dreieck legen können soll, denn dies geht nur, wenn a + b > e ist.


Aufgabe 3


Ein getöntes Fenster der Firma ,,Glasoflex`` besteht aus drei parallelen Scheiben im Abstand von wenigen Zentimetern. Jede der Scheiben lässt 70 Prozent des auf sie fallenden Lichtes durch (egal, von welcher Seite das Licht auf die Scheibe fällt), reflektiert 20 Prozent und die restlichen 10 Prozent werden absorbiert (bleiben in der Scheibe).
Wie viel Prozent des einfallenden Lichtes werden von einem Fenster der Firma Glasoflex durchgelassen?



Beachte, dass zum Beispiel der Teil des Lichtes, der von der zweiten Scheibe reflektiert wird, wieder auf die erste Scheibe fällt und dort zum Teil wieder reflektiert wird usw.


Lösung:


Der Weg der Lichtstrahlen durch ein Fenster von Glasoflex:


\includegraphics[]{glas00.eps}


Lösungsvariante A:


In dieser Lösung betrachten wir zuerst, wie viel Licht durch zwei Scheiben hindurchgeht und wie viel Licht an zwei Scheiben insgesamt gespiegelt wird. Diese Daten nutzen wir anschließend um auszurechen, wie viel Licht durch drei Scheiben hindurchfällt.


Eine Scheibe:

\includegraphics[]{glask1.eps}
Die Angaben für eine Scheibe entnehmen wir der Aufgabenstellung. Durch eine Scheibe geht d1 = 0, 7 (=70%) des einfallenden Lichtes (statt mit Prozent rechnen wir mit Dezimalzahlen (von 0 bis 1)) und s1 = 0, 2 wird gespiegelt (dass der Rest absorbiert wird, wird hier nicht weiter benötigt).


Zwei Scheiben:

\includegraphics[]{glask2.eps}

Sei t2 der Anteil des vor der zweiten Scheibe ankommenden Lichtes, der insgesamt durch diese Scheibe geht (unter Berücksichtigung, dass davor eine erste Scheibe steht). Dann gilt

t2 = 0, 7 + 0, 2 . 0, 2 . t2,

denn der 0, 7-fache Teil geht sofort durch die zweite Scheibe hindurch und zusätzlich wird der 0, 2-fache Teil an der zweiten Scheibe gespiegelt, davon wird der 0, 2-fache Teil an der (Rückseite der) ersten Scheibe gespiegelt, und für das nun an die Scheibe ankommende Licht ist genau t2 der Faktor, der beschreibt, welcher Anteil hiervon durch die Scheibe fällt (direkt und nach weiteren Spiegelvorgängen). Also gilt

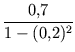t2 = $\displaystyle {\frac{{0,7}}{{1-(0,2)^2}}}$ = $\displaystyle {\frac{{70}}{{96}}}$.

Da vor der zweiten Scheibe bereits die erste Scheibe nur 70% des Lichtes durchlässt, gilt für den Faktor d2, der beschreibt, wie viel Licht durch zwei Scheiben insgesamt hindurchkommt:

d2 = 0, 7 . t2 = $\displaystyle {\frac{{7^2}}{{96}}}$ = $\displaystyle {\frac{{49}}{{96}}}$.


Außerdem brauchen wir noch den Anteil s2 an Licht, der insgesamt von zwei Scheiben gespiegelt wird. Dieser berechnet sich als

s2 = 0, 2 + 0, 7 . 0, 2 . t2,

denn der 0, 2-fache Teil des ankommenden Lichtes wird sofort an der ersten Scheibe gespiegelt. Zusätzlich fällt der 0, 7-fache Teil durch die erste Scheibe hindurch, davon wird der 0, 2-fache Teil an der zweiten Scheibe gespiegelt und von diesem (von innen) vor der ersten Scheibe eintreffenden Licht kommt genau der t2-fache Teil wieder durch die erste Scheibe. Also gilt

s2 = 0, 2 + 0, 7 . 0, 2 . $\displaystyle {\frac{{70}}{{96}}}$ = $\displaystyle {\frac{{29}}{{96}}}$.


Drei Scheiben:

\includegraphics[]{glask3.eps}

Sei t3 der Anteil des vor der dritten Scheibe ankommenden Lichtes, der insgesamt durch diese dritte Scheibe geht (unter Berücksichtigung, dass davor noch zwei Scheiben stehen). Dann gilt

t3 = 0, 7 + 0, 2 . s2 . t3,

denn der 0, 7-fache Teil geht sofort durch die dritte Scheibe hindurch; zusätzlich wird der 0, 2-fache Teil an der dritten Scheibe gespiegelt, davon wird der s2-fache Teil von den ersten beiden Scheiben zusammen zurückgespiegelt, und dann beschreibt wieder genau der Faktor t3, wie viel Licht hiervon insgesamt noch durch die dritte Scheibe hindurchgelassen wird.

Also gilt

t3 = 0, 7 . $\displaystyle \left(\vphantom{1-0,2\cdot\frac{29}{96}}\right.$1 - 0, 2 . $\displaystyle {\frac{{29}}{{96}}}$$\displaystyle \left.\vphantom{1-0,2\cdot\frac{29}{96}}\right)^{{-1}}_{}$ = $\displaystyle {\frac{{7}}{{10}}}$ . $\displaystyle {\frac{{960}}{{902}}}$.

Da vor der dritten Scheibe die ersten beiden Scheiben nur den d2-fachen Anteil des Lichtes durchfallen lassen, gilt für den Faktor d3, der beschreibt, wie viel Licht durch drei Scheiben insgesamt hindurchkommt:

d3 = d2 . t3 = $\displaystyle {\frac{{7^2}}{{96}}}$ . $\displaystyle {\frac{{7}}{{10}}}$ . $\displaystyle {\frac{{960}}{{902}}}$ = $\displaystyle {\frac{{7^3}}{{902}}}$ = $\displaystyle {\frac{{343}}{{902}}}$.


Also fallen insgesamt $ {\frac{{34300}}{{902}}}$% $ \approx$ 38% des einfallendes Lichtes durch ein aus drei Scheiben bestehendes Fenster der Firma Glasoflex.


Lösungsvariante B:


Hier betrachten wir zusammenfassend, wie viel Licht in welchem Abschnitt in welcher Richtung strahlt - vgl. Abbildung: die den Pfeilen zugeordneten Variablen stehen jeweils für den Anteil am eingestrahlten Licht. Das Licht kommt von der linken Seite auf das Fenster (voller Anteil, daher a = 1). (Der Teil des Lichtes, der nach links wieder wegstrahlt, ist hier nicht von Interesse und wird daher nicht betrachtet.) Zwischen der ersten und der zweiten Scheibe gehen Lichtstrahlen in beide Richtungen, genauso zwischen der zweiten und der dritten. Auf der anderen Seite strahlt nur Licht heraus.


\includegraphics[width=9cm]{glas11.eps}

Nun betrachten wir, woher das jeweilige Licht kommt, und erhalten ein lineares Gleichungssystem in den Variablen b, c, d, e und f. Die Lösung der Aufgabe ist der Wert von f.

Licht zum Pfeil b kommt entweder direkt von draußen durch die erste Scheibe durch - also 70 % davon bzw. 0, 7 (wir rechnen wieder mit Dezimalzahlen statt mit Prozent) - oder es ist aus Richtung c an der ersten Scheibe gespiegelt. Das ergibt:

b = 0, 7 . 1 + 0, 2 . c. (1)

Und entsprechend ergeben sich die Gleichungen für die anderen Variablen:
c = 0, 2 . b + 0, 7 . e (2)
d = 0, 7 . b + 0, 2 . e (3)
e = 0, 2 . d (4)
f = 0, 7 . d (5)

Einsetzen von (4) in (3) ergibt
d = 0, 7 . b + 0, 04 . d  
$\displaystyle \Longleftrightarrow$     0, 96 . d = 0, 7 . b  
$\displaystyle \Longleftrightarrow$     b = $\displaystyle {\frac{{96}}{{70}}}$d, (6)

Einsetzen von (4) und (2) in (1) liefert
b = 0, 7 + 0, 2 . c = 0, 7 + 0, 04 . b + 0, 028 . d  
$\displaystyle \Longleftrightarrow$     0, 96 . b = 0, 7 + 0, 028 . d. (7)

Schließlich erhält man aus dem Einsetzen von (6) in (7):
$\displaystyle {\frac{{96^2}}{{7000}}}$d = 0, 7 + 0, 028 . d = 0, 7 + $\displaystyle {\frac{{196}}{{7000}}}$d  
$\displaystyle \Longleftrightarrow$     $\displaystyle {\frac{{9020}}{{7000}}}$d = 0, 7  
$\displaystyle \Longleftrightarrow$     d = $\displaystyle {\frac{{490}}{{902}}}$,  

woraus nach (5)

f = 0, 7 . d = $\displaystyle {\frac{{343}}{{902}}}$ $\displaystyle \approx$ 38%

folgt.

(Eine kleine Testrechnung zeigt, dass zumindest die Tendenz der Lösung richtig ist: Würde kein Licht reflektiert, aber nach wie vor nur 70 % durch eine Scheibe durchgelassen, würden 0, 73 = $ {\frac{{343}}{{1000}}}$ des Lichtes durchkommen. Mit Reflektion muss es mehr sein, was die Rechnung bestätigt.)


Aufgabe 4


Es werden n gewöhnliche Spielwürfel in einer Reihe nebeneinander auf den Tisch gelegt. Man addiert alle Augenzahlen, die nicht durch den Tisch oder durch einen Nachbarwürfel verdeckt sind. Die maximale Augenzahl, die man so erhalten kann, werde mit A(n), die minimale mit a(n) bezeichnet. Wir betrachten nun die Folge der Differenzen d (n) = A(n) - a(n). Für gewisse n ist das Folgenglied d (n) eine Quadratzahl (z. B. für n = 2, n = 6).
Für welche Würfelanzahl n erhält man die 1000. Quadratzahl der Folge?


Lösung:


Bei einem Würfel ist nur die Zahl auf der Tischseite verdeckt. Wir erhalten die maximale Summe an Augenzahlen aller sichtbaren Würfelzahlen, wenn die kleinste Zahl des Würfels - die Eins - verdeckt ist, und entsprechend die minimale Summe, wenn die Sechs verdeckt ist:

A(1) = 21 - 1        und        a(1) = 21 - 6.

Folglich gilt für die Differenz d (1) = 5.

\includegraphics[width=10cm]{wurfel.eps}
Bei zwei oder mehr Würfeln haben wir zwei äußere Würfel, bei denen jeweils die Unterseite und die Seite, die an den Nachbarwürfel grenzt, verdeckt sind, und n - 2 (bei n = 2 Würfeln gibt es davon n - 2 = 0, also keine) innere Würfel. Bei jedem der beiden äußeren Würfel sind mindestens eine Eins und eine Zwei und höchstens eine Sechs und eine Fünf nicht zu sehen. Bei den inneren Würfeln ist die Unterseite (wieder mindestens eine Eins und höchstens eine Sechs) und außerdem noch die zwei Seiten, die jeweils an den Nachbarwürfel grenzen, verdeckt. Da diese beiden Seiten auf dem Würfel einander gegenüber liegen, ist ihre Summe in jedem Fall 7 . Somit erhalten wir

A(n) = n . 21 - [2 . (1 + 2) + (n - 2) . 1 + (n - 2) . 7]

a(n) = n . 21 - [2 . (6 + 5) + (n - 2) . 6 + (n - 2) . 7]

und folglich ist

d (n) = 2 . (11 - 3) + (n - 2)(6 - 1) = 5(n - 2) + 16.


Anzahl an Würfeln ( n ) 1 2 3 4 5 6 7   14 15 16
Differenz ( d (n) ) 5 16 21 26 31 36 41   76 81 86
Quadratzahl ?   ja       ja       ja  

Als Differenzen d (n) erhalten wir die 5 und alle Zahlen, die auf 1 oder 6 enden und größer 15 sind.


Um herauszufinden, welche davon nun Quadratzahlen sind, betrachten wir die Endziffer einer Quadratzahl. Diese hängt nur von der Endziffer der Zahl, die wir quadriert haben, ab:

Endziffer 0 1 2 3 4 5 6 7 8 9
Endziffer des Quadrates 0 1 4 9 6 5 6 9 4 1
Die Quadratzahlen, die unter den Differenzen d (n) auftauchen, sind also

  42, 62, 92,
(10 + 1)2, (10 + 4)2, (10 + 6)2, (10 + 9)2,
(20 + 1)2, (20 + 4)2, (20 + 6)2, (20 + 9)2,
(30 + 1)2, (30 + 4)2, (30 + 6)2, (30 + 9)2,
(40 + 1)2, (40 + 4)2, (40 + 6)2, (40 + 9)2,
(50 + 1)2, (60 + 4)2, (70 + 6)2, (80 + 9)2,
...      

Die k-te Quadratzahl ist das Quadrat von

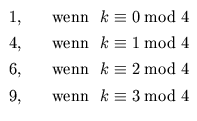
10 . $\displaystyle \left\lfloor\vphantom{\frac{k}{4}}\right.$$\displaystyle {\frac{{k}}{{4}}}$$\displaystyle \left.\vphantom{\frac{k}{4}}\right\rfloor$ + $\displaystyle \left\{\vphantom{\begin{array}{ll} 1 , & \quad\text{wenn }\ k \e... ...2\bmod 4 \\ 9 , & \quad\text{wenn }\ k \equiv 3\bmod 4 \end{array}}\right.$$\displaystyle \begin{array}{ll} 1 , & \quad\text{wenn }\ k \equiv 0\bmod 4 \\ ... ... \equiv 2\bmod 4 \\ 9 , & \quad\text{wenn }\ k \equiv 3\bmod 4 \end{array}$

Für k = 1000 ist dies (10 . 250 + 1)2 = 6.255.001 , als Differenz d (n) ergibt sich diese Zahl nach der Formel 6.255.001 = 5(n - 2) + 16 , also für n - 2 = 1.250.997 .


Somit erhalten wir die 1000. Quadratzahl für n = 1.250.999 Würfel.

drucken Zum Ausdrucken als pdf-File oder als ps-File