Fußball-Superstar Matthias Lothar hat zur Saisonhalbzeit in weniger als
75% aller Spiele ein Tor geschossen, wurde aber in mehr als 75% der
bisherigen Spiele vom Schiedsrichter mit einer gelben Karte verwarnt.
Nach einer kräftigen Standpauke des Trainers verbessert sich Lothar, so dass er am Ende der Saison tatsächlich in mehr als 75% aller Spiele ein Tor geschossen hat und in weniger als 75% der Spiele verwarnt wurde.
Muss es dann notwendigerweise einen Zeitpunkt geben, zu dem Lothar in genau 75% der bisherigen Spiele ein Tor geschossen hat? Muss es einen Zeitpunkt geben, zu dem Lothar in genau 75% der bisherigen Spiele verwarnt wurde?
Anmerkung: Dass in der Bundesliga ein Spieler nach zu vielen gelben Karten gesperrt wird, vernachlässigen wir der Einfachheit halber ...
Lösung:
Es muss tatsächlich einen Zeitpunkt geben, zu dem Lothar in genau 75% der Spiele ein Tor geschossen hat. Denn gäbe es diesen nicht, so müsste er die 75%-Marke in einem Spiel übersprungen haben. Hatte er vor diesem Spiel n Spiele gespielt und in k von diesen ein Tor erzielt, so muss also gelten
Es muss aber keinen Zeitpunkt geben, zu dem er in genau 75% der Spiele
verwarnt wurde. Man betrachte zum Beispiel den Fall, dass
Lothar in jedem Spiel der Hinrunde der Saison, bestehend aus 17 Spielen, verwarnt wurde, dafür aber in keinem der 17 Rückrundenspiele. Nach dem k-ten Spiel der Rückrunde (
0 ![]() k
k ![]() 17) wurde Lothar dann in genau
17) wurde Lothar dann in genau
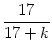 . 100%
. 100%
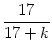 =
=
Aufgabe 2
Fahrraddieb Paul Langfinger hinterließ unvorsichtigerweise mit einem
Beutestück folgende Spur im Schnee:
Dabei stammt eine der beiden Kurven vom Vorderrad, die andere vom Hinterrad.
In welche Richtung sollte man rennen, um Paul eventuell noch einzuholen?
Lösung:
Die Erfahrung lehrt bereits, dass beim Fahrrad das Vorderrad die weiter ausschlagende Spur hinterlässt (was allerdings aus mathematischer Sicht noch unpräzise ist). An Kreuzungspunkten kann man im Schnee zudem vielleicht auch noch sehen, welche der beiden Spuren als zweite entstand - man kann dann davon ausgehen, dass dies die Spur des Hinterrades ist. In beiden Fällen erhält man aber noch keine Aussage über die gefahrene Richtung. Dazu muss man sich die Mechanik des Rades in Bezug auf die Lenkung etwas genauer ansehen. Die (für uns) wichtigsten Beobachtungen sind diejenigen, dass sich der Aufsetzpunkt des Vorderrades beim Lenken (näherungsweise) nicht ändert und dass das Hinterrad nicht lenkbar ist (Ach! ...) - das heißt nämlich, dass es immer in Richtung des Vorderrades zeigt (und rollt), so dass es zu jedem Punkt der Spur des Hinterrades in tangentialer Richtung nach vorne den zugehörigen Punkt des Vorderrades zu finden gibt, und das in immer demselben Abstand. Bei Erwachsenenfahrrädern beträgt dieser Abstand in etwa einen Meter.
Nun schauen wir uns die Spur daraufhin in zwei Bereichen an: Links in der Kurve und in der Nähe des rechten Kreuzungspunktes. Man sieht sehr leicht, dass man an die gestrichelte Kurve keine tangentiale Strecke anlegen kann, die die andere Kurve in sinnvoller Entfernung trifft (jeweils gepunktete Strecken).
![\includegraphics[width=6.1cm]{loes41_2.eps}](img5.png)
Bei der durchgezogenen Kurve gibt es jeweils rechts einen fast geraden Bereich. Es ist nicht möglich, wie beschrieben tangentiale Strecken nach links zu legen, denn die andere Kurve schneidet diese Richtung in recht stumpfem Winkel. Hingegen kann man zu jedem Punkte eine solche tangentiale Strecke nach rechts finden (ein paar sind eingezeichnet), also muss der Fahrraddieb Paul von oben kommend nach rechts gefahren sein, und nach rechts sollte man folglich laufen.
Bemerkung: Eine Feststellung, über die sich vielleicht nachzudenken lohnt: Aufgrund der beschriebenen Eigenschaften ist es aus mathematischer Sicht einfach, zu einer vorgegebenen Bahn des Hinterrades die Spur des Vorderrades zu beschreiben - man gehe einfach immer in der aktuellen Richtung um den Radabstand nach vorne. Andersherum, d. h. wenn man die Spur der Vorderrades gegeben hat - man berechnet dann die so genannte ,,Schleppkurve`` der Spur des Vorderrades - ist das mathematisch ziemlich schwierig und geht meist nur näherungsweise.
In der Praxis dagegen ist es sehr viel einfacher, mit dem Vorderrad eine vorgegebene Spur nachzufahren, als dies mit dem Hinterrad zu tun. Wie kommt das?
Aufgabe 3
Die Mathematiker-Bank bietet ihren Kunden zehnstellige Kontonummern. Nun sind
die meisten Mathematiker recht eigen und wünschen, dass jede Ziffer ihrer
Kontonummer eine Primzahl ist. Danach richtet sich die Bank auch und weiß
zusätzlich
noch, dass Mathematiker bisweilen etwas zerstreut sind und Zahlen verwechseln
- daher sollen sich zwei beliebige Kontonummern in wenigstens fünf Stellen
unterscheiden.
- a).
- Zeige, dass die Bank höchstens 4096 Konten für Mathematiker einrichten kann.
- b).
- Zeige, dass die Bank sogar nur höchstens 2404 Konten bereitstellen kann.
Lösung:
Es gibt genau vier einstellige Primzahlen: 2, 3, 5 und 7. Jede Kontonummer muss also aus diesen Ziffern gebildet werden.
- Keine zwei Kontonummern dürfen in den ersten sechs Stellen übereinstimmen, denn sonst blieben nur noch maximal
die letzten vier Stellen, an denen sie sich unterscheiden könnten. Dies widerspräche der Voraussetzung, dass sich je zwei
beliebige Kontonummern in wenigstens fünf Stellen unterscheiden.
Es gibt aber genau 46 = 4096 verschiedene Möglichkeiten für die ersten sechs Ziffern einer Kontonummer, und da, wie eben gesehen, nur höchstens eine Kontonummer diese ersten sechs Ziffern haben kann, gibt es auch höchstens 4096 verschiedene Kontonummern.
- In der Argumentation bei a) haben wir allerdings noch sehr grob abgeschätzt - schließlich ist überhaupt nicht klar, ob und wie
man jeden dieser 4096 sechsstelligen Kontonummernanfänge zu zehnstelligen Nummern so ergänzen kann, dass wirklich je zwei Ziffern in wenigstens
fünf Stellen unterschiedlich sind.
Dass dies tatsächlich nicht geht, zeigt folgendes Argument:
Angenommen, es gäbe bei der Bank n Kontonummern. Wir schreiben diese in Gedanken nebeneinander in eine lange Reihe. Unter jede der Kontonummern schreiben wir dann in einer Spalte alle jenen zehnstelligen Zahlen bestehend aus den vier erlaubten Ziffern, die sich von der entsprechenden Kontonummer in höchstens zwei Stellen unterscheiden. Das sind in jeder Spalte dann 10 . 3 = 30 Zahlen, die sich an genau einer der zehn Stellen von der gegebenen Kontonummer unterscheiden und
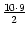 . 32 = 405 Zahlen, die sich an genau zwei Stellen von der gegebenen Kontonummer unterscheiden (für die Wahl dieser beiden
Stellen hat man genau
. 32 = 405 Zahlen, die sich an genau zwei Stellen von der gegebenen Kontonummer unterscheiden (für die Wahl dieser beiden
Stellen hat man genau
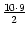 Möglichkeiten).
Zusammen mit der gegebenen Kontonummer selbst stehen in einer Spalte also insgesamt
1 + 30 + 405 = 436 Zahlen. In allen Spalten
zusammengenommen stehen also
n . 436 Zahlen.
Möglichkeiten).
Zusammen mit der gegebenen Kontonummer selbst stehen in einer Spalte also insgesamt
1 + 30 + 405 = 436 Zahlen. In allen Spalten
zusammengenommen stehen also
n . 436 Zahlen.
Diese sind aber alle verschieden! Innerhalb einer Spalte ist dies klar und wären zwei Zahlen aus zwei verschiedenen Spalten gleich, dann würden sich die zu diesen beiden Spalten gehörenden Kontonummern an höchstens 2 + 2 = 4 Stellen unterscheiden - ein Widerspruch.
Also sind die n . 436 Zahlen tatsächlich alle verschieden. Es gibt aber nur genau 410 = 1048576 verschiedene mögliche zehnstellige Zahlen, die man aus den vier Ziffern 2, 3, 5, 7 bilden kann. Daher muss n . 436
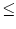 410 gelten und demnach
nDa n ganzzahlig ist, kann es somit höchstens 2404 Kontonummern geben.
410 gelten und demnach
nDa n ganzzahlig ist, kann es somit höchstens 2404 Kontonummern geben.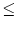
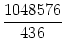 = 2404, 99...
= 2404, 99...
Aufgabe 4
Ein Polynom p(x) habe ganzzahlige Koeffizienten und mindestens sieben
verschiedene ganzzahlige Nullstellen. Zeige, dass dann das Polynom
q(x) = p(x) - 2004 überhaupt keine ganzzahlige Nullstelle hat.
Gilt dies auch noch, wenn p(x) mindestens sechs verschiedene ganzzahlige Nullstellen hat?
Lösung:
Seien a1, a2, a3, a4, a5, a6, a7 sieben verschiedene ganzzahlige Nullstellen von p(x). Da für jede Nullstelle ein Linearfaktor abgespalten werden kann, gibt es ein Polynom r(x) mit ganzzahligen Koeffizienten so, dass
Somit kann man die Zahl 2004 nicht wie gewünscht in ein Produkt zerlegen und es gibt daher keine ganzzahlige Nullstelle a von q(x).
Dies gilt nicht mehr, wenn p(x) nur mindestens sechs verschiedene Nullstellen hat. Man betrachte zum Beispiel
| p(x) | = (x - 1)(x + 1)(x - 2)(x + 2)(x + 3)(x + 167) | |
| = x6 + 170x5 + 496x4 - 850x3 - 2501x2 + 680x + 2004. |
Dieses Polynom hat genau die sechs verschiedenen ganzzahligen Nullstellen 1, - 1, 2, - 2, - 3 und -167; und das Polynom
Der ,,tiefere``Grund dafür, dass die Antwort im zweiten Teil anders ausfällt, ist natürlich, dass man 2004 in ein Produkt aus sechs verschiedenen ganzzahligen Faktoren zerlegen kann, nämlich 2004 = 1 . (- 1) . 2 . (- 2) . 3 . 167.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File

![\includegraphics[width=6cm]{fahrrad.eps}](img4.png)