Beispiellösungen zu Aufgabenblatt 46

aktualisiert: 12. Oktober 2005

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Aufgabe 1

Es ist Wahlzeit, und da wird ja immer fleißig gerechnet ... Svenja zum Beispiel überlegt sich am Wahltag, ob sie noch wählen gehen will. Sie spekuliert: ,,Wenn ich nicht wähle, fällt meine Partei in meinem Wahlbezirk (Wahllokal) bestimmt unter die 5-Prozent-Hürde. Wenn ich aber wählen gehe, könnte es sogar sein, dass sie auf einen zweistelligen Wert kommt.``

Welche Annahmen hat Svenja über die Wählerschaft ihrer Partei und die Wahlbeteiligung insgesamt in ihrem Wahlbezirk gemacht? (Kannst du dir vorstellen, wo Svenja wohnt?)

Lösung:

Zunächst ,,grob gesagt``: Das sieht alles sehr merkwürdig aus! Denn eine einzige Stimme macht mehr als 5 Prozentpunkte aus, während alle anderen Stimmen für Svenjas Partei weniger als 5 Prozent wert sind? Das geht nur, wenn es gar keine anderen Stimmen gibt; und dann darf es inklusive Svenja nicht mehr als 10 Wähler geben, damit ihre Partei mit ihrer einen Stimme auf ein zweistelliges Ergebnis kommt.

Diese Argumentation ist zwar an sich richtig, aber doch recht schwammig formuliert; wir wollen es auch noch ganz korrekt mit (einfachen) Formeln probieren (wobei sich übrigens genau die Überlegungen vom Anfang darin verstecken!):

Sei n die Gesamtzahl der Wähler ohne Svenja, und p sei die Anzahl derjenigen Wähler ohne Svenja, die Svenjas Wunschpartei wählen. Sollte n = 0 sein, stimmt schon einmal offensichtlich Svenjas Überlegung; im Folgenden sei n $\neq$ 0. Nach Voraussetzung gilt dann:

$\displaystyle {\frac{{p}}{{n}}}$ < 0, 05, $\displaystyle {\frac{{p+1}}{{n+1}}}$ $\displaystyle \geq$ 0, 10.

Differenzbildung führt zu

0, 05 < $\displaystyle {\frac{{p+1}}{{n+1}}}$ - $\displaystyle {\frac{{p}}{{n}}}$ $\displaystyle \leq$ $\displaystyle {\frac{{p+1}}{{n}}}$ - $\displaystyle {\frac{{p}}{{n}}}$ = $\displaystyle {\frac{{1}}{{n}}}$ ,

außerdem gilt ja ${\frac{{p}}{{n}}}$ < 0, 05 , insgesamt also

p^.0, 05 $\displaystyle \leq$ $\displaystyle {\frac{{p}}{{n}}}$ < 0, 05.

Daraus folgt unmittelbar p = 0. Und dann folgt aus der zweiten gegebenen Ungleichung ${\frac{{1}}{{n+1}}}$ $\geq$ 0, 10 , also n $\leq$ 9. Damit nimmt Svenja an, dass sie die einzige Anhängerin ihrer Partei ist und dass außer ihr in ihrem Wahlbüro höchstens neun weitere Leute wählen. Es ist also die Wahlbeteiligung sehr niedrig - oder der Wahlbezirk sehr klein. Und solch einen kleinen Wahlbezirk gibt es tatsächlich: Die Gemeinde Hallig Gröde in Schleswig-Holstein! Vermutlich wohnt Svenja somit dort.

Denn vor 7 Jahren kann unser konstruierter Fall sogar Realität gewesen sein: Damals gab es auf Hallig Gröde (bei Husum im Wattenmeer gelegen) elf Wahlberechtigte, von denen zwei nicht zur Wahl gingen, und es entfiel auf eine der Parteien (die Grünen) genau eine Stimme. (Quelle dazu: http://www.rz-online.com/on/02/09/10/topnews/wahl-klein.htm)

In diesem Jahr, 2005, gab es auf Hallig Gröde 12 Wahlberechtigte, von denen 11 wählten, also zu viele für unsere Aufgabe: Die beiden Parteien mit genau einer Stimme (Grüne und Linke) kamen auf je ,,nur`` 9,1 Prozent (Quelle: http://www.statistik-sh.de/BW05/Aktuell/BW54039.htm).

Aufgabe 2

Zu Ehren des 46. Aufgabenblattes: Finde alle Paare (a, b) positiver ganzer Zahlen, für die

$\displaystyle {\frac{{1}}{{a}}}$ + $\displaystyle {\frac{{2}}{{b}}}$ = $\displaystyle {\frac{{3}}{{46}}}$

gilt.

Lösung:

Äquivalente Umformungen der Gleichung führen der Reihe nach zu den Gleichungen:

b + 2a	=	$\displaystyle {\frac{{3}}{{46}}}$ ab
46^.3b + 92^.3a	=	9ab
46^.92	=	9ab - 46^.3b - 92^.3a + 46^.92 = (3a - 46)(3b - 92).

Die beiden Faktoren (3a - 46) und (3b - 92) müssen also zueinander komplementäre Teiler von 46^.92 = 4232 = 2^{3 .}23² sein. Diese listen wir in folgender Tabelle auf; dabei ist die Zuordnung zu den beiden Faktoren deswegen eindeutig, weil 46 und 92 (und damit auch 3a - 46 und 3b - 92) verschiedene Reste beim Teilen durch 3 lassen.

Teiler1 = 3a - 46		Teiler2 = 3b - 92		a	b	Probe: $\displaystyle {\frac{{1}}{{a}}}$ + $\displaystyle {\frac{{2}}{{b}}}$
	4232		1	1426	31	$\displaystyle {\frac{{3}}{{46}}}$
	2		2116	16	736	$\displaystyle {\frac{{3}}{{46}}}$
	1058		4	368	32	$\displaystyle {\frac{{3}}{{46}}}$
	8		529	18	207	$\displaystyle {\frac{{3}}{{46}}}$
	23		184	23	92	$\displaystyle {\frac{{3}}{{46}}}$
	92		46	46	46	$\displaystyle {\frac{{3}}{{46}}}$

Ganz fertig sind wir noch nicht, zumindest formell: Wir müssen uns auch über die negativen Teiler Gedanken machen! Damit aber a und b positiv ganzzahlig werden (wie verlangt), darf der eine Teiler nicht kleiner als -43, der andere nicht kleiner als -89 sein. Damit wäre bei negativen Faktoren ihr Produkt jedoch kleiner gleich (- 43)^.(- 89) = 3827 < 4232, was ein Widerspruch ist.

Somit sind die Lösungspaare (a, b) genau die sechs Paare (16, 736), (18, 207), (23, 92), (46, 46), (368, 32) und (1426, 31).

Aufgabe 3

Christoph hat in seinem Sparschwein Ein- und Zwei-Euro-Münzen (und keine anderen). Wenn er zufällig zwei davon herausnimmt, dann hat er mit genau 50-prozentiger Wahrscheinlichkeit exakt drei Euro herausgenommen. Er weiß auch noch von einer früheren Zählung, dass er mindestens 170 Münzen im Sparschwein hat. Außerdem ist er sich sicher, dass es nicht gleich viele Ein- und Zwei-Euro-Münzen sind. Kann er sich mit dem Geld im Sparschwein seinen großen Wunsch, einen Computer für 289 Euro, kaufen?

Lösung:

Angenommen, in Christophs Sparschwein befinden sich e Ein-Euro- und z Zwei-Euro-Münzen. Die Wahrscheinlichkeit, aus dem Sparschwein genau drei Euro mit zwei Münzen herauszunehmen, ist gleich der Wahrscheinlichkeit, eine Ein- und eine Zwei-Euro-Münze zu ziehen. Wenn man sich die Münzen als nacheinander gezogen denkt, gibt es dafür zwei Möglichkeiten: Erst die Ein-Euro-Münze (Wahrscheinlichkeit: ${\frac{{e}}{{e+z}}}$ ), dann die Zwei-Euro-Münze (Wahrscheinlichkeit: ${\frac{{z}}{{e+z-1}}}$ , insgesamt also ${\frac{{e}}{{e+z}}}$ ^. ${\frac{{z}}{{e+z-1}}}$ ) oder umgekehrt (Wahrscheinlichkeit dafür: ${\frac{{z}}{{e+z}}}$ ^. ${\frac{{e}}{{e+z-1}}}$ ).

Die Wahrscheinlichkeit dafür, genau drei Euro zu ziehen, ist daher genau

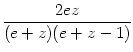$\displaystyle {\frac{{2ez}}{{(e+z)(e+z-1)}}}$ .

(Für diejenigen, die bereits Binomialkoeffizienten kennen: Auch damit kommt man - natürlich - auf dasselbe Ergebnis: Man hat offenbar genau $\binom{e+z}{2}$ = ${\frac{{(e+z)(e+z-1)}}{{2}}}$ Möglichkeiten, zwei Münzen herauszunehmen, und es gibt e^.z Möglichkeiten darunter, bei denen die beiden gezogenen Münzen verschiedene Werte anzeigen. Die Wahrscheinlichkeit beträgt folglich ${\frac{{e\cdot z}}{{\ \frac{(e+z)(e+z-1)}{2}\ }}}$ = ${\frac{{2ez}}{{(e+z)(e+z-1)}}}$ .)

Diese Wahrscheinlichkeit soll nun genau 0, 5 sein. Man erhält die Beziehung

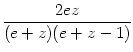	$\displaystyle {\frac{{2ez}}{{(e+z)(e+z-1)}}}$	=	$\displaystyle {\frac{{1}}{{2}}}$
$\displaystyle \iff$	4ez	=	(e + z)² - (e + z)
$\displaystyle \iff$	(e + z)	=	(e + z)² - 4ez = (e - z)².

Die Anzahl der Münzen e + z im Sparschwein muss somit eine Quadratzahl sein! Setzt man e - z = n, so folgt e + z = n² und damit

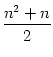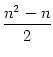e = $\displaystyle {\frac{{n^2+n}}{{2}}}$ und z = $\displaystyle {\frac{{n^2-n}}{{2}}}$ .

In Abhängigkeit von n hat Christoph also genau n² $\geq$ 170 Münzen im Sparschwein, die einen Gesamtwert von

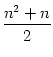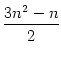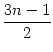
e + 2z = $\displaystyle {\frac{{n^2+n}}{{2}}}$ + n² - n = $\displaystyle {\frac{{3n^2-n}}{{2}}}$ = n^. $\displaystyle {\frac{{3n-1}}{{2}}}$

Euro haben. Die Beziehung n² $\geq$ 170 ergibt | n| $\geq$ 14. Jedes hiermit geeignete n liefert auch in der Tat ein Paar (e, z), für das die angegebene Wahrscheinlichkeit 0, 5 ist, denn wir haben nur Äquivalenzumformungen verwendet.

Da mit | n| für festes Vorzeichen von n auch e + 2z wächst, wäre der für Christoph schlimmste Fall einer der Fälle n = ±14, und von diesen beiden Möglichkeiten wäre die schlimmere n = + 14, weil er dann mehr Ein- als Zwei-Euro-Münzen hat: Er hätte genau 105 Ein-Euro- und 91 Zwei-Euro-Münzen im Sparschwein, die einen Gesamtwert von nur 287 Euro haben.

Christoph kann sich daher leider nicht sicher sein, sich seinen Wunsch erfüllen zu können.

PS: In der Tat ist dies aber der einzige Fall, in dem sein Geld nicht reichen würde; für alle anderen erlaubten n ergibt sich ein ausreichender Geldbetrag.

Aufgabe 4

Um seiner Tochter Rapanuia eine Freude zu machen, verwandelt Lord Stevenson die Osterinsel, auf der sie gerade im Urlaub weilen, in eine Schatzinsel. Bekanntermaßen stehen auf der Osterinsel 638 Moais, kolossale Steinstatuen unbekannten Zweckes. Jeweils in der Mitte zwischen zwei Moais versteckt der Lord einen Goldtaler. Allerdings versteckt er an keinem Ort mehr als einen Taler. Zeige, dass Rapanuia mindestens 1273 Goldtaler finden kann.

Könnte der Lord - wäre er nur stark genug - die Steinfiguren so umstellen, dass er nicht mehr als 1273 Goldtaler verstecken muss?

Lösung:

Zuerst zeichnen wir auf der Insel (in Gedanken) alle Geraden durch je zwei Steinstatuen ein und wählen dann eine Gerade g, die keine dieser endlich vielen (!) Geraden senkrecht schneidet. Dann fällen wir von jeder Statue A senkrecht das Lot auf die Gerade g und kennzeichnen den Lotfußpunkt A'.

$\includegraphics[]{loes46_4_a}$

Auf diese Art erhalten wir 638 Punkte auf der Geraden g. Diese Punkte sind alle (paarweise - wie der Mathematiker sagt) verschieden, denn hätten zwei Steinstatuen A und B denselben Lotfußpunkt auf g, so läge dieser auf der Geraden durch A und B, insbesondere wäre diese Gerade senkrecht zu g, im Widerspruch zur Wahl von g.

Auch von der Mitte M zwischen zwei Statuen A und B fällen wir jeweils das Lot auf g und markieren den Lotfußpunkt M'. Nach dem Strahlensatz ist M' der Mittelpunkt der Strecke A'B'.

Nun haben wir auf der Geraden g eine ähnliche Situation wie am Anfang auf der Insel. Auf der Geraden g liegen 638 Lotfußpunkte der Statuen und wir wollen zählen, wie viele verschiedene Mittelpunkte es zwischen ihnen mindestens geben muss. Dabei sei noch kurz erwähnt, dass die Lotfußpunkte der Statuen alle verschieden sind, die Lotfußpunkte verschiedener Mittelpunkte aber gleich sein können. Aber wichtig für uns ist nur, dass es nicht mehr Mittelpunkte geworden sein können.

Betrachten wir einen Ausschnitt von drei benachbarten ,,Statuen`` A, B, C auf g, so liegt der Mittelpunkt M(A, B) der Nachbarn A und B zwischen A und B, und der Mittelpunkt M(B, C) liegt zwischen B und C, die beiden Mittelpunkte sind also verschieden. Folglich sind auch alle 638 - 1 Mittelpunkte zwischen je zwei benachbarten Statuen auf g verschieden.

$\includegraphics[]{loes46_4_b}$

Außerdem liegt der Mittelpunkt M(A, C) von A und C zwischen den beiden ,,Nachbarmittelpunkten`` M(A, B) und M(B, C), ist also von diesen beiden und auch allen anderen Nachbarmittelpunkten verschieden.

Zählen wir nun also alle solchen Mittelpunkte zwischen einer Statue und ihrem übernächsten Nachbarn, so erhalten wir noch 638 - 2 weitere verschiedene Mittelpunkte.

Insgesamt gibt es auf der Geraden g und damit auch auf der Insel mindestens 637 + 636 = 1273 verschiedene Mittelpunkte.

Der Lord wird zwar kaum Chancen haben, die riesigen Statuen auf der Insel umzustellen - die Wissenschaftler rätseln noch heute, wie die Kolosse ohne moderne Kräne errichtet werden konnten - aber stünden sie alle in gleichem Abstand in einer Reihe, so müsste er tatsächlich nur 1273 Goldtaler verstecken, nämlich 637 jeweils in der Mitte zwischen zwei benachbarten Statuen und 636 unter den Statuen selbst, außer unter den beiden äußeren. Denn wenn wir die Statuen der Reihe nach von 1 bis 638 durchnummerieren, so ist wegen des gleichen Abstands der Statuen die Mitte zwischen den Statuen i und j entweder - wenn i + j gerade ist - genau bei der Statue ${\frac{{i+j}}{{2}}}$ oder - wenn i + j ungerade ist - genau in der Mitte zwischen den Statuen ${\frac{{i+j-1}}{{2}}}$ und ${\frac{{i+j+1}}{{2}}}$ .

http://www.lib.utexas.edu/maps/islands_oceans_poles/easter_island.jpg – Karte der Osterinsel und der Statuen aus der Kartensammlung der Perry-Castañeda Bibliothek.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File