Beispiellösungen zu Aufgabenblatt 49

aktualisiert: 7. Februar 2006

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1


Bei Familie Lösche wird Ästhetik groß geschrieben: Man versucht, die vier Kerzen am Adventskranz möglichst gleichmäßig niederzubrennen; am schönsten ist es, wenn sie am Heiligen Abend alle gleich weit heruntergebrannt sind. Wie üblich wird am ersten Advent genau eine Kerze angezündet, am zweiten Advent werden genau zwei, am dritten Advent genau drei und am vierten Advent werden alle vier Kerzen angezündet und jede angezündete Kerze brennt für genau eine Stunde, bevor der Sohn der Familie sie auspusten darf. Können die Lösches es schaffen, dass die Kerzen zu Weihnachten alle gleich weit abgebrannt sind?

Wie sähe es aus, wenn es n Adventssonntage und dementsprechend n Kerzen gäbe?


Lösung:


Nein, Familie Lösche kann es nicht schaffen, dass die Kerzen zu Weihnachten alle gleich weit abgebrannt sind: Sei x die Länge, um die eine Kerze in einer Stunde herunterbrennt. Dann sind bis Weihnachten alle Kerzen zusammen um (1 + 2 + 3 + 4) . x = 10x heruntergebrannt. Da 10 nicht durch 4 teilbar ist, ist es nicht möglich, bis Weihnachten alle Kerzen gleichmäßig herunterzubrennen.

Bei n Adventssonntagen würden die Kerzen bis Weihnachten gemeinsam um (1 + 2 +...+ n) . x = $ {\frac{{n\cdot (n+1)}}{{2}}}$x herunterbrennen. Damit überhaupt ein gleichmäßiges Herunterbrennen möglich ist, muss folglich $ {\frac{{n\cdot (n+1)}}{{2}}}$ durch n, die Anzahl der Kerzen, teilbar sein. Dies ist genau dann der Fall, wenn n + 1 gerade, also n ungerade ist. Und in der Tat reicht das schon für die Existenz einer solchen Möglichkeit aus: Zum Beispiel kann man sich für 1 $ \leq$ k $ \leq$ $ {\frac{{n-1}}{{2}}}$ am k-ten Advent beliebige k Kerzen aussuchen; wenn man dann am (n - k)-ten Advent (also vom $ {\frac{{n+1}}{{2}}}$-ten bis zum (n - 1)-ten Advent) genau diejenigen Kerzen anzündet, die am k-ten Advent nicht leuchteten, sind am vorletzten und damit auch am letzten Advent alle Kerzen gleich weit heruntergebrannt.


Aufgabe 2


Die Firma ,,Niko & Laus`` GmbH hat eine tolle Geschäftsidee: Sie will rechteckige Adventskalender mit ganzzahligen Seitenlängen (in Zentimetern) herstellen, bei denen das n-te Türchen ebenfalls rechteckig mit ganzzahligen Seitenlängen ist und genau den Flächeninhalt n cm2 hat. Dabei sollen die Türchenseiten parallel zu den Seiten des Kalenders liegen.

Passt ein solcher Kalender auf ein Rechteck, dessen Seiten beide kürzer als 24 cm sind? Wenn ja, was ist die kleinstmögliche Fläche eines solchen Kalenders?

Hinweis: Die Türchen des Kalenders dürfen auch direkt aneinander oder auch direkt an den Rand des Kalenders stoßen.


Lösung:


Ein Beispiel für einen Kalender, dessen Seiten beide kürzer als 24 cm sind, ist der folgende:

\includegraphics[]{loes49_2}

Dieser hat die Abmessungen 14 cm . 23 cm = 322 cm2. Dies ist auch die kleinstmögliche Fläche für einen solchen Kalender. Denn um alle Türchen unterzubringen, muss das Rechteck mindestens 1 + 2 + 3 + ... + 24 = $ {\frac{{24 \cdot 25}}{{2}}}$ = 300 cm2 groß sein. Da 23 eine Primzahl ist, hat dieses Türchen die Abmessungen 1 . 23. Somit ist eine Seite des Kalenders mindestens 23 cm lang. Da 23 . 13 < 300 ist, muss die andere Seite entsprechend mindestens 14 cm lang sein. Der obige Kalender besitzt also minimale Abmessungen.


Aufgabe 3


Auch der Weihnachtsmann denkt (öko-)logisch! Er will für Peter einen Fußball mit Durchmesser 30 cm und sechs Tennisbälle mit Durchmesser von je 8 cm in einer quaderförmigen Schachtel verpacken. Welches ist die Schachtel mit der kleinsten Oberfläche, für die dies möglich ist?


Lösung:


Eine quaderförmige Schachtel, in die (zunächst nur) der Fußball hineinpassen soll, muss offenbar mindestens 30 cm hoch, breit und tief sein. Unter allen Schachteln, die diese Eigenschaft haben, ist die würfelförmige Schachtel mit Seitenlänge 30 cm diejenige mit der kleinsten Oberfläche.

Wir zeigen nun, dass in diese Schachtel zusätzlich zum Fußball auch noch bis zu acht der gegebenen Tennisbälle passen. Hierzu berechnen wir den Radius des größten Tennisballs, den man zusätzlich zum Fußball noch in eine Ecke des Würfels packen kann.

Wir berechnen also den Radius r einer Kugel, die drei an einer Ecke anstoßende Seitenflächen eines Würfels mit Seitenlänge a von innen und eine dem Würfel einbeschriebene Kugel von außen berührt.

\includegraphics[width=5.5cm]{fussball3.eps}        \includegraphics[width=7cm]{loes49_3}

Wie in der Abbildung angedeutet, gilt hierbei:

$\displaystyle \sqrt{{3}}$ . r + r + $\displaystyle {\frac{{a}}{{2}}}$ = $\displaystyle \sqrt{{3}}$ . $\displaystyle {\frac{{a}}{{2}}}$.

Nach r umgeformt ergibt dies

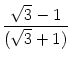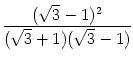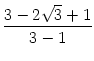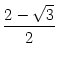r = $\displaystyle {\frac{{\sqrt{3}-1}}{{(\sqrt{3}+1)}}}$ . $\displaystyle {\frac{{a}}{{2}}}$ = $\displaystyle {\frac{{(\sqrt{3}-1)^2}}{{(\sqrt{3}+1)(\sqrt{3}-1)}}}$ . $\displaystyle {\frac{{a}}{{2}}}$ = $\displaystyle {\frac{{3 - 2 \sqrt{3} + 1}}{{3-1}}}$ . $\displaystyle {\frac{{a}}{{2}}}$ = $\displaystyle {\frac{{2-\sqrt{3}}}{{2}}}$ . a.

Setzt man hier nun a = 30 cm ein, so liefert der Taschenrechner r $ \approx$ 4, 019 cm > 4 cm. Für eine genaue Abschätzung, die hierzu nötig ist, muss man (2 - $ \sqrt{{3}}$) . 15 > 4 zeigen. Dies ist aber äquivalent zu 26 > 15$ \sqrt{{3}}$, und die Gültigkeit dieser Ungleichung folgt durch Wurzelziehen aus 262 = 676 > 675 = 152 . 3.

Also passt in der Tat in jede der acht Ecken des Würfels noch ein Tennisball mit Durchmesser 8 cm. Die gesuchte Schachtel ist daher die beschriebene würfelförmige und sie hat eine Oberfläche von 6 . (30 cm)2 = 5400 cm2.


Aufgabe 4


Denke dir eine natürliche Zahl n, wie zum Beispiel n = 12. Nun mache eine Liste der Teiler von n, in unserem Fall also 1, 2, 3, 4, 6, 12. Anschließend bestimme für jeden dieser Teiler die Anzahl seiner Teiler und schreibe diese Anzahlen in eine zweite Liste. In unserem Beispiel hat 1 genau einen Teiler, 2 hat zwei Teiler, ebenso 3; 4 hat drei Teiler, 6 hat vier Teiler und 12 hat sechs Teiler. Unsere zweite Liste ist daher 1, 2, 2, 3, 4, 6. Zu guter Letzt addiere die Kuben dieser Zahlen, im Beispiel ergibt das 13 + 23 + 23 + 33 + 43 + 63 = 324.

Zeige, dass das Ergebnis stets eine Quadratzahl ist!


Lösung:


Wir schreiben zunächst kurz $ \mbox{$\tau(n)$}$ für die Anzahl der Teiler der natürlichen Zahl n. Dann ist also zu zeigen, dass für alle natürlichen Zahlen n die Zahl

F(n) : = $\displaystyle \sum_{{d\vert n}}^{}$$\displaystyle \tau$(d )3

eine Quadratzahl ist. Die hier verwendete Schreibweise $ \sum\limits_{{d\vert n}}^{}$ bedeutet, dass man den Wert von $ \mbox{$\tau(d)$}$3 für alle Teiler d von n summiert: ,,$ \Sigma$`` (das griechische große Sigma) ist das Summenzeichen, und unter ihm steht (hier in Kurzform), für welche Werte welches Parameters man aufsummiert: ,,d | n`` liest man als ,,d teilt n``, im Ausdruck rechts vom Summenzeichen soll also d als Wert jeden Teiler von n annehmen, und diese Ausdrücke werden dann addiert.

Betrachten wir dazu zunächt einmal einen Spezialfall: Sei n = pk, k $ \geq$ 0, eine Primzahlpotenz. Dann können wir zunächst recht einfach eine Liste aller Teiler von n angeben, nämlich 1, p, p2,..., pk. Also ist

F(pk) = $\displaystyle \sum_{{d\vert p^k}}^{}$$\displaystyle \mbox{$\tau(d)$}$3 = $\displaystyle \mbox{$\tau(1)^3+\tau(p)^3+\tau(p^2)^3+\ldots+\tau(p^k)^3$}$  
  = 13 + 23 + 33 +...+ (k + 1)3.  

Hier haben wir benutzt, dass ein Teiler der Form pt ganz entsprechend genau die t + 1 Teiler 1, p, p2,..., pt hat.

Letzteres ist nun eine bekannte Summe, die man aus dem Schulunterricht kennt oder in (den meisten) Formelsammlungen findet:

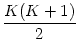
13 + 23 + 33 +...+ K3 = $\displaystyle \left(\vphantom{\frac{K(K+1)}{2}}\right.$$\displaystyle {\frac{{K(K+1)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{K(K+1)}{2}}\right)^{2}_{}$.

Ein Beweis dieser Formel gelingt zum Beispiel mittels Induktion nach K. Für K = 1 gilt sie offenbar und im Induktionsschritt zeigt man:

13 + 23 +...+ K3 + (K + 1)3 = 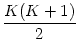$\displaystyle \left(\vphantom{\frac{K(K+1)}{2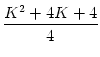}}\right.$$\displaystyle {\frac{{K(K+1)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{K(K+1)}{2}}\right)^{2}_{}$ + (K + 1)3    
  = (K + 1)2 . $\displaystyle \left(\vphantom{\frac{K^2 + 4K + 4}{4}}\right.$$\displaystyle {\frac{{K^2 + 4K + 4}}{{4}}}$$\displaystyle \left.\vphantom{\frac{K^2 + 4K + 4}{4}}\right)$    
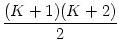  = $\displaystyle \left(\vphantom{\frac{(K+1)(K+2)}{2}}\right.$$\displaystyle {\frac{{(K+1)(K+2)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{(K+1)(K+2)}{2}}\right)^{2}_{}$.    

Da der Term $ {\frac{{K(K+1)}}{{2}}}$ in jedem Fall eine ganze Zahl ist, weil entweder K oder K + 1 gerade ist, ist die gesuchte Summe also in diesem Spezialfall stets eine Quadratzahl.

Um nun die Aussage auch für allgemeine n zu beweisen, benutzen wir folgenden Begriff aus der Zahlentheorie: Eine Abbildung (Funktion) f, die jeder natürlichen Zahl eine andere natürliche Zahl zuordnet, heißt multiplikativ, wenn für jedes Paar teilerfremder Zahlen m, n gilt: f (m . n) = f (m) . f (n).

Wir wollen zeigen, dass unsere gesuchte Funktion F multiplikativ ist. Wenn uns dies gelingt, dann sind wir fertig, denn jede natürliche Zahl n hat eine eindeutige Primfaktorzerlegung der Form n = p1k1 . p2k2 . ... . p$\scriptstyle \ell$k$\scriptscriptstyle \ell$ mit verschiedenen Primzahlen p1 bis p$\scriptstyle \ell$ und es gilt dann

F(n) = F(p1k1 . p2k2 . ... . p$\scriptstyle \ell$k$\scriptscriptstyle \ell$)    
  = F(p1k1) . F(p2k2 . ... . p$\scriptstyle \ell$k$\scriptscriptstyle \ell$)    
  = F(p1k1) . F(p2k2) . ... . F(p$\scriptstyle \ell$k$\scriptscriptstyle \ell$)    
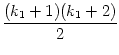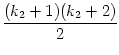  = $\displaystyle \left(\vphantom{\frac{(k_1+1)(k_1+2)}{2}}\right.$$\displaystyle {\frac{{(k_1+1)(k_1+2)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{(k_1+1)(k_1+2)}{2}}\right)^{2}_{}$ . $\displaystyle \left(\vphantom{\frac{(k_2+1)(k_2+2)}{2}}\right.$$\displaystyle {\frac{{(k_2+1)(k_2+2)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{(k_2+1)(k_2+2)}{2}}\right)^{2}_{}$ . ... . 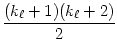$\displaystyle \left(\vphantom{\frac{(k_\ell+1)(k_\ell+2)}{2}}\right.$$\displaystyle {\frac{{(k_\ell+1)(k_\ell+2)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{(k_\ell+1)(k_\ell+2)}{2}}\right)^{2}_{}$    
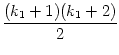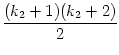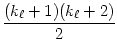  = $\displaystyle \left(\vphantom{\frac{(k_1+1)(k_1+2)}{2}\cdot\frac{(k_2+1)(k_2+2)}{2} \cdot\ldots\cdot\frac{(k_\ell+1)(k_\ell+2)}{2}}\right.$$\displaystyle {\frac{{(k_1+1)(k_1+2)}}{{2}}}$ . $\displaystyle {\frac{{(k_2+1)(k_2+2)}}{{2}}}$ . ... . $\displaystyle {\frac{{(k_\ell+1)(k_\ell+2)}}{{2}}}$$\displaystyle \left.\vphantom{\frac{(k_1+1)(k_1+2)}{2}\cdot\frac{(k_2+1)(k_2+2)}{2} \cdot\ldots\cdot\frac{(k_\ell+1)(k_\ell+2)}{2}}\right)^{2}_{}$.    

Das ist in jedem Fall eine Quadratzahl.

Es bleibt also die Multiplikativität von F zu zeigen.

Hierzu zeigen wir zwei kleine Hilfsaussagen über multiplikative Funktionen.

Hilfsaussage 1: Ist f multiplikativ, so ist auch f 3 multiplikativ, wobei f 3(n) = f (n)3 ist.

Beweis der Hilfsaussage 1: Dies ist nicht schwer: Es gilt für teilerfremde m und n nämlich f 3(m . n) = $ \left(\vphantom{f(m\cdot n)}\right.$f (m . n)$ \left.\vphantom{f(m\cdot n)}\right)^{3}_{}$ = f (m)3 . f (n)3 = f 3(m) . f 3(n).



Hilfsaussage 2: Ist f multiplikativ, so ist auch g(n) : = $ \sum\limits_{{d\vert n}}^{}$f (d ) multiplikativ.

Beweis der Hilfsaussage 2: Das ist schon etwas schwieriger. Es gilt aber wieder für teilerfremde Zahlen m und n:

g(m) . g(n) = $\displaystyle \sum_{{r\vert m}}^{}$f (r) . $\displaystyle \sum_{{s\vert n}}^{}$f (s)    
  = $\displaystyle \sum_{{r\vert m; s\vert n}}^{}$f (r)f (s)    
  = $\displaystyle \sum_{{r\vert m; s\vert n}}^{}$f (rs).    

Letzteres folgt aus der Tatsache, dass f multiplikativ ist und für teilerfremde m und n auch jeder Teiler r von m und jeder Teiler s von n zueinander teilerfremd sind.

Ausserdem folgt aus der Teilerfremdheit von m und n, dass tatsächlich jeder Teiler von m . n eindeutig als Produkt eines Teilers r von m und eines Teilers s von n geschrieben werden kann1.

Deswegen tritt in der letzten Summe jeder Teiler t = rs von m . n genau einmal auf. Es ist also tatsächlich

g(m) . g(n) = $\displaystyle \sum_{{t\vert m\cdot n}}^{}$f (t) = g(m . n).

Mit Hilfe dieser beiden Aussagen können wir nun die Multiplikativität von F leicht zeigen. Zunächst ist die Funktion f (n) = 1, die allen n die Zahl 1 zuordnet, sicher multiplikativ. Also ist, nach Hilfsaussage 2, auch $ \mbox{$\tau(n)$}$ = $ \sum\limits_{{d\vert n}}^{}$1 multiplikativ, wegen Hilfsaussage 1 folgt dann die Multiplikativität von $ \tau^{3}_{}$ und erneut mit Hilfsaussage 2 kann man dann auf die Multiplikativität von F(n) = $ \sum\limits_{{d\vert n}}^{}$$ \mbox{$\tau(n)$}$3 schließen.

Damit ist der Beweis vollständig erbracht.


Fußnoten

... kann1
Beachte, dass dies für nicht teilerfremde m, n im Allgemeinen nicht gilt!
drucken Zum Ausdrucken als pdf-File oder als ps-File