 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Aufgabe 1
Kristin soll einen Bruch finden, der zwischen den beiden Brüchen
![]() und
und
![]() liegt. Ratlos versucht sie
liegt. Ratlos versucht sie
![]() . Ist dies eine Lösung ihres Problems?
. Ist dies eine Lösung ihres Problems?
Liegt der Bruch
![]() immer zwischen den beiden Brüchen
immer zwischen den beiden Brüchen
![]() und
und
![]() (mit positiven ganzen Zahlen
a, b, c, d)?
Wie kann man, ohne zu rechnen, sofort entscheiden, ob
(mit positiven ganzen Zahlen
a, b, c, d)?
Wie kann man, ohne zu rechnen, sofort entscheiden, ob
![]() näher
an
näher
an
![]() oder an
oder an
![]() liegt?
liegt?
Lösung:
Es ist
= 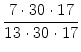 = = |
||
= 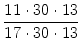 = = |
||
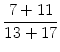 |
= 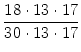 = = |
Nun sieht man:
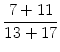 =
=
Gilt für die beiden Brüche
![]() und
und
![]() Gleichheit, so
sind alle drei Brüche gleich, denn aus
Gleichheit, so
sind alle drei Brüche gleich, denn aus
![]() =
= ![]() folgt
c =
folgt
c = ![]() und daher
und daher
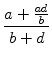 =
= 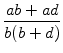 =
=
Im Weiteren sei nun
![]()
![]()
![]() ;
dann kann
o. B. d. A.1angenommen werden, dass
;
dann kann
o. B. d. A.1angenommen werden, dass
![]() <
< ![]() gilt. Dies ist zu
ad < bc äquivalent.
gilt. Dies ist zu
ad < bc äquivalent.
Weiter gilt nun:
| ad | < | bc | |
| ad + ab | < | bc + ab | |
| a(d + b) | < | b(c + a) | |
| < |
und analog gilt:
| ad | < | bc | |
| ad + cd | < | bc + cd | |
| d (a + c) | < | c(b + d ) | |
| < |
Zusammen folgt dann
![]() <
< ![]() <
< ![]() , der neue Bruch
, der neue Bruch
![]() liegt also immer zwischen
liegt also immer zwischen
![]() und
und
![]() .
.
Um eine allgemeine Aussage darüber treffen zu können, wann
![]() näher an
näher an
![]() oder näher an
oder näher an
![]() liegt, betrachten wir den
Abstand d1 von
liegt, betrachten wir den
Abstand d1 von
![]() zu
zu
![]() :
:
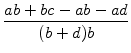
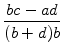
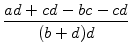
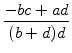
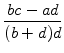
Es folgt also, dass
![]() näher an
näher an
![]() liegt,
wenn b > d ist, und dass
liegt,
wenn b > d ist, und dass
![]() näher an
näher an
![]() liegt, wenn
d > b ist.
Der neue Bruch liegt also näher an dem Bruch mit dem größeren Nenner.
liegt, wenn
d > b ist.
Der neue Bruch liegt also näher an dem Bruch mit dem größeren Nenner.
Gilt b = d, so sind d1 und d2 gleich groß und
![]() liegt genau in der Mitte der Brüche
liegt genau in der Mitte der Brüche
![]() und
und
![]() .
.
Aufgabe 2
Auf wie viele Arten kann man 2006 als Summe aufeinander folgender positiver
ganzer Zahlen darstellen?
Welches ist das nächste Jahr, dessen Jahreszahl nur eine derartige
Darstellung erlaubt?
Hinweis: Zum Beispiel hat 10 genau die zwei Darstellungen 10 und 1 + 2 + 3 + 4.
Lösung:
Sei a, a + 1, ..., a + k eine solche Zahlenfolge mit Summe n, dann
gilt:
| 2n | = ![$\displaystyle \begin{array}[t]{*{8}{c}} & a &+& (a+1) &+ \ldots +& (a+k-1) &+& (a+k)\\ + & (a+k) &+& (a+k-1)&+ \ldots +& (a+1) &+& a \end{array}$](img44.png) |
|
| = (k + 1) . (2a + k). |
Offenbar ist k + 1 < 2a + k, d. h. k + 1 ist stets der kleinere Teiler.
Wir zeigen nun, dass für jeden ungeraden Teiler von n genau eine Folge mit
den geforderten Eigenschaften existiert. Dazu müssen wir zwei Richtungen
zeigen:
(1) Sei t ein ungerader Teiler von n, dann gibt es eine dazugehörende
Folge, die die Voraussetzungen erfüllt.
Beweis zu (1): Zunächst haben wir
2n = t . r mit einer ganzen Zahl
r. Da 2n gerade ist, muss auch r gerade sein. Ist nun t < r, so setzen
wir t = k + 1 und r = 2a + k. Wir finden somit eine Lösung des Problems durch die
Wahlen k = t - 1 und
a = ![]() . Eine Probe ergibt, dass diese
Folge wirklich die geforderten Eigenschaften hat, insbesondere ist a eine
positive ganze Zahl. Ist andersherum t > r, so setzen wir t = 2a + k und
r = k + 1 und erhalten analog zu den obigen Überlegungen mit k = r - 1 und
a =
. Eine Probe ergibt, dass diese
Folge wirklich die geforderten Eigenschaften hat, insbesondere ist a eine
positive ganze Zahl. Ist andersherum t > r, so setzen wir t = 2a + k und
r = k + 1 und erhalten analog zu den obigen Überlegungen mit k = r - 1 und
a = ![]() eine Lösung.
eine Lösung.
(2) Es gibt keine weiteren solche Folgen.
Beweis zu (2): Zu jeder Folge gehört eine Zerlegung 2n = (k + 1)(2a + k). Dabei ist k + 1 genau dann gerade, wenn k ungerade ist, also genau dann, wenn 2a + k ungerade ist. Somit gehört zu jeder Folge ein ungerader Teiler von 2n und damit auch von n. Es muss nur noch gezeigt werden, dass dieser Teiler in Teil (1) zu derselben Folge führt. Das jedoch ist der Fall, weil k + 1 stets der kleinere Teiler ist; die Zuordnung in Teil (1) berücksichtigt dies.
Für n = 2006 gibt es also vier solcher Summendarstellungen, da 2006 gerade
die vier ungeraden Teiler 1, 17, 59 und 1003 hat. Diese vier
Darstellungen sind:
| 2006 | |
| 110 + 111 +...+ 126 | |
| 5 + 6 +...+ 63 | |
| 500 + 501 + 502 + 503 |
Eine Zahl besitzt genau dann nur eine solche Darstellung, wenn sie genau einen
ungeraden Teiler hat. Dies ist genau dann der Fall, wenn die Zahl eine reine
Zweierpotenz ist.
Die nächste Jahreszahl mit nur einer Darstellung ist folglich
2048(= 211).
Aufgabe 3
Der Neubau des Theaters der Stadt Göttingen hat einen Zuschauerraum mit dem
Grundriss eines gleichseitigen Dreiecks mit Seitenlänge 50 Meter. Die
Bühne befindet sich in der Mitte einer der Seiten des Dreiecks und ist genau
30 Meter lang. Entlang der anderen beiden Seiten befinden sich die
Sitzplätze. Wo muss man sich hinsetzen, um die beste Sicht auf die Bühne zu
haben, um also die Bühne unter dem größtmöglichen Blickwinkel zu sehen?
Der Oberbürgermeister verlangt, parallel zur Bühne eine zusätzliche Sitzreihe einzubauen, die die beiden anderen Seiten des Dreiecks verbindet.
![\includegraphics[width=4.5cm]{buehne5}](img47.png)
In der Mitte dieser Reihe soll die Bürgermeisterloge von allen vorhandenen Sitzen die beste Sicht auf die Bühne garantieren. Wie lang ist diese Sitzreihe dann mindestens?
Lösung:
Zu dieser Aufgabe gibt es einige verschiedene Lösungswege. Wir wollen hier einen Weg angeben, der möglichst ,,elementar`` ist - also mit Elementargeometrie arbeitet.
Nach dem Umfangswinkel- oder Peripheriewinkelsatz liegen bekanntlich alle diejenigen Punkte, von denen aus man die Bühne unter einem bestimmten Winkel sieht, auf einem Kreisbogen, der die beiden Randpunkte A und B der Bühne enthält. Dabei gilt, da ja die Länge der Sehne (das ist hier die Bühnenbreite) fest vorgegeben ist, dass der Blickwinkel um so kleiner wird, je größer der Kreisradius ist. Einen Punkt auf dem Dreiecksrand mit bester Sicht finden wir also, indem wir denjenigen Kreisbogen bestimmen, der zwischen A und B verläuft und eine andere Dreiecksseite (aus Symmetriegründen dann beide) berührt. In der Skizze ist das der durchgezogen gezeichnete Kreisbogen.
![\includegraphics[width=8cm]{buehneloes}](img48.png)
Den Abstand | CT| bestimmen wir über den Tangentensatz: Die Gerade durch C und T ist eine Tangente an diesen Kreis, die Gerade durch C, B und A eine Sekante; nach dem Tangentensatz gilt dann
| | CT|2 = | CA| . | CB| = 40m . 10m = 400m2 | ||
Da eine parallel zur Bühne eingebaute Sitzreihe umso länger wird, je dichter sie an der Bühne ist, ist die kürzeste Sitzreihe, die den Bedingungen an eine Oberbürgermeisterloge genügt, diejenige, die den Kreis der Punkte mit optimaler Sicht gerade tangiert. Um die nötige Länge dieser Sitzreihe zu bestimmen, bestimmen wir zunächst den Radius r des besagten Kreises durch A, B und T. Sein Mittelpunkt sei mit M bezeichnet.
![\includegraphics[width=8cm]{buehneob}](img50.png)
Da der Zuschauerraum ein gleichseitiges Dreieck ist,
ist
![]() TEM = 30o. Außerdem
hat das Dreieck ETM bei T einen rechten Winkel.
Spiegeln wir M an der Geraden ET zu M', so ist ETM eine Hälfte des
gleichseitigen
Dreiecks EM'M, so dass
r = | MT| =
TEM = 30o. Außerdem
hat das Dreieck ETM bei T einen rechten Winkel.
Spiegeln wir M an der Geraden ET zu M', so ist ETM eine Hälfte des
gleichseitigen
Dreiecks EM'M, so dass
r = | MT| = ![]() | ME| =
| ME| = ![]() (r + h)
ist. Daraus
folgt r = h und
mit Pythagoras
(2r)2 = | ME|2 = | MT|2 + | ET|2 = r2 + (| EC| - | CT|)2 = r2 + (30m)2, also
3r2 = 900m2 und
h = r =
(r + h)
ist. Daraus
folgt r = h und
mit Pythagoras
(2r)2 = | ME|2 = | MT|2 + | ET|2 = r2 + (| EC| - | CT|)2 = r2 + (30m)2, also
3r2 = 900m2 und
h = r = ![]() . 10m. h ist die Höhe des gleichseitigen Dreiecks EPQ, das
folglich die Seitenlänge
. 10m. h ist die Höhe des gleichseitigen Dreiecks EPQ, das
folglich die Seitenlänge
![]() h = 20m hat. Die
kürzeste Sitzreihe PQ mit der Möglichkeit für eine Bürgermeisterloge ist
daher 20 m lang.
h = 20m hat. Die
kürzeste Sitzreihe PQ mit der Möglichkeit für eine Bürgermeisterloge ist
daher 20 m lang.
Bemerkungen:
Wegen
| LP| = | BC| = 10m ist PC parallel zu LB, Entsprechendes gilt
für QD und LA. Daher ist auch LBA ein gleichseitiges Dreieck, und
deswegen beträgt der optimale Blickwinkel 60o.
Aus der Umkehrung des Strahlensatzes folgt, dass BT parallel zu ME ist,
also senkrecht auf AB steht. Das ist reiner Zufall; wäre die Bühne breiter,
so würde man vor ihr sitzen, wäre sie schmaler, säße man außerhalb der
Bühnenbreite am besten.
Aufgabe 4
Im Speisesaal des wieder errichteten Klosters Wan-Dan steht ein 250 m langer
und 2 m breiter rechteckiger Tisch, an dem die Mönche jeden Tag ihre
Mahlzeiten einnehmen. Für jeden Mönch muss hierbei der Reinlichkeit halber
ein kreisrundes Platzdeckchen mit Durchmesser 1 m auf den Tisch passen, ohne
über dessen Rand hinauszuragen und ohne mit anderen Platzdeckchen zu
überlappen.
Können an dem Tisch mehr als 500 Mönche gleichzeitig essen?
Lösung:
Ja, bei geschickter Verteilung der Platzdeckchen passen tatsächlich mehr als
500 Mönche daran.
Legt man von den Deckchen je zwei gegenüber und je 250 nebeneinander auf den
Tisch, so passen genau
2 . 250 = 500 Mönche an den Tisch.
![\includegraphics[]{loes51_4_1}](img55.png)
So, wie die Deckchen jetzt liegen, ist natürlich kein Platz für einen weiteren Mönch frei, aber in der Mitte zwischen je vier Deckchen bleibt eine relativ große Fläche ungenutzt.
Legen wir nun die erste Reihe der Deckchen wieder nebeneinander an die eine
Tischkante, die zweite Reihe aber versetzt auf Lücke direkt an die erste
Reihe, so sind die freien Zwischenräume in der Mitte schon kleiner als
eben.
![\includegraphics[]{loes51_4_2d}](img56.png)
Allerdings passen so nur noch 250 + (250 - 1) = 499 Mönche an den Tisch, weil wir diesmal an den Enden ungenutzten Platz haben.
Um jetzt Platz für weitere Mönche zu schaffen, fassen wir die Platzdeckchen zu Dreiergruppen zusammen, wie es in der obigen Abbildung durch die Dreiecke markiert ist. Die erste Dreiergruppe von links verschieben wir an den unteren Tischrand; die Kreise (Deckchen) liegen dann immer noch überschneidungsfrei auf dem Tisch.
![\includegraphics[]{loes51_4_3d}](img57.png)
![\includegraphics[]{loes51_4_3b}](img58.png)
Außerdem ist danach zwischen der Dreiergruppe und dem einzelnen Platz links oben ein kleiner Freiraum, so dass wir die Dreiergruppe auch noch ein wenig nach links schieben können. Dadurch erreichen wir, dass die Mittelpunkte der verschobenen Kreise (ein ganz klein bisschen) weiter links als die ursprünglichen Mittelpunkte sind.
Die zweite Dreiergruppe schieben wir an der oberen Tischkante so weit wie möglich nach links, das heißt so weit, bis sie die beiden rechten Kreise der ersten Dreiergruppe berührt.
Die dritte Dreiergruppe verschieben wir so wie die erste wieder ein Stück schräg nach links unten, die vierte wieder nur nach links. So fortfahrend erhalten wir das folgende Muster:
![\includegraphics[]{loes51_4_5}](img59.png)
Dabei gilt: Sind zwei Mittelpunkte durch eine Strecke miteinander verbunden, so haben sie den Abstand 1, ansonsten ist ihr Abstand größer.
Nun müssen wir nur noch ausrechnen, wie viele dieser Dreiergruppen oder
vielmehr wie viele solcher Streifen der Breite x an den Tisch passen:
![\includegraphics[]{loes51_4_7b}](img60.png)
Da ein Platzdeckchen den Durchmesser 1 hat, hat auch das gleichseitige
Dreieck Seitenlänge 1. Seine Höhe ist dann
![]() , und wir
berechnen
, und wir
berechnen
| z2 = 12 - |
und es folgt, dass der Streifen insgesamt die Breite
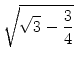
Es gilt
167 . x ![]() 248, 994...< 249, wie der Taschenrechner sagt.
(Da die Abschätzung sehr knapp ist, der Taschenrechner aber nur eine gewisse
Genauigkeit hat, sollte man eigentlich noch mal zu Fuß durch Quadrieren
nachrechnen, dass wirklich
167 . x < 249 gilt!)
Damit können wir 167 Streifen der Breite x auf den ersten
249m
des Tisches unterbringen.
Rechts daneben auf dem freien Meter bleibt noch Platz für den fehlenden
Halbkreis des letzten Streifens und für einen weiteren vollständigen Kreis.
248, 994...< 249, wie der Taschenrechner sagt.
(Da die Abschätzung sehr knapp ist, der Taschenrechner aber nur eine gewisse
Genauigkeit hat, sollte man eigentlich noch mal zu Fuß durch Quadrieren
nachrechnen, dass wirklich
167 . x < 249 gilt!)
Damit können wir 167 Streifen der Breite x auf den ersten
249m
des Tisches unterbringen.
Rechts daneben auf dem freien Meter bleibt noch Platz für den fehlenden
Halbkreis des letzten Streifens und für einen weiteren vollständigen Kreis.
Der Streifen links außen enthält
2![]() Kreise und jeder andere
Streifen enthält
Kreise und jeder andere
Streifen enthält
![]() + 2 +
+ 2 + ![]() = 3 Kreise.
= 3 Kreise.
Insgesamt können auf diese Art und Weise
2![]() + 166 . 3 + 1
+ 166 . 3 + 1![]() = 502
Mönche an dem Tisch speisen.
= 502
Mönche an dem Tisch speisen.
Nachbetrachtungen:
Wir haben hiermit nur bewiesen, dass wir mindestens 502 Mönche an dem Tisch
unterbringen können, aber nicht widerlegt, dass vielleicht sogar 503 Mönche
Platz finden könnten. Ob dies möglich ist oder nicht, wissen wir auch nicht.
Variante:
Ohne Beweis wollen wir noch angeben, dass bei der folgenden Sitzordnung
![\includegraphics[]{loes51_4_9}](img73.png)
Außerdem gilt bei beiden Anordnungen: Haben die beiden Mönche auf der linken
Seite ihren Platz erst einmal fest gewählt, so erhalten wir die angegebenen
Sitzverteilungen, wenn sich die anderen Mönche nacheinander so dazusetzen,
dass der Mittelpunkt ihres Deckchens so weit links wie möglich ist.
So gesehen ergeben sich diese Anordnungen dann doch recht natürlich.
Fußnoten
- ... A.1
- o. B. d. A. = ,,ohne Beschränkung der Allgemeinheit``: Da die Buchstaben a, c bzw. b, d symmetrisch auftreten, dürfen wir uns aussuchen, welcher Bruch der kleinere ist; und trotz unserer willkürlichen Wahl ist der folgende Beweis allgemein gültig.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
