Beispiellösungen zu Aufgabenblatt 60

aktualisiert: 4. Mai 2007

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1


Rebekka muss auf ihrem Weg nach Hause an vier Ampeln vorbei, die (in dieser Reihenfolge) 60 m, 120 m und 80 m auseinander stehen. Alle Ampeln werden zu gleicher Zeit alle 60 Sekunden grün.

Rebekka startet an der ersten Ampel, als diese gerade grün wird, und will mit stets konstanter Geschwindigkeit so laufen, dass sie immer genau dann an der nächsten Ampel ankommt, wenn diese gerade grün wird.

Wie schnell kann sie maximal laufen, damit ihr Plan funktioniert?


Lösung:


Da Rebekka genau dann an der nächsten Ampel ankommen will, wenn diese gerade grün wird, muss sie jeden der drei Abstände zwischen den Ampeln in einem ganzzahligen Vielfachen von 60 Sekunden zurücklegen. Um die maximale Geschwindigkeit zu erhalten, unterteilen wir die drei Strecken in möglichst große, gleich lange Abschnitte, die dann von Rebekka in jeweils 60 Sekunden zurückgelegt werden sollen. Die Maßzahl der gesuchten Länge in Metern ist dann der größte gemeinsame Teiler von 60, 120 und 80. Dieser ist 20, also läuft Rebekka mit einer Geschwindigkeit von $ {\frac{{20}}{{60}}}$$ {\frac{{\mathrm{m}}}{{\mathrm{s}}}}$ = $ {\frac{{1}}{{3}}}$$ {\frac{{\mathrm{m}}}{{\mathrm{s}}}}$ = 1, 2$ {\frac{{\mathrm{km}}}{{\mathrm{h}}}}$.


Aufgabe 2


Die Geschwister Ariadne und Bodo wollen ihre Zimmer vollständig mit roten Teppichfliesen - eine ist in der Abbildung dargestellt - auslegen. Die beiden Zimmer haben, wie im Bild dargestellt, denselben äußeren Grundriss. Allerdings befindet sich in beiden Zimmern je eine Säule quadratischen Querschnitts an unterschiedlicher Stelle, nämlich in Bodos (rechtem) Zimmer um eine quadratische Einheit weiter rechts.

Können beide Räume vollständig mit den Fliesen ausgelegt werden?

Hinweis: Die Fliesen dürfen hierbei auch gedreht, allerdings nicht gespiegelt werden - schließlich soll die rote Teppichseite oben bleiben.

\includegraphics[width=7cm]{raeume.eps}


Lösung:


Ariadnes Zimmer lässt sich vollständig mit den roten Teppichfliesen auslegen. Eine mögliche Anordnung, die dann auch die einzige ist, erhält man, indem man am untersten Zipfel des Zimmers beginnt und im Folgenden jene Fliesen verlegt, die jeweils durch die Form der verbleibenden Fläche eindeutig festgelegt sind. (Eine mögliche derartige Reihenfolge ist durch die Nummerierung in der Skizze unten gegeben.)


Bodos Zimmer hingegen lässt sich nicht vollständig auslegen. Dies kann man sich wie folgt überlegen:

Wir versehen den Boden gedanklich mit einem Schachbrettmuster. Dann bedeckt jede Fliese, unabhängig davon, wie man sie platziert, genau zwei schwarze und zwei weiße Felder. Aufgrund der Position der Säule in Bodos Zimmer gibt es bei einer Färbung wie unten 21 schwarze und nur 19 weiße Felder. Hieraus folgt sofort, dass sich der Boden nicht vollständig auslegen lässt.

Bemerkung 1: Alternativ kann man den zweiten Aufgabenteil auch analog zum ersten Teil lösen: Ähnlich wie in Ariadnes Zimmer sind die Fliesen 10, 9, 8 und 7 in dieser Reihenfolge eindeutig durch die Form des Zimmers festgelegt. Dann lässt sich aber das Feld rechts neben der Säule nicht mehr bedecken.

Bemerkung 2: Man kann sogar zeigen, dass sich ein beliebiges Zimmer mit dieser Art von Fliesen auf höchstens eine Weise auslegen lässt.

\includegraphics[width=120mm]{raeumeloes.eps}


Aufgabe 3


Ein Eisenbahnunternehmen transportiert Container zwischen Adamshafen und Zweibergen: Jeden Tag um 12 Uhr setzen sich in beiden Orten Züge mit dem anderen Ort als Ziel in Bewegung. Für den Transport gibt es zum einen die ,,Standard-Wagen``, die zwei Container tragen können; von ihnen sind immer genügend vorhanden. Dazu gibt es auch Wagen, die nur einen Container tragen können; diese sind relativ teuer, weswegen die Firma davon möglichst wenige bereithalten möchte. Außerdem möchte sie niemals einen unbesetzten Transportplatz in einem Zug haben, weil das unnötig kostet und schlecht für das Image ist. Man darf davon ausgehen, dass bei jedem Transport wenigstens 5 Container befördert werden sollen und dass die genaue Anzahl für jeden Transport eine Stunde vor Beginn feststeht und beiden Verladestellen bekannt ist. Wie viele Wagen, die genau einen Container tragen können, muss die Firma daher mindestens besitzen?

Die Firma hat zudem eine Zweigstelle in den USA - dort ist ja alles etwas größer und es gibt nur Wagentypen, die 5 (Standardwagen) oder 2 (teurer Wagen) Container tragen können, außerdem werden bei jeder Fahrt mindestens 25 Container befördert. Wie lautet die Lösung des entsprechenden Problems für die Zweigstelle in den USA?


Lösung:


In Deutschland braucht das Eisenbahnunternehmen mindestens drei kurze Containerwagen. In den USA sind mindestens zwölf nötig.


Begründung: Zunächst betrachten wie die Situation in Deutschland: In jedem der beiden Bahnhöfe - für die wir kurz A und Z schreiben - muss jeden Morgen mindestens ein kurzer, das heißt: teurer Wagen stehen, damit ein Transport mit einer ungeraden Anzahl an Containern abgefertigt werden kann.

Zwei teure Wagen reichen allerdings nicht: Wenn zum Beispiel von A aus eine gerade Zahl von Containern, von Z aus aber eine ungerade Zahl von Containern transportiert werden soll, muss der kurze Wagen in A stehen bleiben, der von Z geht auf die Reise, so dass auch nach Ankunft der Züge in Z gar kein kurzer Wagen mehr steht.

Jedoch reichen drei kurze Wagen bereits aus: Sie müssen nach dem oben Gesagten so verteilt werden, dass in einem der Bahnhöfe einer und im anderen zwei stehen. Sei A der Bahnhof mit nur einem Wagen. Wenn dann beide Bahnhöfe eine gerade Anzahl an Containern verschicken, darf keiner einen kurzen Wagen im Zug einsetzen. Müssen beide Seiten eine ungerade Anzahl an Containern verschicken, nehmen beide genau einen kurzen Wagen. In beiden Fällen ist die Zahl der Container in A und Z nach Ankunft der Züge dieselbe wie vor der Abfahrt. Wenn schließlich A eine ungerade, Z eine gerade Zahl von Containern losschickt, nimmt A den einen kurzen Wagen, und Z schickt zwei kurze auf die Reise. Das geht, weil ja jeden Tag mindestens fünf Container verschickt werden. Falls umgekehrt A eine gerade, Z eine ungerade Zahl von Containern loszuschicken hat, nimmt A gar keinen kurzen Wagen, und Z nimmt genau einen. In diesen beiden Fällen hat sich nach Ankunft der Züge die Situation umgekehrt: In A stehen zwei kurze Wagen, in Z einer, so dass die Handlungsanweisungen für den nächsten Tag vertauscht werden.

Also kann man die Züge immer bedarfsgerecht zusammenstellen, daher reichen drei kurze Wagen.


In den USA müssen jeden Morgen in jedem Bahnhof mindestens vier kurze Wagen stehen, damit man jede Zahl von Containern versenden kann, denn es gibt offenbar fünf verschiedene Möglichkeiten, welcher Rest beim Teilen der Zahl der Container durch 5 übrig bleibt, und diese Reste 0, 1, 2, 3 und 4 kann man mit 0, 3, 1, 4 und 2 Zwei-Container-Wagen darstellen.

Wenn A 25 und Z 27 Container verschickt, verändert sich die Zahl der kurzen Wagen in A um 5l + 1, dabei ist l eine ganze Zahl. Also kann, wenn man die Anzahl der kurzen Wagen in A als 5m + a mit 0 $ \leq$ a $ \leq$ 4 schreibt, a auch jeden Wert von 0 bis 4 annehmen. Für a = 3 darf jedoch m nicht null sein, denn es müssen ja morgens immer mindestens vier kurze Wagen in jedem Bahnhof sein. Daher müssen dann in A mindestens acht Wagen stehen, gleichzeitig in Z mindestens vier. Also braucht das Eisenbahnunternehmen wenigstens zwölf kurze Wagen.

Diese Zahl ist aber auch schon ausreichend - wir zeigen, dass es immer möglich ist, den Betrieb so zu organisieren, dass in A und Z jeweils mindestens vier Wagen stehen:

Seien in A n kurze Wagen, es stehen in Z daher 12 - n kurze Wagen. Nun sollen von A aus 5k + 2a Container und von Z aus 5j + 2b Container verschickt werden, dabei sei 0 $ \leq$ a, b $ \leq$ 4. Nach dem oben Gesagten ist eine Darstellung der Anzahl in dieser Form immer möglich und außerdem eindeutig.

Wenn die Minimalanzahlen an kurzen Wagen eingesetzt würden, wären in A am nächsten Tag n - a + b und in Z dann 12 - n + a - b kurze Wagen. Wenn beide Zahlen größer gleich 4 sind, kann man die Anzahlen an kurzen Wagen tatsächlich minimal wählen.

Andernfalls gilt: Da die Summe beider Zahlen nach wie vor 12 ist, kann höchstens eine der Zahlen kleiner als 4 sein. Da die Situationen von A und Z vertauscht werden können, dürfen wir im Folgenden annehmen, dass n - a + b $ \leq$ 3 ist. Dann ist n - a + b + 5 = n + (5 - a) + b > n $ \geq$ 4, das heißt, wenn Z nicht b, sondern b + 5 kurze Wagen verschickt, hat A wieder genügend kurze Wagen für den nächsten Tag. Und weil außerdem n - a + b + 5 $ \leq$ 8 ist, ist 12 - n + a - b - 5 $ \geq$ 12 - 8 = 4, also hat auch Z am nächsten Tag genügend Wagen. Bleibt zu zeigen, dass Z überhaupt b + 5 kurze Wagen verschicken kann: In Z stehen nach Voraussetzung 12 - n Wagen, und mit der Vorgabe n - a + b $ \leq$ 3 bzw. äquivalent - n $ \geq$ - 3 - a + b kann man abschätzen: 12 - n $ \geq$ 12 - 3 - a + b = 9 - a + b = 5 + b + (4 - a) $ \geq$ 5 + b. Da immer mindestens 25 Container verschickt werden, hat man auch genügend, um die 2 . (5 + b) $ \leq$ 18 Plätze auf den kurzen Wagen auszufüllen.


Bemerkungen: Wir haben in der Lösung nicht wesentlich benutzt, wie viele Container die kurzen Wagen tragen können; entscheidend war nur, dass die Anzahl teilerfremd zur Anzahl der Container auf einem langen Wagen ist. Das gilt auch im allgemeinen Fall; und wenn man in der Lösung für die USA (sozusagen) fast alle ,,fünf/5`` durch ,,g`` ersetzt, das heißt auch ,,vier/4`` durch ,,g - 1``, ,,drei/3`` durch ,,g - 2``, ,,acht/8`` durch ,,2g - 2`` und ,,zwölf/12`` durch ,,3g - 3``, so erhält man für die verallgemeinerte Aufgabe mit langen Wagen, die g Container, und kurzen Wagen, die h Container tragen, wobei g und h teilerfremd sind, dass das Eisenbahnunternehmen mindestens 3g - 3 kurze Wagen anschaffen muss.


Aufgabe 4


\includegraphics[width=60mm]{peaucellier}

Robin hat auf dem Dachboden ein altes ,,Malwerkzeug`` gefunden. Es besteht aus sechs Stäben, zwei der Länge 10 cm und vier der Länge 6 cm, die beweglich durch Gelenke miteinander verbunden sind (siehe Skizze). Weiterhin befindet sich im Gelenk R eine Abtastspitze, mit der man eine Linie abfahren kann, und im Gelenk G gibt es einen grünen Stift.

Robin probiert das Gerät an der abgebildeten Figur, bestehend aus vier Kreisbogenabschnitten von Kreisen mit Durchmesser 7 cm, aus. Er fährt bei festgehaltenem Ende M also mit der Abtastspitze R die durchgezogene Linie ab, wobei der grüne Stift G eine Kurve auf das Papier malt.

Welche Kurve ist das und welche Länge hat sie?

Hinweis: Man kann bei dieser Aufgabe auch gern das ,,Gerät``, zum Beispiel aus Pappstreifen, nachbauen, und sie auf diese Weise ,,praktisch lösen``!


Lösung:


Da die Lösung einiger Zwischenschritte bedarf, vornweg kurz das Ergebnis: Die entstehende Kurve ist ein Quadrat mit Mittelpunkt M und Seitenlänge $ {\frac{{128}}{{7}}}$ cm. Sein Umfang ist also $ {\frac{{512}}{{7}}}$ cm = 73$ {\frac{{1}}{{7}}}$ cm.

\includegraphics[width=60mm]{peaucellierloes.eps}

Nun zum Beweis: Wir zeigen zunächst folgende Hilfsaussage: Für jede Stellung des Malwerkzeuges gilt

$\displaystyle \overline{{MR}}$ . $\displaystyle \overline{{MG}}$ = a2 - b2,

wobei b allgemein für die Länge der kurzen und a für die Länge der langen Stäbe steht. Das Produkt $ \overline{{MR}}$ . $ \overline{{MG}}$ ist also insbesondere konstant. Zum Beweis dieser Aussage betrachten wir zusätzlich den Schnittpunkt N der Diagonalen in der durch die kurzen Stäbe bestimmten Raute. Dieser halbiert die Diagonalen. Mit dem Satz des Pythagoras folgt dann

a2 = $\displaystyle \overline{{NM}}^{2}_{}$ + $\displaystyle \overline{{NA}}^{2}_{}$        b2 = $\displaystyle \overline{{NR}}^{2}_{}$ + $\displaystyle \overline{{NA}}^{2}_{}$

und somit auch

a2 - b2 = $\displaystyle \overline{{NM}}^{2}_{}$ - $\displaystyle \overline{{NR}}^{2}_{}$ = $\displaystyle \left(\vphantom{\overline{NM} + \overline{NR}}\right.$$\displaystyle \overline{{NM}}$ + $\displaystyle \overline{{NR}}$$\displaystyle \left.\vphantom{\overline{NM} + \overline{NR}}\right)$$\displaystyle \left(\vphantom{\overline{NM} - \overline{NR}}\right.$$\displaystyle \overline{{NM}}$ - $\displaystyle \overline{{NR}}$$\displaystyle \left.\vphantom{\overline{NM} - \overline{NR}}\right)$ = $\displaystyle \overline{{MG}}$ . $\displaystyle \overline{{MR}}$.

Damit ist die Hilfsaussage gezeigt.


Als nächstes zeigen wir, dass der grüne Stift G beim Abtasten eines durch M verlaufenden Kreises mit der Tastspitze R eine Gerade g zeichnet.

Sei dazu k ein Kreis mit Radius r und g eine Gerade, die den Abstand d = $ {\frac{{a^2-b^2-4r^2}}{{2r}}}$ vom Kreis hat. Wir nehmen a2 - b2 - 4r2 $ \geq$ 0 an, was in unserem Beispiel a = 10 cm, b = 6 cm und 2r = 7 cm sicher der Fall ist. Sei M der Punkt des Kreises, der von g den größten Abstand hat. Dann gilt für jeden Punkt G auf g und den Schnittpunkt R von MG mit dem Kreis:

Die beiden rechtwinkligen Dreiecke MSG und MRT (Satz des Thales!) sind ähnlich, und daher ist

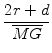$\displaystyle {\frac{{\overline{MR}}}{{2r}}}$ = $\displaystyle {\frac{{2r+d}}{{\overline{MG}}}}$.

Das ist aber äquivalent zu

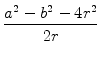
$\displaystyle \overline{{MR}}$ . $\displaystyle \overline{{MG}}$ = 2r(2r + d )= 2r$\displaystyle \left(\vphantom{2r+\frac{a^2-b^2-4r^2}{2r}}\right.$2r + $\displaystyle {\frac{{a^2-b^2-4r^2}}{{2r}}}$$\displaystyle \left.\vphantom{2r+\frac{a^2-b^2-4r^2}{2r}}\right)$ = a2 - b2.

\includegraphics[width=68mm]{peaucellierloes2_2.eps}
Entsprechend der oben gezeigten Hilfsaussage heißt das aber, dass der bei M fixierte Apparat, dessen Tastspitze bei R ist, den Punkt G zeichnet (denn offenbar gibt es auf dem Strahl MR nur genau einen Punkt G, der die Gleichung $ \overline{{MR}}$ . $ \overline{{MG}}$ = a2 - b2 erfüllt).

Also wird beim Abfahren des Kreises tatsächlich die Gerade g gezeichnet.

\includegraphics[width=60mm]{peaucellierloes3_2.eps}

Nun ist der Rest nicht mehr schwer: Die beiden Hilfsaussagen zeigen, dass der grüne Stift beim Abfahren der vier roten Kreisabschnitte mit der Tastspitze vier Strecken zeichnet, aufgrund der Symmetrie der Figur bilden diese sogar die Seiten eines Quadrates - das ist die gesuchte Kurve!

Da in unserem Fall 2r = 7 cm, a = 10 cm und b = 6 cm ist, gilt für den Abstand d der Quadratseite von den kleinen roten Kreisen:

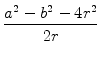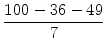d = $\displaystyle {\frac{{a^2-b^2-4r^2}}{{2r}}}$ = $\displaystyle {\frac{{100-36-49}}{{7}}}$cm = $\displaystyle {\frac{{15}}{{7}}}$cm.

Daher hat das grüne Quadrat den Umfang 4(4r + 2d )= $ {\frac{{512}}{{7}}}$ cm. Das ist gleichzeitig die gesuchte Länge der entstehenden Kurve.

Bemerkung: Das Malwerkzeug ist auch als Inversor von Peaucellier bekannt; mit ihm kann man, wie eben gezeigt, die Inversion an einem Kreis praktisch durchführen. Mit Inversion am Kreis, oder auch Kreisspiegelung, bezeichnet man dabei die Abbildung, die für einen gegebenen Kreis mit Mittelpunkt M und Radius $ \rho$ einem beliebigen Punkt R $ \neq$ M denjenigen Punkt G auf dem Strahl MR zuordnet, für den $ \;\stackrel{{}}{{\overline{MG}\cdot\overline{MR}=\rho^2}}\;$ gilt - dies ist also genau die Eigenschaft, die wir oben nachgewiesen haben.

Der Inversionskreis hat in unserem Fall den Radius

$\displaystyle \rho$ = $\displaystyle \sqrt{{a^2-b^2}}$ = 8cm.

Wir haben also gewissermaßen folgende Eigenschaft der Inversion am Kreis bewiesen:
Bei der Inversion an einem Kreis mit Mittelpunkt M werden Kreise, die durch M gehen, auf Geraden abgebildet.

Noch 'ne Bemerkung: Wir haben es uns natürlich nicht nehmen lassen, den Apparat selbst nachzubauen. Einige Impressionen unseres Experiments sieht man in folgenden Bildern.

\includegraphics[width=6cm]{bilda.ps}         \includegraphics[width=6cm]{bildb.ps}

\includegraphics[width=6cm]{bildc.ps}
drucken Zum Ausdrucken als pdf-File oder als ps-File