Beispiellösungen zu Aufgabenblatt 62

aktualisiert: 26. Juli 2007

drucken Zum Ausdrucken als pdf-File oder als ps-File
Aufgabe 1


,,Holladrio!`` jubiliert Musikwissenschaftler Justus Klingtgut, als er zum ersten Mal das kürzlich entdeckte, altertümliche Notenblatt in Händen hält.

Abbildung: Die altertümlichen Noten
\includegraphics[width=10cm]{noten.eps}
Man vermutet, dass unsere Vorfahren, ebenso wie wir heute, für Noten gleicher Länge gleiche Symbole verwendet und innerhalb jedes Kästchens Noten von einer Gesamtlänge von einem Takt (etwa 2 Sekunden) notiert haben. Ein Punkt hinter einem Notenzeichen scheint auch die Notenlänge um 50 Prozent zu verlängern. Die Höhe der Noten könnte durch die Höhe des Symbols im Kästchen angedeutet sein. In Fachkreisen munkelt man, bei obigem Stück handele es sich um ein auch heute noch bekanntes Volkslied.

Finde die Längen der einzelnen Notensymbole!

Zusatz: Für welches andere Musikstück ist der Dichter der zu den obigen Noten gehörenden Textzeilen national bekannt?


Lösung:


Wir betrachten zunächst den vierten Takt. Da dieser aus zwei Kreisen besteht, hat \includegraphics[width=4mm]{kreis} die Länge eines halben Taktes. Im Folgenden verwenden wir die Notensymbole für ihre Längen sowie TE als Bezeichnung für ,,Takteinheit``. Dann gilt für die Takte 1 und 2:

$\displaystyle {\frac{{3}}{{2}}}$$\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ + $\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ + 2$\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ = $\displaystyle {\frac{{7}}{{2}}}$$\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ + $\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ = 1 TE (1)
sowie $\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ + 2$\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ = $\displaystyle {\frac{{1}}{{2}}}$ TE (2)
Aus ([*]) folgt: $\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ = 1 TE - $\displaystyle {\frac{{7}}{{2}}}$$\displaystyle \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ (3)

Einsetzen in ([*]) liefert: $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ + 2 . (1 TE - $ {\frac{{7}}{{2}}}$$ \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$) = $ {\frac{{1}}{{2}}}$ TE, also $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ = $ {\frac{{1}}{{4}}}$ TE.


Mit ([*]) erhält man schließlich: $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ = $ {\frac{{1}}{{8}}}$ TE.

Wegen 1 TE = 2 s ergibt sich $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{kreis}}$ = 1 s, $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{stern}}$ = $ {\frac{{1}}{{2}}}$ s sowie $ \raisebox{-0.5ex}{\includegraphics[width=4mm]{kringel}}$ = $ {\frac{{1}}{{4}}}$ s.


Das gesuchte Stück heißt ,,Alle Vögel sind schon da`` von Hoffmann von Fallersleben, der auch den Text zum Deutschlandlied verfasste.


Aufgabe 2


Kevin steht an einer dreispurigen Autobahn und sieht drei Autos gleichen Typs auf den drei Spuren ankommen. Als sie über eine Fuge fahren, die quer auf der Fahrbahn verläuft, will es der Zufall, dass die Autos fünf Töne in genau gleichen Abständen verursachen, wobei der vierte Ton stärker als die anderen ist. Der Abstand vom ersten zum letzten Ton beträgt genau eine Sechstelsekunde.

Kevin weiß, dass der Achsstand der Autos 2,5 m beträgt, und an die Geschwindigkeitsbeschränkung von 130 km/h haben sich augenscheinlich auch alle Autos in etwa gehalten.

Wie schnell waren die Autos? Und auf welcher Spur fuhr das Auto, das den ersten Ton verursacht hat?


Lösung:


Da der Abstand vom ersten bis zum fünften Ton genau eine Sechstelsekunde beträgt und die Töne in gleichen Zeitabständen zu hören sind, beträgt der Abstand zwischen zwei aufeinanderfolgenden Tönen genau $ {\frac{{ \frac{1}{6} }}{{4}}}$ = $ {\frac{{1}}{{24}}}$ Sekunde.

Sollte ein Auto zwei aufeinanderfolgende Töne verursachen, so muss es die 2, 5 Meter, die der Achsabstand beträgt, in $ {\frac{{1}}{{24}}}$ Sekunde zurücklegen; das entspricht einer Geschwindigkeit von $ {\frac{{2,5}}{{\frac{1}{24}}}}$$ {\frac{{\text{m}}}{{\raisebox{0.25ex}{$\scriptstyle\text{s}$}}}}$ = 60$ {\frac{{\text{m}}}{{\raisebox{0.25ex}{$\scriptstyle\text{s}$}}}}$ = 216$ {\frac{{\text{km}}}{{\text{h}}}}$.

Da sich alle Autos an die Geschwindigkeitsbeschränkung von 130$ {\frac{{\text{km}}}{{\text{h}}}}$ gehalten haben, kann keines der drei Autos zwei aufeinanderfolgende Töne verursacht haben.

Dass der vierte Ton stärker war als die anderen, bedeutet, dass zwei Achsen gleichzeitig über die Fuge gerollt sind. Diese Achsen können keine Vorderachsen gewesen sein, da sonst die zugehörige Hinterachse den fünften Ton hätte erzeugen müssen, was wir gerade ausgeschlossen haben. Also wurde der ,,Doppelton`` von zwei Hinterachsen erzeugt und die zugehörigen Vorderachsen müssen den ersten (Auto 1) und den zweiten Ton (Auto 2) erzeugt haben.

Da es außer dem vierten Ton keine weiteren ,,Doppeltöne`` gab, müssen der dritte und der fünfte Ton vom verbleibenden Auto (Auto 3) verursacht worden sein.


Als Geschwindigkeiten ergeben sich

für Auto 1: v1 = $\displaystyle {\frac{{2,5}}{{\frac{3}{24}}}}$$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 20$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 72$\displaystyle {\frac{{\text{km}}}{{\text{h}}}}$,

für Auto 2: v2 = $\displaystyle {\frac{{2,5}}{{\frac{2}{24}}}}$$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 30$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 108$\displaystyle {\frac{{\text{km}}}{{\text{h}}}}$,

für Auto 3: v3 = $\displaystyle {\frac{{2,5}}{{\frac{2}{24}}}}$$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 30$\displaystyle {\frac{{\text{m}}}{{\text{s}}}}$ = 108$\displaystyle {\frac{{\text{km}}}{{\text{h}}}}$.


Auto 1 hat den ersten Ton verursacht und ist das langsamste gewesen. Wir gehen davon aus, dass kein Auto rechts überholt hat; also muss das Auto auf der rechten Spur den ersten Ton verursacht haben.


Aufgabe 3


Im konvexen Viereck ABCD liegt ein Kreis, der alle vier Seiten des Vierecks berührt. Es ist bekannt, dass | AB| = 2 cm, | BC| = 3 cm und | CD| = 7 cm ist. Außerdem ist der Innenwinkel bei B ein Rechter.

Wie groß ist der Radius des Kreises?


Lösung:


Da ABCD einen Inkreis hat, ist es ein Tangentenviereck, so dass gilt: | AB| + | CD| = | BC| + | DA|. Folglich ist | DA| = 6 cm.

Durch den rechten Winkel bei B ist das Viereck damit eindeutig bestimmt, denn es muss nach Voraussetzung konvex sein, weil sonst nicht alle Seiten den Kreis berühren können.


\includegraphics[width=25mm]{loes62_3a.eps}

Um die genaue Lage von D zu beschreiben, definieren wir einen Hilfspunkt F so, dass AF parallel zu BC und FD parallel zu AB ist. Sei x : = | AF| und y : = | FD|. Es gilt:

x2 + y2 = 62. (4)

Außerdem gilt, die Seite CD betrachtend:

(x - 3)2 + (y + 2)2 = 72. (5)

Subtraktion dieser beiden Gleichungen liefert

6x - 9 - 4y - 4 = - 13    
$\displaystyle \Leftrightarrow$ y = $\displaystyle {\frac{{3}}{{2}}}$x,    

aus ([*]) folgt dann $ {\frac{{13}}{{4}}}$x2 = 36, also (x muss positiv sein) x = $ {\frac{{12}}{{\sqrt{13}}}}$ und y = $ {\frac{{18}}{{\sqrt{13}}}}$.


\includegraphics[width=48mm]{loes62_3b.eps}

Nun können wir uns dem Inkreis zuwenden, wobei die weiteren Bezeichnungen aus der zweiten Skizze ersichtlich werden:

Zum einen gilt

r + v = 2.

Wegen der rechten Winkel sind die Dreiecke RPM und AQR dem Dreieck AFD ähnlich, daher gilt zum anderen:

v . $\displaystyle {\frac{{x}}{{6}}}$ + r . $\displaystyle {\frac{{y}}{{6}}}$ = r.

Einsetzen von r + v = 2 liefert

  (2 - r)·x6 + r·y6 = r
$\displaystyle \Leftrightarrow$ r = $\displaystyle {\frac{{2 \cdot \frac{x}{6}}}{{1 + \frac{x}{6} - \frac{y}{6}}}}$ = $\displaystyle {\frac{{\frac{4}{\sqrt{13}}}}{{1 + \frac{2}{\sqrt{13}} - \frac{3}{\sqrt{13}}}}}$ = $\displaystyle {\frac{{4}}{{\sqrt{13} - 1}}}$ $\displaystyle \approx$ 1, 535.
   


Aufgabe 4


Daniel denkt sich zwei positive, reelle Zahlen a und b, für die a + b = 1 gilt. Dann wählt er positive ganze Zahlen n und m und berechnet

$\displaystyle \left(\vphantom{1-a^m}\right.$1 - am$\displaystyle \left.\vphantom{1-a^m}\right)^{n}_{}$ + $\displaystyle \left(\vphantom{1-b^n}\right.$1 - bn$\displaystyle \left.\vphantom{1-b^n}\right)^{m}_{}$.

Kann dabei ein Wert kleiner als 1 herauskommen?


Lösung:


Zum (eleganten) Beweis dieser Aufgabe denken wir uns ein Feld aus m Zeilen mit je n Kästchen. Und dann betrachten wir das Ganze als Statistik-Aufgabe - auf diese Idee kann man durch die Beziehung a + b = 1 gestoßen werden -, indem jedes einzelne Feld mit der Wahrscheinlichkeit a schwarz und ansonsten, also mit Wahrscheinlichkeit 1 - a = b weiß gefärbt wird.

Für eine fest gewählte Spalte ist dann 1 - am die Wahrscheinlichkeit, dass in dieser Spalte nicht nur schwarze Kästchen sind. Folglich ist (1 - am)n die Wahrscheinlichkeit für die Richtigkeit folgender Aussage:

In keiner Spalte gibt es nur schwarze Kästchen. (6)

Analog ist (1 - bn)m die Wahrscheinlichkeit für die Aussage:

In keiner Zeile gibt es nur weiße Kästchen. (7)

Wenn ([*]) nicht gilt, heißt das, dass es eine Spalte gibt, die nur schwarze Kästchen hat. Da jede Spalte über alle Zeilen geht, hat dann jede Zeile mindestens ein schwarzes Kästchen, also gilt dann ([*]). Daraus folgt, dass die Wahrscheinlichkeit von ([*]) größer gleich der Wahrscheinlichkeit ist, dass ([*]) nicht gilt, also ist

(1 - bn)m $\displaystyle \geq$ 1 - (1 - am)n

oder äquivalent

(1 - am)n + (1 - bn)m $\displaystyle \geq$ 1.

Die gestellte Frage ist also zu verneinen.


Gleichheit gilt übrigens genau dann, wenn ([*]) und ([*]) nicht gleichzeitig wahr sein können. Wenn für m = 1 die Aussage ([*]) wahr ist, gibt es in der (einzigen) Zeile mindestens ein weißes Kästchen. Da dies das einzige Kästchen in seiner Spalte ist, ist dann ([*]) nicht wahr. Daher gilt für m = 1 Gleichheit, analog auch für n = 1. (Das kann man natürlich auch direkt ausrechnen: Für m = 1 formt sich die linke Seite um zu: (1 - am)n + (1 - bn)m = (1 - a)n + (1 - bn) = bn + 1 - bn = 1.)

Wenn m, n $ \geq$ 2 gilt, können hingegen ([*]) und ([*]) gleichzeitig wahr sein: Zum Beispiel kann man das Feld schachbrettartig färben. Daher gilt in diesem Fall echte Ungleichheit.

drucken Zum Ausdrucken als pdf-File oder als ps-File
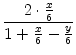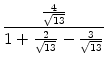