 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.
Aufgabe 1
Für zwei positive reelle Zahlen a und b gelte
![]() = 68.
= 68.
Welche Werte kann dann der Term
![]() annehmen?
annehmen?
Lösung:
Zunächst gilt
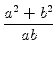 = 68
= 68 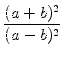 =
= 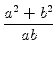 =
=  =
=
Dass die beiden Werte auch wirklich angenommen werden, sieht man zum Beispiel
durch Wahl von b = 1 und
a = 34±![]() : Denn dann gilt
: Denn dann gilt
| a2 + b2 | = 342±68 . |
|
= 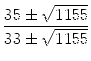 = = 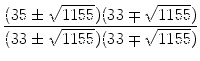 |
||
= 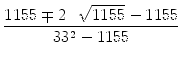 = = 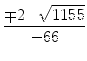 = = 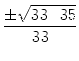 = ± = ± |
Bemerkung: Man findet solche Zahlen a und b durch Auflösen der
Gleichung
![]() = 68 nach einer der beiden Variablen, z. B.
mithilfe der p-q-Formel:
a = b . (34±
= 68 nach einer der beiden Variablen, z. B.
mithilfe der p-q-Formel:
a = b . (34±![]() ). Da der
Radikand positiv ist, erhält man für beliebiges b genau zwei Werte für a
so, dass die Gleichung
). Da der
Radikand positiv ist, erhält man für beliebiges b genau zwei Werte für a
so, dass die Gleichung
![]() = 68 erfüllt ist, und man erhält
somit auch zwei Werte für den Term
= 68 erfüllt ist, und man erhält
somit auch zwei Werte für den Term
![]() . Oben wurde aber bereits
gezeigt, dass dieser Term höchstens die Werte
±
. Oben wurde aber bereits
gezeigt, dass dieser Term höchstens die Werte
±![]() annehmen kann; also werden ebendiese tatsächlich angenommen.
annehmen kann; also werden ebendiese tatsächlich angenommen.
Aufgabe 2
Was ist die kleinste positive ganze Zahl n, für die
2008 . n genau
2008 positive Teiler mehr hat als n selbst?
Lösung:
Die kleinste Zahl mit der geforderten Eigenschaft ist ziemlich groß, nämlich
n = 2244 . 3 . 5 . 7 = 2244 . 105. Sie hat 76 Stellen.
Für eine natürliche Zahl m bezeichnen wir die Anzahl der Teiler von m mit
![]() (m). Diese Anzahl können wir ausrechnen, wenn wir die
Primfaktorzerlegung
(m). Diese Anzahl können wir ausrechnen, wenn wir die
Primfaktorzerlegung
| m = p1e1 . p2e2 . ... . prer |
kennen: Eine Zahl t ist genau dann Teiler von m, wenn sie keine anderen Primfaktoren als m enthält und jeder der vorhandenen Primfaktoren in t nicht öfter als in m vorkommt. Wollen wir also einen Teiler hinschreiben, so haben wir für den ersten Primfaktor p1 die e1 + 1 Möglichkeiten, ihn gar nicht, einmal, zweimal, ... oder e1-mal auszuwählen. Für jede dieser Wahlen haben wir dann für den zweiten Primfaktor p2 genau e2 + 1 Möglichkeiten usw. Die Zahl m hat folglich genau
verschiedene Teiler.
Die Primfaktorzerlegung von 2008 ist
2008 = 23 . 251, damit hat 2008
genau
![]() (2008) = (3 + 1)(1 + 1) = 8 verschiedene Teiler, nämlich
(2008) = (3 + 1)(1 + 1) = 8 verschiedene Teiler, nämlich
| 1, 2, 22 = 4, 23 = 8, 251, 2 . 251 = 502, 22 . 251 = 1004, 23 . 251 = 2008. |
Sei n nun eine beliebige natürliche Zahl. Weil 2008 genau die beiden Primfaktoren 2 und 251 hat, teilen wir auch die Primfaktorzerlegung von n in zwei Teile auf:
| n = |
Dabei dürfen a bzw. b auch gleich null sein, was genau dann passiert, wenn 2 bzw. 251 gar keine Primfaktoren von n sind.
Mit der obigen Formel rechnen wir die Anzahl der Teiler von n und auch von
2008 . n = ![]() 2a+3 . 251b+1
2a+3 . 251b+1![]() .
. ![]() p1e1 . p2e2 . ... . prer
p1e1 . p2e2 . ... . prer![]() aus. Es ist
aus. Es ist
| = (a + 1)(b + 1) . (e1 + 1)(e2 + 1) . ... . (er + 1), | ||
| = (a + 3 + 1)(b + 1 + 1) . (e1 + 1)(e2 + 1) . ... . (er + 1). |
Folglich hat 2008 . n genau
| = |
||
| = (a + 3b + 7) . (e1 + 1) . ... . (er + 1) |
Teiler mehr als n. Die Zahl n erfüllt demnach genau dann die Bedingung der Aufgabenstellung, wenn
gilt. Insbesondere muss (a + 3b + 7) dann einer der acht oben angegebenen Teiler von 2008 sein, dabei ist offensichtlich (a + 3b + 7)
Sei nun n eine Zahl, die diese Bedingungen erfüllt.
Erster Fall: a + 3b + 7 = 8.
Dann ist a = 1, b = 0 und außerdem
(e1 + 1)(e2 + 1)...(er + 1) = 251 eine Primzahl, also r = 1 und
e1 = 251 - 1.
Die Primzahl p1 ![]() 2 ist auf jeden Fall mindestens so groß wie 3, also
ist
n = 21 . 2510 . p1250
2 ist auf jeden Fall mindestens so groß wie 3, also
ist
n = 21 . 2510 . p1250 ![]() 2 . 3250.
2 . 3250.
Zweiter Fall: a + 3b + 7 = 251.
Dann ist
a + 3b = 244 und
2a . 251b ![]() 2a . (23)b = 2a+3b = 2244. Außerdem ist
(e1 + 1) . ... . (er + 1) = 8. Hierfür gibt es wiederum drei Möglichkeiten, abhängig von der Anzahl r
der Primfaktoren:
2a . (23)b = 2a+3b = 2244. Außerdem ist
(e1 + 1) . ... . (er + 1) = 8. Hierfür gibt es wiederum drei Möglichkeiten, abhängig von der Anzahl r
der Primfaktoren:
- r = 1 und
e1 + 1 = 8:
Dann ist
n = 2a . 251b . p1e1
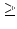 2244 . 37.
2244 . 37.
- r = 2 und
e1 + 1 = 4, e2 + 1 = 2:
Da p1 und p2 verschiedene Primzahlen und ungleich 2 sind, gilt
p13 . p21
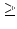 33 . 5. Insgesamt ergibt sich dann
n = 2a . 251b . p1e1 . p2e2
33 . 5. Insgesamt ergibt sich dann
n = 2a . 251b . p1e1 . p2e2 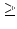 2244 . 33 . 5.
2244 . 33 . 5.
- r = 3 und
e1 + 1 = e2 + 1 = e3 + 1 = 2:
Auch hier sind dann p1, p2 und p3 verschiedene Primzahlen und ungleich
2, so dass diesmal
n = 2a . 251b . p1e1 . p2e2 . p3e3
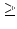 2244 . 3 . 5 . 7 folgt.
2244 . 3 . 5 . 7 folgt.
Dann ist
n = 2a . 251b . p1e1 . ... . prer ![]() 2a(23)b . 1 = 2a+3b
2a(23)b . 1 = 2a+3b ![]() 22 . 251-7 = 2495.
22 . 251-7 = 2495.
Nun vergleichen wir noch die unteren Abschätzungen aus den verschiedenen
Fällen miteinander. Es gilt
| 2 . 3250 | > 2 . (2243 . 3 . 32 . 32) . 32 > 2244 . 3 . 5 . 7 . 1 | |
| 2244 . 37 | = (2244 . 3 . 32 . 32) . 32 > 2244 . 3 . 5 . 7 . 1 | |
| 2244 . 33 . 5 | = 2244 . 3 . 5 . 32 > 2244 . 3 . 5 . 7 | |
| 2495 | = 2244 . 2251 > 2244 . 3 . 5 . 7. |
Alle erlaubten Zahlen sind demnach größer oder gleich n = 2244 . 3 . 5 . 7.
Für diese Zahl
n = 2244 . 3 . 5 . 7 ist r = 3 und es gilt
(a + 3b + 7) . (e1 + 1) . ... . (er + 1) = (244 + 3 . 0 + 7) . (1 + 1)(1 + 1)(1 + 1) = 251 . 8 = 2008. Nach den obigen Überlegungen (bei
Formel (![]() )) erfüllt diese Zahl also tatsächlich die Bedingungen
der Aufgabenstellung und ist somit das gesuchte Minimum dieser Zahlen.
)) erfüllt diese Zahl also tatsächlich die Bedingungen
der Aufgabenstellung und ist somit das gesuchte Minimum dieser Zahlen.
Aufgabe 3
Fliesenleger Ingo benutzt am liebsten Schmuckfliesen, bei denen
3×4
Fliesen schon zusammengesetzt sind. Häufig schafft er es, die zumeist
rechteckigen Grundrisse von Bädern und Küchen damit auszulegen, manchmal muss
er jedoch Fliesen in ihre Einzelfliesen zerteilen. Natürlich fragt er sich
dann, ob er sich
nur dumm angestellt hat oder ob es wirklich nicht anders ging - also: Welche
Rechtecke aus
m×n quadratischen Feldern lassen sich mit Rechtecken der
Größe
3×4 lückenlos und überschneidungsfrei belegen?
Lösung:
Zunächst stellen wir eine notwendige Bedingung an ein Rechteck, das man
überdecken kann: Da jede Schmuckfliese aus 12 Einzelfliesen besteht, muss die
Zahl der quadratischen Felder im Rechteck durch 12 teilbar sein, also:
12| m . n. Da 3 eine Primzahl ist, muss eine der Seitenlängen durch 3 teilbar
sein. Wir können, um weniger Fälle betrachten zu müssen, das Rechteck so
drehen, dass m durch 3 teilbar ist. Bezüglich des Faktors 4 kann man aber
zunächst nur feststellen, dass entweder eine Seitenlänge durch 4 teilbar ist
oder beide Seitenlängen durch 2, aber nicht durch 4 - und diese Fälle
untersuchen wir nun getrennt. Um Missverständnissen vorzubeugen: Wir gehen
davon aus, dass ein m×n-Rechteck m Zeilen und n Spalten hat.
4 teilt n.
Dieser Fall ist einfach: Man kann die Fläche sogar so mit Schmuckfliesen
ausfüllen, dass alle gleichartig angeordnet sind: Man hat
![]() Reihen
zu je
Reihen
zu je
![]() Rechtecken der Größe
3×4, die Schmuckfliesen liegen
alle quer.
Rechtecken der Größe
3×4, die Schmuckfliesen liegen
alle quer.
4 teilt m, also: 12 teilt m.
Wir fangen damit an, den unteren Rand des Rechtecks zu betrachten. Natürlich
ist eine notwendige Bedingung für die Lösung, dass man den unteren Rand
pflastern kann. Das ist in diesem Fall aber auch schon ausreichend:
Überall, wo eine Fliese am unteren Rand quer liegt, werden
![]() - 1
weitere
Fliesen quer darübergelegt, und wo eine Fliese unten hochkant liegt, werden
entsprechend
- 1
weitere
Fliesen quer darübergelegt, und wo eine Fliese unten hochkant liegt, werden
entsprechend
![]() - 1 Fliesen hochkant darübergelegt.
- 1 Fliesen hochkant darübergelegt.
![\includegraphics[width=6cm]{fliesen}](img39.png)
Für alle Zahlen, die durch 3 teilbar sind, trifft dies offenbar zu. Für alle Zahlen größer gleich 4, die beim Teilen durch 3 den Rest 1 lassen, auch, denn sie sind in der Form 4 + k . 3 darstellbar. Ebenso gilt dies für alle Zahlen größer gleich 8, die bei Division durch 3 den Rest 2 haben, da sie sich in der Form 2 . 4 + k . 3 schreiben lassen. Es bleiben die Zahlen 1, 2 und 5 übrig, bei denen man sofort sieht, dass sie sich nicht als Summe von 3en und/oder 4en darstellen lassen.
Ein Beispiel für eine Befliesung in einem Fall, in dem 12 ein Teiler von m ist, sieht man in der Abbildung.
4 teilt weder m noch n.
Wir betrachten die erste Kästchenzeile. Weil n nicht durch 4 teilbar ist,
können nicht alle Fliesen, die in dieser Zeile liegen, quer liegen, und die
Anzahl der hochkant liegenden Fliesen ist nicht null.
Sei a1 diese Anzahl der in der 1. Zeile hochkant liegenden Fliesen. Dann
muss 3a1 bei Division durch 4 denselben Rest wie n lassen - für alle,
die diese Schreibweise noch nicht kennen: Wir notieren das in der Form
3a1 ![]() n mod 4, gesprochen als: ,,3 (mal) a1 ist kongruent zu n
modulo 4``.
n mod 4, gesprochen als: ,,3 (mal) a1 ist kongruent zu n
modulo 4``.
Diese Feststellung gilt für jedes ai, wenn analog ai die Zahl der in der i-ten Zeile hochkant liegenden Fliesen darstellt.
Daher muss die Zahl der in der zweiten Zeile ,,beginnenden`` hochkant
liegenden Fliesen, das
sei b2, durch 4 teilbar sein, denn es ist
b2 = a2 - a1; allgemein ist
bi = ai - ai-1 + bi-4; ebenso auch
b3 = a3 - a2 und
b4 = a4 - a3. Mit der 4. Zeile können erstmals hochkant liegende Fliesen
,,enden``,
und zwar enden genau a1 solche Fliesen. Damit wieder
3a5 ![]() n mod 4
gelten
kann und weil
b2 + b3 + b4
n mod 4
gelten
kann und weil
b2 + b3 + b4 ![]() 0 mod 4 gilt, muss in der fünften
Zeile wieder eine Anzahl b5 an hochkant liegenden Fliesen beginnen, die
insbesondere nicht null
ist (sonst wäre
a5 = b2 + b3 + b4 + b5 durch 4 teilbar), sondern
wiederum mit
3b5
0 mod 4 gilt, muss in der fünften
Zeile wieder eine Anzahl b5 an hochkant liegenden Fliesen beginnen, die
insbesondere nicht null
ist (sonst wäre
a5 = b2 + b3 + b4 + b5 durch 4 teilbar), sondern
wiederum mit
3b5 ![]() n mod 4. Nun geht es
immer so weiter: b6, b7 und b8 müssen durch 4 teilbar sein, b9
darf wiederum nicht durch 4 teilbar sein und so weiter.
n mod 4. Nun geht es
immer so weiter: b6, b7 und b8 müssen durch 4 teilbar sein, b9
darf wiederum nicht durch 4 teilbar sein und so weiter.
Anders betrachtet ergibt sich Folgendes: Weil in der 1. Zeile hochkant liegende Fliesen anfangen, kann das Rechteck nicht eine, zwei oder drei Zeilen haben. Es könnte 4 Zeilen haben. Wenn es mehr als 4 Zeilen hat, kann es weder 5 noch 6 noch 7 Zeilen haben, weil in der 5. Zeile wiederum hochkant liegende Fliesen anfangen. Es könnte aber wieder 8 Zeilen haben. Die Argumentation wiederholt sich immer wieder, und das Ergebnis ist, dass, wenn man das Rechteck vollständig fliesen kann, die Anzahl der Zeilen durch 4 teilbar sein müsste. Das steht aber im Widerspruch zur Voraussetzung!
Das Ergebnis ist also zusammengefasst: Es lassen sich genau alle Rechtecke der Größe m×n fliesen, für die gilt:
- 4| m und 3| n oder
- 3| m und 4| n oder
- 12| m und n ist nicht 1, 2 oder 5 oder
- 12| n und m ist nicht 1, 2 oder 5.
- Jeweils mindestens eine der beiden Zahlen m und n wird durch 3 beziehungsweise 4 geteilt, und keine der Zahlen ist dabei 1, 2 oder 5.
Aufgabe 4
Die Kapitäne Kark, Kerk, Kork und Kurk steuern ihre stolzen (baugleichen)
Raumschiffe durch die unendlichen
Weiten der Galaxis.
![\includegraphics[width=6cm]{raumschiff_bunt_3}](img41.png)
Am Freitagnachmittag starten die vier gleichzeitig zu einem intergalaktischen Treffen: Auf geradem Weg steuern Kark und Kork mit Maximalgeschwindigkeit aufeinander zu, ebenso tun dies Kerk und Kurk. Sobald je zwei aufeinandertreffen, bleiben sie am Treffpunkt stehen. Zeige, dass sich bei dieser Taktik sogar alle vier an einem Ort treffen.
Lösung:
Gegeben haben wir ein Tetraeder
![]()
![]()
![]()
![]() , das aus den vier
Planeten namens
Alpha, Beta, Gamma und Delta gebildet wird, die im Weltall schweben. Die Kark, Kerk,
Kork und Kurk starten jeweils in den Mittelpunkten A, E, O und U der Kanten
, das aus den vier
Planeten namens
Alpha, Beta, Gamma und Delta gebildet wird, die im Weltall schweben. Die Kark, Kerk,
Kork und Kurk starten jeweils in den Mittelpunkten A, E, O und U der Kanten
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() und
und
![]()
![]() .
.
![\includegraphics[width=65mm]{aufgabe4.eps}](img46.png)
Jetzt wenden wir den Strahlensatz in seiner Originalform an:
![]() =
= ![]() =
= ![]() ,
d. h. UO ist gerade halb so lang wie
,
d. h. UO ist gerade halb so lang wie
![]()
![]() .
.
Analog verfahren wir bei den Startpositionen der Kapitäne Kark und Kerk. Es gilt
![]() =
= ![]() =
= ![]() ,
da Kark und Kerk mittig zwischen Alpha und Beta bzw. zwischen Beta und Gamma stationiert sind.
Wieder nach dem umgekehrten Strahlensatz sind die Seiten AE und
,
da Kark und Kerk mittig zwischen Alpha und Beta bzw. zwischen Beta und Gamma stationiert sind.
Wieder nach dem umgekehrten Strahlensatz sind die Seiten AE und
![]()
![]() parallel zueinander, also auch die Seiten AE
und UO. Außerdem gilt nach dem (originalen) Strahlensatz
parallel zueinander, also auch die Seiten AE
und UO. Außerdem gilt nach dem (originalen) Strahlensatz
![]() =
= ![]() =
= ![]() ,
d. h. auch AE ist halb so lang wie
,
d. h. auch AE ist halb so lang wie
![]()
![]() .
.
Damit sind die Seiten UO und AE parallel zueinander und gleich lang. Das Viereck AEOU ist also ein Parallelogramm.
Die in jeweils gegenüberliegenden Eckpunkten dieses Parallelogramms startenden Kapitäne Kark und Kork bzw. Kerk und Kurk fliegen mit derselben Geschwindigkeit aufeinander zu und treffen sich daher in den Mittelpunkten der Diagonalen. Bekanntlich halbieren sich aber in einem Parallelogramm die Diagonalen gegenseitig; daher treffen alle Kapitäne in einem Punkt aufeinander, ohne dass einer von ihnen einen Umweg fliegen müsste.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
