 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.
Aufgabe 1
Es gibt Neues von unseren Piraten der Schwarzen Perle, nachdem sie eine Weile von der Bildfläche verschwunden waren: Sie waren untergetaucht! Käpt'n Sperling ist auf die Idee gekommen, dass man dank Erdkrümmung weniger Strecke mit einem Schiff zurücklegen muss, wenn man zwischendurch etwas taucht, und so wurde die Schwarze Perle zu einem U-Boot umgebaut, dass bis zu 500 m tief gehen kann. (Nebeneffekt: Man entkommt so leichter den Verfolgern!) Zum Vergleich: Der Erdradius beträgt etwa 6366 km.
Auf der Demonstrationsfahrt möchte Käpt'n Sperling den wirklich kürzesten Weg durch den Ärmelkanal zwischen den Häfen von Dover und Calais nehmen, das sind normalerweise 41 km ,,erdgekrümmte`` Strecke. Wie tief wird er dabei eintauchen?
Schließlich geht es auf große Fahrt: Die Mannschaft nimmt sich die (auf dem Wasser gemessen) 6431 km lange Strecke durch den Atlantik von Porto (in Portugal) bis zu - wer hätte es gedacht! - der Insel Tortuga in der Karibik vor. Wie viele Kilometer Strecke kann Sperling durch seine Tauchfähigkeit sparen?
Lösung:
Für die erste Fahrt betrachten wir zunächst einen Durchschnitt der Erdkugel
entlang der Fahrtstrecke Calais-

Dabei sei C Calais und D Dover. Der kürzeste für das U-Boot mögliche Weg
ist dabei die gerade
Strecke CD, sofern ihre tiefste Stelle nicht tiefer als
500m unter dem
Meeresspiegel liegt. Dieser
Punkt ist der Mittelpunkt P der Strecke CD. Die
Mittelsenkrechte zu CD verläuft
durch den Erdmittelpunkt
M. Die Tauchtiefe
im Punkt P ergibt sich dann als Differenz zwischen dem Erdradius
r = 6636km
und | MP|.
Sei ![]() der Winkel
der Winkel
![]() DMC. Dann ergibt sich die trigonometrische
Beziehung
cos
DMC. Dann ergibt sich die trigonometrische
Beziehung
cos![]()
![]()
![]() =
= ![]() .
.
Andererseits gilt, dass sich ![]() zu 360o verhält wie der
Kreisbogen
zu 360o verhält wie der
Kreisbogen
![]() zum Erdumfang 2
zum Erdumfang 2![]() r.
Es gilt also
r.
Es gilt also
![]() =
= ![$ {\frac{{\stackrel{\raisebox{0ex}{$\frown$}}{\raisebox{0ex}[1.05ex]{$\scriptstyle \vert CD\vert$}}\cdot 360^\circ}}{{2\pi r}}}$](img11.png) .
.
Einsetzen in die obige Gleichung ergibt
![$\displaystyle {\frac{{\stackrel{\raisebox{0ex}{$\frown$}}{\raisebox{0ex}[1.05ex]{$\vert CD\vert$}}\cdot 360^\circ}}{{4\pi r}}}$](img13.png)

Die maximale Tauchtiefe ist dann die Differenz zum Erdradius, also ungefähr 33m.
Bemerkung: Die Wegersparnis im Vergleich zur Fahrt auf der Wasseroberfläche beträgt lediglich 7cm.
Wir versuchen nun denselben Ansatz für die Strecke Porto-Tortuga. Einsetzen in die obige Formel mit einer Entfernung von 6431km ergibt dann als maximale Tauchtiefe

Um den kürzesten möglichen Weg zu finden, betrachten wir - ähnlich wie oben - einen Durchschnitt der Erde entlang der Strecke von Porto (P) nach Tortuga (T). Dazu zeichnen wir noch einen inneren Kreis um den Erdmittelpunkt M mit Radius 6365, 5km, der die maximale Tauchtiefe angibt.
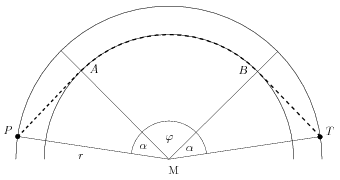
Gesucht ist nun der kürzeste Weg von P nach T innerhalb des äußeren
Kreisringes. Anschaulich gesprochen ist dies der Weg, den ein Gummiseil
beschreibt, wenn man es von P nach T spannt und wenn der Meeresboden
überall exakt 500 Meter unter der Wasseroberfläche liegt.
Mathematisch ausgedrückt heißt das, dass man am Anfang und am
Ende des Weges jeweils auf einer Tangente durch P
bzw. T an den inneren Kreis (mit Tangentialpunkten A bzw. B)
fährt. Der optimale Weg zwischen den Tangentialpunkten ist
der Kreisbogen
![]() .
.
Da in A und B jeweils ein rechter Winkel
![]() PAM bzw.
PAM bzw.
![]() MBT
vorliegt, ergibt sich aus dem Satz des Pythagoras
MBT
vorliegt, ergibt sich aus dem Satz des Pythagoras
| | PA| = | TB| | = |
|
| = |
Die beiden Dreiecke PAM und TBM sind also kongruent und wir bezeichnen den
Winkel
![]() AMP bzw.
AMP bzw.
![]() TMB als
TMB als ![]() .
.
Sei
![]() =
= ![]() BMA. Dann gilt
BMA. Dann gilt
![]() =
= ![]() .
.
Es folgt mit
sin![]() =
= ![]() =
= ![]() , also
, also
![]() = arcsin
= arcsin![]() , dass
, dass
 - 2 arcsin
- 2 arcsin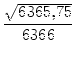
Andererseits ist
![]() =
= ![$ {\frac{{\stackrel{\raisebox{0ex}{$\frown$}}{\raisebox{0ex}[1.05ex]{$\scriptstyle
\vert AB\vert$}}}}{{2\pi\cdot
(r-0,5)}}}$](img37.png)
![]()
![]() =
= ![]() .
.
Einsetzen von ![]() ergibt
ergibt
=  - 2 arcsin - 2 arcsin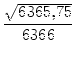 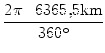 |
||
| = 6270, 9319km. |
Der Gesamtweg hat dann die Länge
| PA| + ![]() + | BT| = 6270, 9319km + 2 .
+ | BT| = 6270, 9319km + 2 . ![]() km = 6430, 5033km. Die Wegersparnis beträgt somit
ca.
497m.
km = 6430, 5033km. Die Wegersparnis beträgt somit
ca.
497m.
Bemerkung: Bei den Berechnungen in dieser Lösung kommt man in die Nähe
der Rechengenauigkeit eines Taschenrechners: Im ersten Aufgabenteil zum
Beispiel wird vom Erdradius eine ähnlich große Zahl (| MP|) abgezogen. Damit
werden am Anfang viele ,,gültige`` (d. h. nicht gerundete) Stellen
ausgelöscht, und im Ergebnis sind nur wenige Stellen wirklich genau
gerechnet. Auch die Berechnungen im zweiten Aufgabenteil sind aus ähnlichem
Grund teilweise empfindlich gegen Rundungen. Am besten rechnet man in solchen
Fällen mit einer ,,kompletten Formel``, um Rundungen zwischendurch
zu vermeiden. Wenn Dover und Calais nur wenige Meter auseinander liegen
würden, reicht auch das (auf normalen Taschenrechnern) nicht aus; man muss
dann nach
anderen Tricks suchen. (Für Eingeweihte: Mithilfe von Additionstheoremen kann
man die Formel hier in eine besser berechenbare umstellen.)
Aufgabe 2
Welche fünfstelligen Zahlen, bei denen keine Ziffer Null ist, haben die
Eigenschaft, dass ihre letzte Ziffer
die aus den letzten beiden Ziffern gebildete Zahl teilt, dass die aus den
letzten beiden Ziffern gebildete Zahl die aus den letzten drei Ziffern
gebildete Zahl teilt, dass die aus den letzten drei Ziffern gebildete Zahl die
aus den letzten vier Ziffern gebildete Zahl teilt und schließlich dass die
aus den letzten vier Ziffern gebildete Zahl die gesamte Zahl selbst teilt?
Lösung:
Es gibt genau drei Lösungen: 53125, 91125 und 95625.
Beweis: Sei die fünfstellige Zahl abcde eine Lösung der Aufgabe. Dann teilt
insbesondere bcde die Zahl abcde und damit auch die Zahl
abcde - bcde = a0000 = a . 24 . 54. Da a eine Ziffer (ungleich Null) sein soll,
bedeutet das, dass bcde
ein Produkt von einem Faktor kleiner gleich 9 (ein Teiler von a), einer
Zweierpotenz 2i mit i ![]() 4
und einer Fünferpotenz 5j mit j
4
und einer Fünferpotenz 5j mit j ![]() 4 sein muss. Außerdem ist nach
Voraussetzung e
4 sein muss. Außerdem ist nach
Voraussetzung e ![]() 0, daher ist bcde nicht durch 10 teilbar oder anders
gesagt: enthält nicht gleichzeitig Primfaktoren 2 und 5.
0, daher ist bcde nicht durch 10 teilbar oder anders
gesagt: enthält nicht gleichzeitig Primfaktoren 2 und 5.
Wäre bcde nicht durch 5 teilbar, so wäre damit
bcde ![]() a . 24
a . 24 ![]() 9 . 16 = 144 < 1000 im Widerspruch zur Forderung, dass auch b
9 . 16 = 144 < 1000 im Widerspruch zur Forderung, dass auch b ![]() 0
gelten soll. Also ist
bcde =
0
gelten soll. Also ist
bcde = ![]() . 5j mit j
. 5j mit j ![]() 4 und einem
Teiler
4 und einem
Teiler ![]() von a, und weil
9 . 52 = 225 < 1000 ist, ist j
von a, und weil
9 . 52 = 225 < 1000 ist, ist j ![]() 3. Wegen
8 . 53 = 1000 kommt für den
Fall j = 3 nur die Wahl
3. Wegen
8 . 53 = 1000 kommt für den
Fall j = 3 nur die Wahl
![]() = 9 und damit auch a = 9 infrage. Es ist
9 . 125 = 1125 eine Zahl
ohne Nullen, also ist 91125 ein Lösungskandidat. Wegen
1125 . 81 = 91125,
125 . 9 = 1125,
25 . 5 = 125 und
5 . 5 = 25 ist
tatsächlich 91125 eine Lösung.
= 9 und damit auch a = 9 infrage. Es ist
9 . 125 = 1125 eine Zahl
ohne Nullen, also ist 91125 ein Lösungskandidat. Wegen
1125 . 81 = 91125,
125 . 9 = 1125,
25 . 5 = 125 und
5 . 5 = 25 ist
tatsächlich 91125 eine Lösung.
Weitere Lösungen kann es nur für den Fall j = 4 geben, es ist dann also
bcde = ![]() . 625, wobei
. 625, wobei ![]() wiederum ein Teiler von a und
ungerade sein
muss.
1 . 625 = 0625 liefert eine Null;
3 . 625 = 1875 führt
genauso wie
7 . 625 = 4375 zu keiner Lösung, weil offenbar 875 kein
Teiler von 1875 (bzw. 1000) ist (auch nicht 75 ein Teiler von 875) und etwas
weniger klar 375 kein Teiler von 4375 ist (denn 3 teilt 375, aber nicht 4000).
Wählt man
wiederum ein Teiler von a und
ungerade sein
muss.
1 . 625 = 0625 liefert eine Null;
3 . 625 = 1875 führt
genauso wie
7 . 625 = 4375 zu keiner Lösung, weil offenbar 875 kein
Teiler von 1875 (bzw. 1000) ist (auch nicht 75 ein Teiler von 875) und etwas
weniger klar 375 kein Teiler von 4375 ist (denn 3 teilt 375, aber nicht 4000).
Wählt man
![]() = 5, so ist bcde = 55, damit muss, weil
a0000 = 16 . 54 . a ist, a auch durch 5 teilbar sein. Da a eine Ziffer
ungleich Null sein soll, bleibt als einzige Möglichkeit a = 5. Wegen
53125 = (16 + 1) . 3125 (wie konstruiert) und
3125 = 25 . 125 ist 53125 eine
weitere Lösung.
= 5, so ist bcde = 55, damit muss, weil
a0000 = 16 . 54 . a ist, a auch durch 5 teilbar sein. Da a eine Ziffer
ungleich Null sein soll, bleibt als einzige Möglichkeit a = 5. Wegen
53125 = (16 + 1) . 3125 (wie konstruiert) und
3125 = 25 . 125 ist 53125 eine
weitere Lösung.
Wählt man schließlich
![]() = 9, so ist also
bcde = 54 . 9, und damit
muss ebenso a = 9 gewählt werden. Es ist
9 . 625 = 5625, und wegen
95625 = (16 + 1) . 5625 und bekanntermaßen
625 = 25 . 25 ist 95625
eine dritte und die letzte Lösung der Aufgabe.
= 9, so ist also
bcde = 54 . 9, und damit
muss ebenso a = 9 gewählt werden. Es ist
9 . 625 = 5625, und wegen
95625 = (16 + 1) . 5625 und bekanntermaßen
625 = 25 . 25 ist 95625
eine dritte und die letzte Lösung der Aufgabe.
Ein paar weiterführende Bemerkungen (ohne Beweise):
Wie man vielleicht schon am Beweis erkannt hat, ist die Forderung, dass keine
der Ziffern eine Null sein soll, eine wesentliche Forderung. Lässt man Nullen
zu, so erhält man etliche weitere Lösungen.
Wenn man schon Nullen zulässt, kann man auch gleich die Aufgabe für beliebige Stellenzahlen untersuchen. Man erhält dann automatisch unendlich viele Lösungen, denn man kann aus einer Lösung weitere erzeugen, indem man zwischen der ersten und der zweiten Ziffer beliebig viele Nullen einfügt. Auch am Ende kann man beliebig viele Nullen anhängen.
Interessant sind nach dem oben Gesagten nur noch Lösungen, bei denen die erste Ziffer keine Null ist (das ist in jedem Fall vernünftig), die letzte Ziffer ebenso keine Null ist und bei denen die zweite Ziffer nur dann eine Null ist, wenn sich keine Lösung ergibt, wenn man die Null weglässt. Wir wollen eine solche Lösung als wesentliche Lösung bezeichnen. Man kann schließlich zeigen: Es gibt genau 148 wesentliche Lösungen. Darunter sind 9 einstellige, 41 zweistellige, 30 drei-, 25 vier-, 17 fünf-, 20 sechs-, 5 siebenstellige Lösungen und als längste eine achtstellige Lösung. Sie lautet 90703125 und zeigt, dass die etwas umständlich anmutende Formulierung oben zur zweiten Ziffer einer wesentlichen Lösung nötig ist, denn 703125 ist 9 . 57, sodass die nächste Ziffer ungleich Null, die ja eine Neun sein muss, weil keine Zehnerpotenz durch drei teilbar ist, erst auf der 107-er-Stelle stehen kann.
Wesentliche Lösungen ohne Nullen gibt es immerhin 90, und die größten unter ihnen sind genau die drei fünfstelligen. Alle 14 vierstelligen Lösungen sind - das kann man genau wie in der Lösung oben zeigen - bis auf eine Ausnahme (9225) durch 125 teilbar. Auf die Ziffern 7 oder 9 enden unter den wesentlichen Lösungen ohne Null nur die trivialen Lösungen 7, 9, 77 und 99.
Die meisten Nullen in einer wesentlichen Lösung haben die Lösungen a000064 mit a = 1, 3, 5, 7 oder 9.
Interessant wäre sicherlich noch die Untersuchung des Problems in anderen Stellenwertsystemen - aber das würde den Rahmen hier sprechen, also überlassen wir es dem geneigten Leser, dies selbst zu tun.
Aufgabe 3
Beim Abheften des folgenden Gleichungssystems ist es leider an den falschen
Stellen gelocht worden ...
| x + 4y | = |
|
| 2x |
= |
Die fehlenden Zahlen werden noch gefunden:
Lösung:
Anstelle der Löcher setzen wir Variablen ein.
Das Gleichungssystem
soll nach Voraussetzung eindeutig lösbar sein. Würde man a2 = 8 wählen, wäre die linke Seite der zweiten Gleichung das Doppelte der linken Seite der ersten Gleichung. Das heißt, dass das Gleichungssystem entweder gar nicht lösbar ist (und zwar, wenn a3
Wir berechnen nun allgemein die Lösungen des Gleichungssystems; die Umformungen sind in jedem Fall Folgerungen aus (wenn nicht sogar Äquivalenzen zu) den vorigen Gleichungen.
Zunächst bilden wir
2 . (![]() ) - (
) - (![]() ):
):
| (8 - a2)y | = 2a1 - a3 | |
| y | = 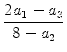 . . |
Das Teilen durch 8 - a2 ist allgemein möglich, weil wir ja gerade a2
Dies in (![]() ) eingesetzt, ergibt zusammen mit der Voraussetzung, dass
bei einer Lösung der Aufgabe x positiv ist,
) eingesetzt, ergibt zusammen mit der Voraussetzung, dass
bei einer Lösung der Aufgabe x positiv ist,
| 0 < x | = a1 - 4y | |
= a1 - 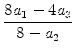 . . |
Für a2 = - 4 und auch für a2 = - 8 gilt 8 - a2 > 0. Damit folgt aus der Ungleichung weiter
| 8a1 - a1a2 - 8a1 + 4a3 | > 0 | |
| - a1a2 + 4a3 | > 0 | |
| a1a2 - 4a3 | < 0. |
Angenommen, a2 = - 4 führt zu einer Lösung. Dann ist
| -4a1 - 4a3 | < 0 | |
| a1 + a3 | > 0. |
Dies führt aber zu einem Widerspruch, da a1 + a3 die Summe von -8 und 8, also null ist. Also muss gelten: a2 = - 8. Damit ergibt sich
| -8a1 - 4a3 | < 0 | |
| 2a1 + a3 | > 0 | |
| 2a1 | > - a3. |
Diese Ungleichung ist nur erfüllt für a1 = 8 und a3 = - 4 (und nicht umgekehrt).
Eine Probe bestätigt die Lösung.
Das korrekte Gleichungssystem sieht also so aus:
| x + 4y | = + 8 | (3) |
| 2x - 8y | = - 4 | (4) |
und hat die Lösungen x = 3, y =
Aufgabe 4
Das siebenköpfige Korrespondenzzirkelteam sitzt im Kreis und vertreibt sich
die Zeit mit folgendem Spiel:
Zu Beginn hat jeder eine zufällige Anzahl von Äpfeln vor sich liegen, jedoch nicht mehr als 20. In der Mitte der Runde befindet sich außerdem ein sehr großer Apfelvorrat. Ein Spielzug besteht nun darin, dass zunächst alle Spieler mit einer ungeraden Anzahl von Äpfeln einen Apfel vom Vorrat nehmen. Danach geben alle Spieler gleichzeitig die Hälfte ihrer Äpfel an ihren jeweils rechten Sitznachbarn weiter.
Das Spiel ist beendet, sobald der Vorratsberg aufgebraucht ist.
Zeige, dass das Spiel niemals endet, wenn man den Vorrat nur groß genug (aber endlich) wählt.
Finde - abhängig von der Anfangssituation - einen möglichst kleinen Vorrat, der dafür ausreicht, dass das Spiel nicht endet.
Lösung:
Erster Teil: Das Spiel endet niemals.
Zu Beginn des Spiels hat laut Aufgabenstellung kein Spieler mehr als 20
Äpfel vor sich liegen.
Das gilt aber auch nach der ersten Hälfte des Spielzuges
(,,füge einen Apfel hinzu, falls deine Anzahl ungerade ist``)
noch, denn 20 ist eine gerade Zahl.
Sei nun a die Anzahl an Äpfeln eines Spielers X und sei b die Anzahl der
Äpfel seines linken Nachbarn (jeweils nach der ersten Hälfte des Zuges).
Aufgrund der letzten Überlegung gilt
a, b ![]() 20.
In der zweiten Hälfte des Zuges gibt der Spieler X die Hälfte seiner Äpfel
fort, behält also insbesondere die (andere) Hälfte seiner eigenen Äpfel, und erhält gleichzeitig die Hälfte der Äpfel seines linken Nachbarn, sodass er nach dem Spielzug genau
20.
In der zweiten Hälfte des Zuges gibt der Spieler X die Hälfte seiner Äpfel
fort, behält also insbesondere die (andere) Hälfte seiner eigenen Äpfel, und erhält gleichzeitig die Hälfte der Äpfel seines linken Nachbarn, sodass er nach dem Spielzug genau
![]() +
+ ![]() =
= ![]() Äpfel besitzt.
Mit der obigen Abschätzung für a, b folgt für diese Anzahl
Äpfel besitzt.
Mit der obigen Abschätzung für a, b folgt für diese Anzahl
![]()
![]()
![]() = 20.
= 20.
Folglich hat auch nach dem kompletten Spielzug jeder der Spieler höchstens 20 Äpfel vor sich liegen. Dies gilt auch nach jedem weiteren Spielzug.
Zusammen brauchen die sieben Spieler also höchstens 7 . 20 = 140 Äpfel; und spätestens, wenn jeder 20 Äpfel vor sich liegen hat, werden keine weiteren Äpfel aus dem Vorrat benötigt und das Spiel kann endlos weitergehen.
Zweiter Teil: Wie groß muss der Vorrat sein?
Diese Anzahl ist sehr von der gegebenen Anfangssituation abhängig und auch
uns noch nicht vollständig bekannt.
Eine erste Begrenzung der Anzahl haben wir im ersten Teil schon gesehen:
Insgesamt werden nie mehr als 140 Äpfel benötigt, und zwar in der Anzahl
der zu Beginn vor den Spielern liegenden Äpfel und im Vorrat zusammen.
Diese Abschätzung können wir aber noch verbessern, indem wir die Schranken aus dem ersten Teil exakter wählen: Seien x1, x2,..., x7 die Anzahlen der zu Beginn vor den einzelnen Spielern liegenden Äpfel. Sei M das Maximum dieser Anzahlen. Falls M gerade ist, so setzen wir m : = M, und anderenfalls - also wenn M ungerade ist - setzen wir m : = M + 1. In beiden Fällen ist dann m eine gerade Zahl und keiner der Spieler hat zu Beginn mehr als m Äpfel.
Da m wiederum gerade ist, ergibt sich wie oben, dass nach der ersten Hälfte
des Zuges kein Spieler mehr als m Äpfel hat. Und auch nach der zweiten
Hälfte des Zuges gilt (mit den entsprechenden Bezeichnungen wie oben) für
die Apfelanzahl eines jeden Spielers:
![]()
![]()
![]() = m.
= m.
Es werden also insgesamt höchstens 7 . m Äpfel benötigt. Und da bereits x1 + x2 +...+ x7 Äpfel von Anfang an vor den Spielern liegen, braucht der Vorrat höchstens 7 . m - (x1 + x2 +...+ x7) Äpfel zu enthalten.
Es gibt viele nichttriviale Beispiele, in denen diese Abschätzung scharf ist: Zum Beispiel führt die Startsituation (5, 19, 19, 13, 0, 0, 0) nach 22 Zügen dazu, dass alle Spieler 20 Äpfel haben.
Jedoch gibt es auch Beispiele, in denen auch die zweite Abschätzung nicht die
beste ist:
Gibt es etwa nur zwei Spieler, die zu Beginn 4 bzw. 8 Äpfel haben,
so benötigen sie gar keinen zusätzlichen Vorrat, denn: Beide Anzahlen sind
gerade, und nach dem ersten Zug haben sie
![]() = 6 bzw.
= 6 bzw.
![]() = 6 Äpfel, sodass auch nach allen
folgenden Zügen jeder der beiden Spieler genau 6 Äpfel besitzt und kein
zusätzlicher Apfel benötigt wird.
= 6 Äpfel, sodass auch nach allen
folgenden Zügen jeder der beiden Spieler genau 6 Äpfel besitzt und kein
zusätzlicher Apfel benötigt wird.
Zusatz: Am ,,Ende`` haben alle gleich viele Äpfel.
Wir haben bislang nur gezeigt, dass immer nur ein endlicher Vorrat nötig
ist. Damit ist nach Aufgabenstellung das Spiel bei genügend großem Vorrat
niemals zu Ende. Aber, wie eine Einsenderin richtig schrieb: ,,Die Spieler
werden irgendwann sowieso aufhören, wenn sie wieder an die Arbeit müssen oder
keine Lust mehr haben.``
Es drängt sich da noch die Frage auf, ab wann das Spiel langweilig wird. Sicherlich dann, wenn alle die gleiche gerade Anzahl Äpfel haben, denn dann kann sich nichts mehr ändern. Dies wird tatsächlich immer eintreten. Den Beweis dazu wollen wir nur andeuten: Man kann zeigen, dass Folgendes gilt: Sei die Situation gegeben, dass nicht alle die gleiche Anzahl an Äpfeln haben. Wir betrachten speziell die kleinste vorkommende Zahl an Äpfeln auf einem Haufen. Dann ist nach dem nächsten Schritt entweder diese Minimalzahl größer geworden oder aber die Zahl der Spieler, die einen Haufen mit der Minimalzahl haben, ist kleiner geworden. Damit verändert sich die Spielsituation mit jedem Zug wesentlich, bis der Zustand erreicht wird, dass alle Spieler die gleiche gerade Anzahl an Äpfeln vor sich haben.
Weitere Bemerkungen.
Das Spiel mit maximal 20 Äpfeln endet nach spätestens 22 Runden. Und das
Beispiel
oben mit der Startsituation
(5, 19, 19, 13, 0, 0, 0) gibt den maximal
benötigten Vorrat an: 84 Äpfel.
Wenn man zu Beginn mehr Äpfel zulässt, kann man den maximal benötigten Vorrat noch deutlich erhöhen: Die Startsituation (0, 97, 99, 93, 99, 99, 60) beispielsweise führt nach 30 Runden zum Endstand, dass alle Spieler 100 Äpfel haben, man braucht also einen Vorrat von 153 Äpfeln. Ob dies das Maximum ist, wissen wir nicht, unser Computer rechnet noch ...
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
