 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.
Aufgabe 1
Käpt'n Jakob Sperling und seine Piraten der Schwarzen Perle haben in
ihrer letzten Seeschlacht schwere Verluste erlitten. Daher landen sie auf
Tortuga und suchen nach Ersatz für ihre verletzten Kameraden.
Da jedoch alle Piraten sehr abergläubisch sind, muss die Anzahl der neuen
Männer gewisse Piratenregeln erfüllen: Sie muss eine Primzahl und ein
Palindrom sein und die Anzahl ihrer Ziffern muss gerade sein.
Wie viele neue Mannschaftsmitglieder kann Käpt'n Jakob höchstens anheuern?
Hinweis: Ein Palindrom ist eine Zahl, die sich nicht ändert, wenn man ihre Ziffernreihenfolge umkehrt.
Lösung:
Um all diese Vorgaben zu erfüllen, muss Käpt'n Jakob genau 11 neue Männer anheuern.
Sei x ein Palindrom mit einer geraden Anzahl von Stellen, d. h. x habe
2m Stellen (m ist eine natürliche Zahl) und die Form
Dann steht a1 an der 1. und 2m-ten, a2 an der 2. und (2m - 1)-ten, ... sowie am an der m-ten und (m + 1)-ten Stelle von x. Also kommt jedes aii = 1,..., m) einmal an einer ungeraden und einmal an einer geraden Stelle vor. Bilden wir nun die alternierende Quersumme AQ(x) von x, wird daher jedes ai einmal addiert und einmal subtrahiert. Wir erhalten also:
| AQ(x) | = a1 - a2 + a3 -...±am |
|
| = (a1 - a1) - (a2 - a2) + (a3 - a3) -...±(am - am) = 0. |
Eine Teilungsregel besagt, dass eine Zahl genau dann durch 11 teilbar ist, wenn ihre alternierende Quersumme durch 11 teilbar ist. Da 0 durch 11 teilbar ist, ist also auch x durch 11 teilbar.
Fordert man schließlich wie in der Aufgabenstellung, dass x eine Primzahl sein soll, folgt somit x = 11 als einzige Lösung des Problems.
Beweis der Teilbarkeitsregel für 11:
Eine Zahl 11...1, die aus einer geraden Anzahl Einsen besteht, ist durch 11 teilbar:
Für reine Zehnerpotenzen mit einem geraden Exponenten 2k gilt
| 102k | = 1 = = 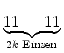 0 - 0 - 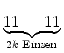 + 1 + 1 |
|
| = 11 . 10t - 11 . t + 1 = 11 . (10 - 1)t + 1 = 11 . q + 1 |
mit den natürlichen Zahlen t wie in (
| 102k+1 | = 1 = = 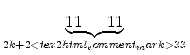 - - 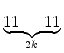 0 - 1 0 - 1 |
|
| = 11 . t - 11 . 10s - 1 = 11 . (t - 10s) - 1 = 11 . q - 1 |
mit den natürlichen Zahlen t, s wie in (
Sei nun
y = bnbn-1...b2b1 eine beliebige n-stellige
Zahl mit den Ziffern
bi ![]() {0, 1,..., 9}. Die
Ziffernschreibweise (im Dezimalsystem) bedeutet, dass
{0, 1,..., 9}. Die
Ziffernschreibweise (im Dezimalsystem) bedeutet, dass
| y = bn . 10n-1 + bn-1 . 10n-2 +...+ b2 . 101 + b1 . 100 |
ist. Versehen wir die Zahlen q in den obigen Zerlegungen noch mit einem Index, etwa 102k = 11 . q2k + 1 und 102k+1 = 11 . q2k+1 - 1, so ergibt sich, wenn wir von rechts anfangen zu summieren:
| y | = b1 + (11q1b2 - b2) + (11q2b3 + b3) +...+ (11qn-1bn±bn) | |
| = (b1 - b2 + b3 -...±bn) + 11 . (q1b2 + q2b3 +...+ qn-1bn). |
Da der letzte große Summand ein Vielfaches von 11 ist, ist die Zahl y genau dann durch 11 teilbar, wenn der erste Summand durch 11 teilbar ist.
Dieser erste Summand ist aber genau die alternierende Quersumme AQ(y) = b1 - b2 + b3 -...±bn von y, womit die Teilbarkeitsregel bewiesen ist.
Aufgabe 2
Eine Lösung der Gleichung
x2 - 6x + 7 = 0 hat an ihrer 2007. Nachkommastelle
die Ziffer 8. Welche Ziffer hat die andere Lösung in ihrer
2007. Nachkommastelle?
Lösung:
Es sind
3 + ![]() und
3 -
und
3 - ![]() die beiden Lösungen der Gleichung
x2 - 6x + 7 = 0.
die beiden Lösungen der Gleichung
x2 - 6x + 7 = 0.
Sei a diejenige Lösung mit der Ziffer 8 in ihrer 2007. Nachkommastelle und b die andere.
Offensichtlich gilt a + b = 6.
Außerdem sind a und b beide nicht negativ und haben als irrationale Zahlen unendlich viele von Null verschiedene Nachkommastellen. Wir schreiben:
| a | = a0, a1a2... | |
| b | = b0, b1b2... |
mit den Ziffern ai, bi
Angenommen, es wäre
a0 + b0 ![]() 6, dann wäre a + b > 6, da a und b von
Null verschiedene Nachkommastellen besitzen. Außerdem wäre a + b < 6 im Falle
von
a0 + b0 < 5, da nicht alle Nachkommastellen Neunen sind - zumindest ist
a2007 = 8.
6, dann wäre a + b > 6, da a und b von
Null verschiedene Nachkommastellen besitzen. Außerdem wäre a + b < 6 im Falle
von
a0 + b0 < 5, da nicht alle Nachkommastellen Neunen sind - zumindest ist
a2007 = 8.
Es folgt a0 + b0 = 5 und somit 0, a1a2a3...+ 0, b1b2b3...= 1.
Nun betrachten wir die erste Nachkommastelle.
Wir nehmen an, es wäre
a1 + b1 ![]() 10.
Dann wäre
0, a1a2a3...+ 0, b1b2b3...> 1, da es weitere von Null
verschiedene Nachkommastellen gibt.
Andererseits wäre
0, a1a2a3...+ 0, b1b2b3...< 1,
falls
a1 + b1 < 9 wäre.
Es folgt, dass
a1 + b1 = 9 ist, und somit muss
0, 0a2a3...+ 0, 0b2b3...= 0, 1 gelten.
10.
Dann wäre
0, a1a2a3...+ 0, b1b2b3...> 1, da es weitere von Null
verschiedene Nachkommastellen gibt.
Andererseits wäre
0, a1a2a3...+ 0, b1b2b3...< 1,
falls
a1 + b1 < 9 wäre.
Es folgt, dass
a1 + b1 = 9 ist, und somit muss
0, 0a2a3...+ 0, 0b2b3...= 0, 1 gelten.
Induktiv kann man nun schließen, dass
ai + bi = 9 für alle i ![]() 1
gilt.
1
gilt.
Mit a2007 = 8 folgt also: b2007 = 9 - a2007 = 1.
Aufgabe 3
Ein Billardtisch ist 128 cm lang und 88 cm breit. An den vier Ecken hat
er je ein viertelkreisförmiges Loch, durch das eine Billardkugel mit 5 cm
Radius genau hindurchpasst.
Wie groß ist der Radius der Viertelkreise der Löcher?
![\includegraphics[width=4cm]{billard}](img12.png)
Zu Beginn liegt eine Kugel genau in der Mitte des Tisches; ansonsten ist der Tisch leer. Die Kugel wird langsam im 45o-Winkel zu den Seiten gestoßen.
In welches Loch wird die Kugel fallen, wenn die Reibung vernachlässigbar ist?
Lösung:
Wie gefordert berechnen wir zuerst die Größe der Löcher. Dazu hilft die
folgende Skizze:
![\includegraphics[width=35mm]{lochradius}](img13.png)
Aus Symmetriegründen berührt die Kugel, wenn sie im Loch steckt, den
Viertelkreisbogen des Loches genau auf der Winkelhalbierenden. Daher ist der
Radius rL des Loches die Summe des Radius der Kugel
rK = 5cm und
des Abstandes des Kugelmittelpunktes von der Ecke. Dieser Abstand ist
![]() . 5cm, also ist
rL = 5(1 +
. 5cm, also ist
rL = 5(1 + ![]() )cm
)cm ![]() 12, 071cm.
12, 071cm.
Beim zweiten Teil der Aufgabe konnte man sich an zwei Stellen vertun -
vielleicht war unsere Formulierung, was die zweite Stelle angeht, nicht
perfekt, dafür möchten wir dann um Entschuldigung bitten.
Die Kugel läuft auf ihrer Bahn natürlich genau so lange, bis sie die Bande berührt. Da sie einen Radius von 5 cm hat, ist ihr Mittelpunkt von der Bande dann noch 5 cm entfernt. Man kann sich die Bahn der Kugel also so vorstellen, dass der Mittelpunkt immer an den Rändern eines Rechtecks zurückgeworfen wird, dessen Kantenlängen in beiden Richtungen um 2 . 5 cm kürzer sind als die Längen des Billardtisches. (Das war der eine Fehler, der häufig vorkam. ,,Ausnahmsweise`` haben wir, obwohl Mathematiker das ja sonst gerne tun, nicht der Einfachheit halber mit einem nur punktförmigen Objekt rechnen wollen.) Dieses Rechteck sei effektives Rechteck genannt.
Die nächste Frage ist nun: Wann fällt die Kugel ins Loch? Nicht etwa nur
dann,
wenn sie sich dem Loch auf der Winkelhalbierenden der Ecke nähert. (Das war
der zweite Fehler.) Sondern
ganz allgemein dann, wenn ihr Auflagepunkt über den
Lochviertelkreis kommt. Dazu betrachten wir die Tangente an diesen Viertelkreis
im 45o-Winkel. Sie trifft auf das effektive Rechteck in einer Entfernung
von
![]() =
= ![]() . rK
. rK ![]() 7, 071cm von dessen Ecke. Die Kugel kann
den
Rand offenbar nur auf Punkten
erreichen, deren Koordinaten beide ganzzahlig sind, also fällt die Kugel genau
dann in ein Loch, wenn ihr Mittelpunkt maximal 7 cm entfernt von der
Ecke an den Rand des effektiven Rechtecks stößt.
7, 071cm von dessen Ecke. Die Kugel kann
den
Rand offenbar nur auf Punkten
erreichen, deren Koordinaten beide ganzzahlig sind, also fällt die Kugel genau
dann in ein Loch, wenn ihr Mittelpunkt maximal 7 cm entfernt von der
Ecke an den Rand des effektiven Rechtecks stößt.
![\includegraphics[width=35mm]{fallgrenze}](img16.png)
Jetzt können wir uns die genaue Bahn der Kugel ansehen, wobei wir nur im effektiven Rechteck rechnen, was ja nun eine Größe von 118 mal 78 Zentimetern hat. Den Nullpunkt legen wir nach links unten: Die Kugel startet dann beim Punkt (59, 39) und rollt zuerst nach rechts unten. Daher trifft sie beim Punkt (98, 0) auf die untere Bande, dann bei (118, 20) auf die rechte, bei (60, 78) auf die obere, bei (0, 18) auf die linke, bei (18, 0) wieder auf die untere Bande und weiter über die Bandenpunkte (96, 78), (118, 56), (62, 0), (0, 62), (16, 78) zum Punkt (94, 0) auf der unteren Bande. Bislang war kein Punkt nahe genug an einer Ecke dran. Der letzte Punkt ist genau 4 cm von dem ersten Berührpunkt entfernt und die Kugel rollt in dieselbe Richtung. Daher verschieben sich die anderen Berührpunkte auch um jeweils 4 cm.
![\includegraphics[width=80mm]{bahn1}](img17.png)
Beim Weiterzeichnen weiß man also schon, dass sich immer nur eine Koordinate gegenüber einer bereits bekannten um 4 verändert. Außerdem könnte man sich weiter überlegen, wo sich die Kugel im Laufe der weiteren Bahn einem Loch annähert und wo nicht und so zum Ergebnis kommen. Der Einfachheit halber listen wir hier weiter die Berührpunkte auf, bis ein Loch erreicht wird:
(94, 0), (118, 24), (64, 78), (0, 14), (14, 0), (92, 78), (118, 52), (66, 0), (0, 66), (12, 78), (90, 0) (wieder ist ein Rundgang vollendet), (118, 28), (68, 78), (0, 10), (10, 0), (88, 78), (118, 48), (70, 0), (0, 70), (8, 78), (86, 0) (noch ein Rundgang ohne Loch ...), (118, 32), (72, 78), (0, 6). Dieser Berührpunkt ist dicht genug am Loch dran, so dass die Kugel in Loch A fällt. (Man kann leicht nachrechnen, dass die Kugel wirklich auch noch die Bande berührt, denn der Viertelkreis schneidet die Seiten des effektiven Rechtecks des Kugelmittelpunktes in einem Abstand von etwa 5, 986 cm.)
![\includegraphics[width=80mm]{kugel_bahn}](img18.png)
In der Zeichnung ist gestrichelt auch noch der weitere Weg eingezeichnet, den die Kugel nehmen würde, wenn sie nur dann ins Loch fallen würde, wenn sie auf der Winkelhalbierenden ankommt. In diesem Fall würde sie ins Loch D fallen.
Man kann die Aufgabe auch etwas anders zeichnerisch lösen, dies sei hier nur
kurz skizziert: Das effektive Rechteck
kann man immer wieder an seinen Seiten spiegeln, so dass der Weg der
Kugel zu einer Geraden wird. Am besten macht man das so, dass auf Karopapier
eine Kästchenbreite in Wirklichkeit 4 Zentimetern entspricht, dann kann man
die Gerade
sehr leicht einzeichnen. Nun muss man noch entsprechend auf die Lochbereiche in
der Nähe der Geraden aufpassen - dabei muss man darauf achten, dass es keine
Vollkreise um einen Punkt sind, sondern dass die Bereiche von vier
Kreisbögen begrenzt werden, welche als Schnitt mit dem effektiven Rechteck
entstehen. Man muss
aber diese Bereiche nicht einzeichnen, es reicht, die Mittelpunkte der
Lochbereiche zu markieren und - wie oben berechnet - zu schauen, ob die
Gerade der Bahn der Kugel
waagerecht oder senkrecht den Abstand von 7 oder weniger Zentimetern
erreicht. Zum Schluss muss man noch, wenn man das nicht schon vorher getan hat,
zurückrechnen, welchem Loch der gestreifte Punkt denn entspricht.
Etwas zahlentheoretisch kann man diese Betrachtungsweise auch umformulieren zu
der Aufgabe: ,,Finde die kleinste positive ganze Zahl n mit der
Eigenschaft, dass 59 + n ein Vielfaches von 118 ist und dass 39 + n zu
einem Vielfachen von 78 eine Differenz von höchstens 7 hat.`` Dieses n
führt dann zur Lösung.
Aufgabe 4
Auf einem kreisrunden Erdbeerkuchen sind neben vielen Erdbeeren auch zwei (für unsere Rechnungen: punktförmige) Heidelbeeren zufällig verstreut.
- Der Kuchen wird in n gleiche Stücke geteilt, indem mit dem Messer von der Mitte des Kuchens n gerade Schnitte nach außen gemacht werden. Mit welcher Wahrscheinlichkeit sind dann die beiden Heidelbeeren auf demselben Stück?
- Nun wird der Kuchen durch die gleiche Art von Schnitten in n Stücke
zufälliger Größe geteilt. Man stelle sich zum Beispiel
vor, dass der Kuchen auf einem Drehtablett liegt und vor jedem Schnitt der
Kuchen zufällig irgendwie verdreht wird.
Mit welcher Wahrscheinlichkeit sind die beiden Heidelbeeren nun in demselben Stück?
Lösung:
Um uns die Vorstellung zu erleichtern, gehen wir davon aus, dass die Heidelbeeren erst nach dem Backen und nach dem Schneiden zufällig auf dem Kuchen verteilt werden, und zwar eine nach der anderen.
Dies dürfen wir tun, da das Schneiden der Stücke und das Verteilen der Beeren unabhängig voneinander geschehen.
Bei n Kuchenstücken gibt es für jede der beiden Beeren n verschiedene Möglichkeiten, auf welchem Stück sie landen können. Bei zwei Beeren macht das insgesamt n2 Möglichkeiten, die im Fall von identischen Stückgrößen auch alle gleichwahrscheinlich sind.
Da in genau n der n2 Fälle die beiden Beeren auf demselben Stück liegen, beträgt die Wahrscheinlichkeit p für dieses Ereignis gerade p = n2/n = 1/n.
Im zweiten Fall - hier ist die Größe der Kuchenstücke zufällig - gehen wir ein wenig anders an das Problem heran:
Wir ersetzen in Gedanken die Heidelbeeren durch (rote) Linien, die vom Kuchenmittelpunkt aus durch die jeweilige Heidelbeere bis zum Rand des Kuchens verlaufen. Zusammen mit den n eigentlichen (schwarzen) Schnitten haben wir nun n + 2 ,,Trennlinien``, die im Folgenden (gleichzeitig) zufällig auf dem Kuchen verteilt werden.
Nach dem Verteilen der Trennlinien nummerieren wir deren Positionen im Uhrzeigersinn, beginnend an der ,,12-Uhr-Position``.
Für dieses spezielle Winkelmuster gibt es nun
![]() =
= ![]() Möglichkeiten, wie sich die zwei roten Trennlinien auf die n + 2 Positionen
verteilen könnnen. Dabei sind alle dieser Möglichkeiten gleichwahrscheinlich.
Möglichkeiten, wie sich die zwei roten Trennlinien auf die n + 2 Positionen
verteilen könnnen. Dabei sind alle dieser Möglichkeiten gleichwahrscheinlich.
Bei genau n + 2 dieser Möglichkeiten liegen die beiden roten Trennlinien nebeneinander, was äquivalent dazu ist, dass die beiden Heidelbeeren auf demselben Stück liegen.
Dies gilt für jedes mögliche Winkelmuster.
Das heißt: Die Wahrscheinlichkeit für das gesuchte Ereignis beträgt
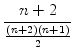 =
=
Variante:
Man kann die Aufgabe auch mithilfe der Integralrechnung lösen. Dazu gehen wir wieder noch etwas anders an die Aufgabe heran:
Wir gehen wie in der Aufgabenstellung davon aus, dass der Kuchen erst
geschnitten wird, nachdem die Heidelbeeren schon verteilt sind. Bevor wir
jedoch den ersten Schnitt machen, malen wir in Gedanken zwei Strecken auf den
Kuchen, die beide vom Mittelpunkt durch je eine Heidelbeere bis zum Rand des
Kuchens verlaufen. Diese trennen den Kuchen also in zwei Kreissektoren mit den
Winkeln ![]() und
und
![]() = 360o -
= 360o - ![]() auf.
auf.
Damit das Ereignis B : = {,, beide Beeren liegen auf demselben Stück``} eintritt, müssen alle n Schnitte, deren Position ja zufällig ist, entweder in dem einen oder in dem anderen der beiden gedachten Sektoren liegen.
Da ein einzelner Schnitt mit Wahrscheinlichkeit
![]() /360o in den
ersten und mit Wahrscheinlichkeit
/360o in den
ersten und mit Wahrscheinlichkeit
![]() /360o in den zweiten Sektor
fällt, beträgt die Wahrscheinlichkeit für das Ereignis B für einen festen
Winkel
/360o in den zweiten Sektor
fällt, beträgt die Wahrscheinlichkeit für das Ereignis B für einen festen
Winkel
![]() = :
= : ![]()
Approximativ können wir
![]() (B) nun berechnen, indem wir uns
vorstellen,
(B) nun berechnen, indem wir uns
vorstellen, ![]() würde nur ganzzahlige Winkel von 1o bis
360o annehmen, und zwar jeden davon mit derselben Wahrscheinlichkeit
p
würde nur ganzzahlige Winkel von 1o bis
360o annehmen, und zwar jeden davon mit derselben Wahrscheinlichkeit
p![]() =
= ![]() .
Dann würden wir alle
B
.
Dann würden wir alle
B![]() , jeweils gewichtet mit der
Wahrscheinlichkeit
p
, jeweils gewichtet mit der
Wahrscheinlichkeit
p![]() =
= ![]() , aufsummieren und erhielten so
die gesuchte Wahrscheinlichkeit
, aufsummieren und erhielten so
die gesuchte Wahrscheinlichkeit
Da aber ![]() nicht nur diese endlich vielen Werte annehmen muss, sondern
jeden Wert aus dem Intervall
[0o, 360o] annehmen
kann, müssen wir - um das exakte Ergebnis zu erhalten - über den Ausdruck,
über den wir eben summiert haben, integrieren:
nicht nur diese endlich vielen Werte annehmen muss, sondern
jeden Wert aus dem Intervall
[0o, 360o] annehmen
kann, müssen wir - um das exakte Ergebnis zu erhalten - über den Ausdruck,
über den wir eben summiert haben, integrieren:
| = |
||
| = |
||
| = |
Verallgemeinerung:
Der erste Lösungsansatz lässt sich bequem auf m zu verteilende Heidelbeeren verallgemeinern:
Es gibt
![]() Möglichkeiten, die m Heidelbeeren auf die n + m
Positionen zu verteilen; bei n + m davon liegen alle Heidelbeeren auf demselben
Stück.
Möglichkeiten, die m Heidelbeeren auf die n + m
Positionen zu verteilen; bei n + m davon liegen alle Heidelbeeren auf demselben
Stück.
Also beträgt die Wahrscheinlichkeit für ebendieses Ereignis
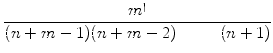 .
.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File

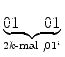 .
.