Beispiellösungen zu Aufgabenblatt 66

aktualisiert: 14. Januar 2008

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File

Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.

Aufgabe 1

Zehn Schüler nahmen an einem Mathewettbewerb teil. Jede Aufgabe wurde von genau sieben Schülern gelöst. Neun der zehn Schüler lösten jeweils genau vier Aufgaben.

Wie viele Aufgaben hat der zehnte Schüler gelöst?

Lösung:

Sei a die Anzahl der Aufgaben im Wettbewerb und sei x die Anzahl der Aufgaben, die der zehnte Schüler gelöst hat.

Da der zehnte Schüler nicht mehr Aufgaben gelöst haben kann, als gestellt wurden, gilt:

0 $\displaystyle \leq$ x $\displaystyle \leq$ a.

(1)

Alle zehn Schüler zusammen haben 9^.4 + x Aufgaben gelöst. Außerdem wurde jede Aufgabe von genau 7 Schülern gelöst. Deswegen gilt:

9^.4 + x = 7^.a.

(2)

Unter Benutzung von (

) folgt

36 $\displaystyle \leq$ 36 + x	= 7^.a $\displaystyle \Longrightarrow$ 5 $\displaystyle {\frac{{1}}{{7}}}$ = $\displaystyle {\frac{{36}}{{7}}}$ $\displaystyle \leq$ a
und 36 + a $\displaystyle \geq$ 36 + x	= 7^.a $\displaystyle \Longrightarrow$ 36 $\displaystyle \geq$ 6^.a bzw. 6 $\displaystyle \geq$ a.

Wir erhalten schließlich a = 6 und damit x = 7^.6 - 36 = 6.

Probe: Einsetzen von x = 6 und a = 6 in () und () ergibt wahre Aussagen. Der zehnte Schüler muss somit tatsächlich sechs Aufgaben gelöst haben.

Man kann sich noch überlegen, dass eine solche Verteilung der 42 Aufgaben auf die zehn Schüler auch praktisch möglich ist. Eine mögliche Verteilung ist in der folgenden Tabelle dargestellt:

	Teilnehmernummer
	1	2	3	4	5	6	7	8	9	10
Aufgabe
1	x	x	x	x	x	x				x
2	x	x	x	x	x	x				x
3	x	x	x				x	x	x	x
4	x	x	x				x	x	x	x
5				x	x	x	x	x	x	x
6				x	x	x	x	x	x	x

Aufgabe 2

Für eine bevorstehende große Seeschlacht hat Käpt'n Jakob Sperling 5100 frische Kanonenkugeln besorgt. Davon sind 5000 Stück für die ,,Dicke Bertha`` und 100 Stück für die praktische kleine Handkanone ,,Flotte Lotte``. Seine Jungs können es nun nicht lassen und spielen verbotenerweise mit einer zufällig ausgewählten Kugel Bowling auf dem Deck. Dabei wird die Kugel so lädiert, dass sie nicht mehr geradeaus fliegen wird. Die Crew versucht den ,,Unfall`` zu vertuschen und legt die beschädigte Kugel einfach wieder zu den anderen. Käpt'n Jakob Sperling merkt jedoch natürlich sofort, dass etwas faul ist, und befragt seine Mannschaft. Einer der Piraten behauptet, sie hätten mit einer großen Kugel für die ,,Dicke Bertha`` gespielt. Der Pirat ist trotz der Unterrichtsstunde im Lügen leider noch kein Profi, denn er lügt bei solchen Angelegenheiten nur in 95 Prozent aller Fälle.

Wie groß ist die Wahrscheinlichkeit, dass die Mannschaft tatsächlich mit einer Kugel der ,,Dicken Bertha`` gespielt hat?

Lösung:

Wenn man betrachtet, mit welcher Kugel gespielt worden sein kann und ob der befragte Pirat ehrlich ist, so ergeben sich die folgenden vier Fälle:

Die Kugel ist für die ,,Dicke Bertha`` und der Pirat sagt die Wahrheit.
Die Kugel ist für die ,,Dicke Bertha`` und der Pirat lügt.
Die Kugel ist für die ,,Flotte Lotte`` und der Pirat sagt die Wahrheit.
Die Kugel ist für die ,,Flotte Lotte`` und der Pirat lügt.

Die Wahrscheinlichkeit, dass die Mannschaft mit einer Kugel für die ,,Dicke Bertha`` bzw. die ,,Flotte Lotte `` gespielt hat (unabhängig von der Aussage des Piraten), beträgt ${\frac{{5000}}{{5100}}}$ = ${\frac{{50}}{{51}}}$ bzw. ${\frac{{100}}{{5100}}}$ = ${\frac{{1}}{{51}}}$ .
Die Wahrscheinlichkeit, dass der Pirat lügt bzw. die Wahrheit sagt, ist 95% bzw. 5%.

Weil wir nun die Aussage des Piraten kennen, bilden der erste und der vierte Fall unsere neue Grundgesamtheit, sind also zusammen 100 %. Der zweite und der dritte Fall fallen weg.

Der erste Fall hat die Wahrscheinlichkeit ${\frac{{50}}{{51}}}$ ^. ${\frac{{5}}{{100}}}$ = ${\frac{{5}}{{102}}}$ und die Wahrscheinlichkeit des vierten Falls beträgt ${\frac{{1}}{{51}}}$ ^. ${\frac{{95}}{{100}}}$ = ${\frac{{19}}{{1020}}}$ .

Die gesuchte Wahrscheinlichkeit p ist dann die Wahrscheinlichkeit, dass der erste Fall innerhalb dieser Grundgesamtheit auftritt, also

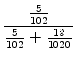p = $\displaystyle {\frac{{\frac{5}{102}}}{{\frac{5}{102} + \frac{19}{1020}}}}$ = $\displaystyle {\frac{{50}}{{69}}}$ $\displaystyle \approx$ 72, 5%.

Aufgabe 3

Das Polynom P(x) = x² + x³ + x⁵ +...+ x⁹⁷ enthält als Summanden alle x-Potenzen mit Primzahlexponenten, die kleiner als 100 sind. Jemand berechnet das Polynom

Q(x) = P(x)⁴ = a₃₈₈x³⁸⁸ + a₃₈₇x³⁸⁷ + a₃₈₆x³⁸⁶ +...+ a₁x + a₀.

Was ist dann der Wert der Summe a₀ + a₂ + a₄ +...+ a₃₈₆ + a₃₈₈ der Koeffizienten mit geradem Index?

Lösung:

Es gibt genau 25 Primzahlen, die kleiner sind als 100. Dies sind: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 und 97. (Die Zahlen sind hier nur der Vollständigkeit halber aufgeführt und werden zur Lösung der Aufgabe nicht benötigt.)

Nun betrachten wir den Ausdruck P(x)⁴, jedoch ohne dabei die Summanden mit gleichem Exponenten zusammenzufassen. P(x)⁴ ist dann eine Summe von 25⁴ Potenzen von x, deren Exponent jeweils eine Summe von vier Primzahlen ist. Da die Koeffizienten im Polynom P(x) alle 1 sind und wir die Potenzen nicht zusammengefasst haben, hat auch jeder der 25⁴ Summanden in P(x)⁴ den Koeffizient 1.

Jetzt müssen wir nur noch die Summanden mit geradem Exponenten zählen:

Die einzige gerade Primzahl ist die 2; deshalb ist der Exponent eines Summanden genau dann gerade, wenn im Exponenten

alle 4 Summanden ungleich 2 sind,
genau 2 Summanden gleich 2 sind oder wenn
alle 4 Summanden gleich 2 sind.

Vom ersten Typ gibt es 24⁴ Summanden, vom zweiten Typ 6^.24² (man muss betrachten, aus welchen zwei der vier Faktoren die beiden Exponenten 2 stammen: dafür gibt es genau 6 Möglichkeiten) und vom dritten Typ gibt es genau einen Summanden.

Die Summe der Koeffizienten mit geradem Index beträgt also

24⁴ + 6^.24² + 1 = 335233.

Bemerkung: In der ursprünglichen Formulierung der Aufgabe war versehentlich nur die Summe a₀ + a₂ + a₄ +...+ a₃₈₆ gesucht. Wegen a₃₈₈ = 1 hat diese dann den Wert 335 232.

Lösungsvariante:

Durch Einsetzen der Werte 1 und -1 in das Polynom Q(x) erhält man mit

$\displaystyle {\frac{{1}}{{2}}}$ (Q(1) + Q(- 1))	= $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \left(\vphantom{ a_{388} + a_{387} + \ldots + a_1 + a_0 }\right.$ a₃₈₈ + a₃₈₇ +...+ a₁ + a₀
	+ $\displaystyle \left.\vphantom{ (a_{388} - a_{387} + a_{386} - a_{385} \pm \ldots - a_1 + a_0) }\right.$ (a₃₈₈ - a₃₈₇ + a₃₈₆ - a₃₈₅±...- a₁ + a₀) $\displaystyle \left.\vphantom{ (a_{388} - a_{387} + a_{386} - a_{385} \pm \ldots - a_1 + a_0) }\right)$
	= a₃₈₈ + a₃₈₆ +...+ a₂ + a₀

die gesuchte Summe der Koeffizienten mit geradem Index.

Andererseits ist aber

$\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \left(\vphantom{ Q(1) + Q(-1) }\right.$ Q(1) + Q(- 1) $\displaystyle \left.\vphantom{ Q(1) + Q(-1) }\right)$	= $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \left(\vphantom{ P(1)^4 + P(-1)^4}\right.$ P(1)⁴ + P(- 1)⁴ $\displaystyle \left.\vphantom{ P(1)^4 + P(-1)^4}\right)$
	= $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \left(\vphantom{ 25^4 + (1 - 24)^4 }\right.$ 25⁴ + (1 - 24)⁴ $\displaystyle \left.\vphantom{ 25^4 + (1 - 24)^4 }\right)$ = 335233.

Also gilt a₃₈₈ + a₃₈₆ +...+ a₂ + a₀ = 335233.

Aufgabe 4

Ein regelmäßiges Sechseck ,,rollt`` entlang einer Geraden, indem es fortlaufend über die rechte der beiden auf der Geraden liegenden Ecken gekippt wird. Zu Beginn ist die Position der linken unteren Ecke des Sechsecks markiert. Nach jeder Kippung wird wieder die Position dieser Ecke markiert. Nach fünf solcher Kippungen berührt die betrachtete Ecke zum ersten Mal wieder die Gerade.

$\includegraphics[width=10cm]{sechseck}$

Zeige, dass das Flächenstück, das durch die markierten Punkte und die Gerade begrenzt ist, genau dreimal so groß ist wie die Fläche des Sechsecks.

Wie ist das Verhältnis der entsprechenden Flächen bei anderen regelmäßigen n-Ecken? Behandle zunächst die Fälle n = 3 und n = 4, stelle dann eine Vermutung auf und versuche, diese zu beweisen.

Lösung:

Bei der Sechseckfigur sind ja bereits die Secheckumrisse zu sehen. Wenn man die Figur noch weiter zu einem Muster aus gleichseitigen Dreiecken ergänzt, kann man diese Dreiecke einfach abzählen. Vier Dreiecke sind dabei genau halbiert, sie ergänzen sich also zu zwei vollen Dreiecken.

$\includegraphics[width=10cm]{sechseck_loes}$

Im Ergebnis ist die markierte Fläche so groß wie 18 Dreiecke, während das regelmäßige Sechseck aus sechs gleichseitigen Dreiecken besteht. Wie behauptet, ist das Flächenstück also genau dreimal so groß wie das Sechseck.

Für ein Drei- oder Viereck lässt sich die Aufgabe auf entsprechende Weise lösen, sogar noch einfacher:

$\includegraphics[width=12cm]{drei_und_viereck_loes}$

Beim Dreieck setzt sich das gegebene Flächenstück aus sechs rechtwinkligen, ,,halben gleichseitigen`` Dreiecken zusammen und ist damit ebenfalls dreimal so groß wie ein gleichseitiges Dreieck.

Am einfachsten ist wohl die Lösung beim Viereck: Die beiden Dreiecke an den Enden ergänzen sich genau zu einem Quadrat, also ist auch hier die markierte Fläche dreimal so groß wie das erzeugende 4-Eck.

Die nun nicht mehr überraschende Vermutung lautet also:

Für jedes regelmäßige n-Eck ist die sich ergebende Figur genau dreimal so groß wie das n-Eck.

Beweis, dass dies stimmt: Wir betrachten zunächst nur das n-Eck mit seinem markierten Punkt (der in der Skizze - mit n = 7 - bereits links unten liegt). Von diesem Punkt aus zeichnen wir alle Diagonalen in das n-Eck und unterteilen es so in n - 2 Dreiecke.

$\includegraphics[width=35mm]{n_eck_geteilt}$

Beim Abrollen des n-Ecks wie beschrieben lassen wir nun nach dem ersten Kippen das erste der Dreiecke quasi liegen (das heißt, färben den entsprechenden Bereich in der Figur), nach dem zweiten Kippen das zweite usw. bis nach dem vorletzten Kippen. (Nach dem letzten Kippen gibt es kein Dreieck mehr, das macht aber nichts.)

Es ergibt sich folgendes Bild:

$\includegraphics[width=130mm]{sieben_loes}$

Der Flächeninhalt aller gefärbten Teile ist also genau die Fläche des n-Ecks.

Die übrig bleibende Fläche besteht aus n - 1 weißen Dreiecken.

Nun stellen wir fest, dass ein weißes Dreieck zusammen mit den beiden benachbarten gefärbten Dreiecken ein Trapez bildet:

$\includegraphics[width=70mm]{trapez}$

Begründung: Die Strecke a ist eine Diagonale (ggf. auch Kante) in einer Kopie des n-Ecks; in der nächsten Kopie des n-Ecks ist sie mit a' bezeichnet. Die Strecke b ist eine zu a', also auch zu a parallele Diagonale, weil sie die beiden Eckpunkte verbindet, die den Eckpunkten von a' zur selben Seite hin benachbart sind.

Die Streckenstücke auf der Grundseite der Figur sind alle gleich lang, weshalb die untere Spitze des weißen Dreiecks die Seite des Trapezes halbiert. Wenn mit m die Mittellinie des Trapezes bezeichnet ist, die gleichzeitig Seitenhalbierende des weißen Dreiecks ist, hat das weiße Dreieck die Fläche m^.h. Außerdem ist m als Mittellinie des Trapezes gerade das arithmetische Mittel der Seitenlängen a und b. Die gefärbten Dreiecke haben in der Summe also den Flächeninhalt ${\frac{{1}}{{2}}}$ ah + ${\frac{{1}}{{2}}}$ bh = mh. Daher ist ein weißes Dreieck genauso groß wie die beiden angrenzenden gefärbten Dreiecke zusammen. Das gilt auch am Rand, wo man ein zu einem Dreieck entartetes Trapez und nur ein gefärbtes Dreieck hat.

Addiert man alles, ergibt sich: Die weißen Dreiecke haben in der Summe einen Flächeninhalt wie zweimal die gefärbten Dreiecke, also zweimal die Fläche des n-Ecks. Insgesamt hat demnach die Figur wie behauptet den dreifachen Flächeninhalt des n-Ecks.

Bemerkungen: Da man die gefärbten Dreiecke nach Konstruktion aneinanderfügen kann, sind die noch ungefärbten Dreiecke gleichschenklig. Weil die Spitze des Dreiecks auf der Mitte der einen Trapezseite liegt, folgt aus der Gleichschenkligkeit, dass das Trapez auf der anderen Seite rechte Winkel haben muss.

Alternativlösung:
Die Aufgabe lässt sich auch ,,durchrechnen``, unter mehrfacher Zuhilfenahme von Additionstheoremen der trigonometrischen Funktionen. Mit diesem aufwändigen Beweis (den wir vor der gezeigten elementargeometrischen Variante gefunden hatten) wollten wir die Leser der Beispiellösungen nicht verschrecken; aber wer daran interessiert ist, kann ihn sich hier ansehen.

$drucken$ Zum Ausdrucken als pdf-File oder als ps-File