 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
Leider führte das automatische Konvertieren in das HTML-Format zu einigen Darstellungsfehlern, die wir nicht beheben können. Die HTML-Darstellung auf dieser Seite ist daher nur im nicht formelhaltigen Text korrekt und somit nur für einen Überblick über die Lösungen geeignet. Für korrekte Formeln und Bilder verweisen wir auf die PDF- oder PS-Version - und bitten um Verständnis.
Aufgabe 1
Finde alle natürlichen Zahlen n, für die
![]() eine natürliche Zahl ergibt.
eine natürliche Zahl ergibt.
Sei allgemeiner k eine natürliche Zahl - bestimme analog die Menge aller
natürlichen Zahlen n, für die
![]() eine natürliche
Zahl ist.
eine natürliche
Zahl ist.
Lösung:
Wir betrachten gleich den allgemeinen Fall mit einer natürlichen Zahl k. Die
an die gesuchte natürliche Zahl n gestellte Bedingung, dass auch
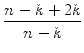 =
= Aus dem ersten Fall folgt - (n - k) = 2k, also - n = k. In natürlichen Zahlen hat das genau eine Lösung: n = k = 0. Da dann jedoch der Nenner n - k auch null wäre, ist dies keine Lösung der Aufgabe.
Also ist
![]() eine natürliche Zahl. Weil der
Zähler 2k nach Voraussetzung nichtnegativ ist, ist dies genau dann der
Fall, wenn m : = n - k ein positiver2 Teiler von 2k ist.
eine natürliche Zahl. Weil der
Zähler 2k nach Voraussetzung nichtnegativ ist, ist dies genau dann der
Fall, wenn m : = n - k ein positiver2 Teiler von 2k ist.
Also sind die Lösungen des Problems alle
n ![]()
![]() , die sich in der
Form n = m + k schreiben lassen, wobei für m jeder positive Teiler von 2k
gewählt werden kann.
, die sich in der
Form n = m + k schreiben lassen, wobei für m jeder positive Teiler von 2k
gewählt werden kann.
Für k = 0 bedeutet das übrigens, dass jede natürliche Zahl n ungleich null
eine Lösung ist, wie man auch sofort am Bruch
![]() =
= ![]() = 1 sieht.
= 1 sieht.
Im Spezialfall k = 9 wiederum bedeutet dies, dass n - 9 ein Teiler von 18 sein muss, also eine der Zahlen 1, 2, 3, 6, 9, 18. Somit ergeben sich die Lösungen:
| n | 10 | 11 | 12 | 15 | 18 | 27 |
| n - 9 | 1 | 2 | 3 | 6 | 9 | 18 |
|
|
19 | 10 | 7 | 4 | 3 | 2 |
Aufgabe 2
Zeige, dass die ,,Jahreswechselzahl``
Lösung:
Wir formen die Jahreswechselzahl geschickt um und erhalten:
| 111...11 | 222...225 = 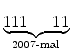 . 102009 + 2 . . 102009 + 2 . 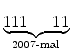 . 102 + 25 . 102 + 25 |
|
= 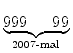 . 102009 + 2 . . 102009 + 2 . 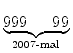 . 102 + 25 . 9 . 102 + 25 . 9 |
||
| = |
||
| = |
||
| = |
||
| = |
||
| = |
||
| = |
||
= 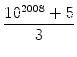 |
Die Jahreswechselzahl ist also genau dann eine Quadratzahl, wenn
![]() eine natürliche Zahl, d. h. falls
102008 + 5 durch 3 teilbar ist.
eine natürliche Zahl, d. h. falls
102008 + 5 durch 3 teilbar ist.
Da die Quersumme Q(102008 + 5) = 1 + 5 = 6 durch 3 teilbar ist, ist auch die Zahl 102008 + 5 selbst durch 3 teilbar. Man sieht die Teilbarkeit aber auch der Zahl direkt an, denn es gilt
= 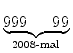 + 1 + 5 + 1 + 5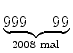 + 6 + 6 |
||
= 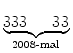 + 2 = + 2 = 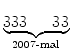 5. 5. |
Die Jahreswechselzahl ist damit die Quadratzahl
111...11222...225 = 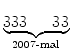 5 5 |
Aufgabe 3
Die Crew um Käpt'n Sperling kreuzt im Nordmeer herum. Einige Schiffe werden
gesichtet, doch der Chef bläst nie zum Angriff, was die Crew wundert. Darauf
angesprochen, erklärt Sperling: ,,Seht ihr das hell erleuchtete Haus da
hinten auf der Insel? Das ist das Haus vom Nikolaus. Und die meisten Schiffe
hier liefern ihm Nachschub für die Weihnachtsgeschenke, bei denen er
dem Weihnachtsmann hilft. Ehrensache, dass wir die nicht plündern! Die Schiffe
erkennt man übrigens an einem speziellen Flaggentyp: Auf ihr ist ein
Streckenzug, dessen einzelne Strecken in der gegebenen Reihenfolge Längen
haben, wie sie auch auftreten können, wenn man das bekannte ,Haus vom
Nikolaus` zeichnet.``
Ein Beispiel für einen Streckenzug, der auf einer echten Flagge abgebildet sein könnte, ist der folgende:
Welche der folgenden Flaggen sind echt, welche sind Fälschungen?
![\includegraphics[width=0.97\textwidth]{nikolausflaggen1}](img45.png)
![\includegraphics[width=0.97\textwidth]{nikolausflaggen2}](img46.png)
Lösung:
Die Flaggen 1, 4, 6 und 8 sind Originale, die Flaggen 2, 3, 5 und 7 hingegen
Fälschungen.
Zunächst geben wir für die vier Originale je eine Möglichkeit an, aus dem gegebenen Streckenzug das Haus vom Nikolaus zu zeichnen:
![\includegraphics[width=130mm]{haeuser}](img48.png)
Betrachten wir nun die mutmaßlichen Fälschungen:
Flagge 2: Diese Flagge muss eine Fälschung sein, da man die beiden langen Diagonalen beim Haus vom Nikolaus nicht direkt nacheinander zeichnen kann.
Flagge 3: Da das Haus vom Nikolaus bekanntlich aus genau acht Geradenstücken besteht, dieser Streckenzug aber neun Teile hat, ist auch Flagge 3 eine Fälschung.
Flagge 5: Grundsätzlich gilt: Zeichnet man einen Graphen wie das Haus vom Nikolaus in einem zusammenhängenden Streckenzug und ist einer der Punkte des Graphen weder Anfangs- noch Endpunkt, dann geht von ihm eine gerade Anzahl an Strecken aus. Denn bei jedem ,,Durchlauf`` des Streckenzuges wird eine Strecke zum Ankommen und eine zum Wegbewegen gebraucht; insgesamt gibt es dann also immer zueinandergehörende Paare von Strecken.3
Im Haus vom Nikolaus laufen nun in den beiden unteren Punkten eine ungerade Anzahl von Kanten zusammen. Daher müssen diese beiden Punkte Anfangs- und Endpunkt des Streckenzuges sein. Insbesondere darf also das Dach (bestehend aus den beiden kurzen Diagonalen) nicht am Ende des Streckenzuges sein. Damit ist auch diese Fälschung enttarnt.
Flagge 7: In einem Originalstreckenzug, bei dem eine lange Diagonale direkt am Dach (bestehend aus den beiden kurzen Diagonalen) anschließt, darf zwischen Dach und der zweiten langen Diagonalen nur eine gerade Anzahl von Stücken der Länge 1 liegen. Ansonsten würde die zweite Diagonale in einer Ecke starten, auf welche auch schon die erste Diagonale trifft.
Daher kann schließlich Flagge 7 ebenso kein Original sein.
Aufgabe 4
Die Funktion f habe die Eigenschaft
| f (x) - f (y)| ![]() | x - y|2 für alle
reellen Zahlen x, y. Zeige, dass f eine konstante Funktion ist.
| x - y|2 für alle
reellen Zahlen x, y. Zeige, dass f eine konstante Funktion ist.
Lösung:
Wir benutzen die sogenannte Dreiecksungleichung:
Für alle reellen Zahlen a und b gilt
| | a + b| |
Für alle, die diese in sehr vielen Fällen nützliche Ungleichung nicht kennen, folgt unten ein Beweis.
Seien nun x, y reelle Zahlen.
(Für die Vorstellung reicht es, an x < = y zu denken - für die Rechnung
ist es unerheblich.)
Sei weiterhin n eine positive ganze Zahl.
Dann gilt:
| | | 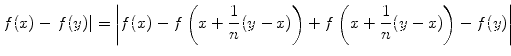 |
|
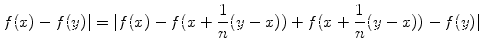 |
||
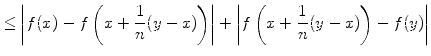 |
||
nach der Dreiecksungleichung | ||
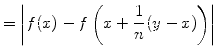 |
||
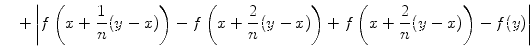 |
||
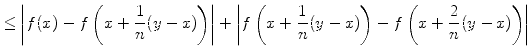 |
||
 |
||
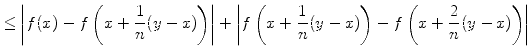 |
||
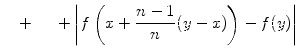 |
||
Wir haben nun n Summanden der Form
mit k
| - |
||
| = |
Also erhält man
| = n . |
Für feste x und y sowie wachsendes n wird der Term auf der rechten Seite der Ungleichung immer kleiner, nämlich kleiner als jede Zahl größer null. Somit muss
Beweis der Dreiecksungleichung:
Wir unterscheiden, ob die Summe a + b positiv oder nichtnegativ ist, und
benutzen jeweils, dass
x ![]() | x| gilt - unabhängig davon, ob die reelle
Zahl x negativ, null oder positiv ist.
| x| gilt - unabhängig davon, ob die reelle
Zahl x negativ, null oder positiv ist.
Fall I: Sei a + b > 0.
Dann ist
| a + b| = a + b ![]() | a| + | b|.
| a| + | b|.
Fall II: Sei
a + b ![]() 0.
0.
Dann ist
| a + b| = - (a + b) = (- a) + (- b) ![]() | a| + | b|.
| a| + | b|.
Alternative Lösung: Für Leser, die mit der Differentialrechnung
vertraut sind, folgt nun noch eine weitere kurze Beweisvariante: Für x ![]() y
kann man die gegebene Ungleichung durch | x - y| dividieren und sieht, dass gilt:
y
kann man die gegebene Ungleichung durch | x - y| dividieren und sieht, dass gilt:
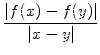
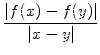
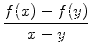 = 0.
= 0.
Fußnoten
- ... (meistens)1
- Über die Frage, ob Null eine natürliche Zahl ist, kann man sich hervorragend streiten, wenn man will ... Wir hoffen, richtig beobachtet zu haben, dass in der Schule in der Regel Null eine natürliche Zahl ist.
- ... positiver2
- Die Einschränkung auf positive
Teiler ist für 2k = 0 nötig, da 0 zwar ein Teiler von 0 ist, weil es - so
die Definition - eine positive ganze Zahl j mit
0 = j . 0 gibt (das
geht hier natürlich für alle positiven ganzen j), aber
,,
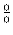 `` keine natürliche Zahl ist.
`` keine natürliche Zahl ist.
- ... Strecken.3
- Die Umkehrung dieser Aussage ist im Allgemeinen nicht richtig: Zum Beispiel ist bei einem Quadrat jeder Anfangspunkt eines durchgehenden Streckenzuges natürlich an einem Punkt mit gerader Anzahl an Kanten.
 Zum Ausdrucken als pdf-File
oder als ps-File
Zum Ausdrucken als pdf-File
oder als ps-File
